Politechnika Opolska
Wydział Elektrotechniki, Automatyki i Informatyki

Ekonometria
Kierunek studiów: Informatyka Prowadzący:
Rok akademicki: 2014/2015 dr inż. Arkadiusz Gardecki
Semestr: I Adam Czech
Cel projektu
Celem projektu jest stworzenie programu, który z podanych danych statycznych wspomoże budowę jednorównaniowego modelu ekonometrycznego. Program ten ma w łatwy i przystępny, z punku widzenia użytkownika, realizować obliczenia z danych zawartych w pliku tekstowym.
Dane statystyczne
Dane statyczne umieszczone w pliku tekstowym:
Tabela 1 Dane statystyczne wykorzystane w modelu
|
Lp. |
Rok |
Liczba emigracji (w tys.) |
Bezrobocie (w tys.) |
Zarobki (w PLN) |
Populacji (w tys.) |
PKB (w mln.) |
|
Y |
X1 |
X2 |
X3 |
X4 |
||
|
1 |
2003 |
786 |
3176 |
800 |
38191 |
103,4 |
|
2 |
2004 |
1000 |
3000 |
824 |
38174 |
105,1 |
|
3 |
2005 |
1450 |
2773 |
849 |
38157 |
103,5 |
|
4 |
2006 |
1950 |
2309 |
899 |
38125 |
106,2 |
|
5 |
2007 |
2270 |
1747 |
934 |
38116 |
107,2 |
|
6 |
2008 |
2210 |
1474 |
1126 |
38136 |
103,9 |
|
7 |
2009 |
2100 |
1893 |
1276 |
38167 |
102,6 |
|
8 |
2010 |
2000 |
1955 |
1317 |
38530 |
103,7 |
|
9 |
2011 |
2060 |
1983 |
1386 |
38538 |
104,8 |
|
10 |
2012 |
2130 |
2137 |
1500 |
38533 |
101,8 |
|
11 |
2013 |
2196 |
2158 |
1600 |
38496 |
101,7 |
Gdzie:
Y – Ilość ludzi
na emigracji w tysiącach,
X1 - Ilość zarejestrowanych
bezrobotnych w tysiącach,
X2 – Średnie wynagrodzenie brutto
w złotówkach,
X3 – Ilość mieszkańców w kraju,
X4 -
PKB (Przychód Krajowy Brutto) w milionach.
Współczynniki korelacji
Liczba określająca w jakim stopniu zmienne są współzależne. Jest to miara korelacji
Między zmienną objaśnianą Y i zmiennymi objaśniającymi Xi. Ocena ta została wykonan przy pomocy wzoru na ri. Do obliczenia wykorzystano wzór:
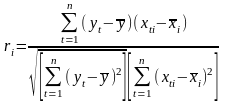
Po obliczeniu poszczególnych współczynników korelacji otrzymano R0:
|
R0 |
-0,9502 |
|
0,6572 |
|
|
0,2549 |
|
|
0,0913 |
W następnej kolejności obliczone zostały współczynniki korelacji między potencjalnymi zmiennymi objaśniającymi. Aby tego dokonać wykorzystano wzór:
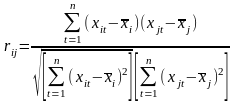

Po podstawieniu odpowiednich elementów do wzoru otrzymano macierz współczynników korelacji R:
|
R |
1 |
-0,6135 |
-0,1838 |
-0,0919 |
|
-0,6135 |
1 |
0,7995 |
-0,4987 |
|
|
-0,1838 |
0,7995 |
1 |
-0,4003 |
|
|
-0,0919 |
-0,4987 |
-0,4003 |
1 |
Wybór zmiennych objaśniających
Do wyboru zmiennych wyjaśniających posłuży metoda współczynników korelacji wielorakiej dla poziomu istotności α=0,1.
Metoda Z. Pawłowskiego jest to metoda doboru zmiennych objaśniających do modelu statystycznego w szczególności modelu ekonometrycznego.
Aby dokonać wyboru zmiennych w pierwszej kolejności budujemy tzw. macierz rozszerzoną W:
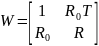
gdzie:
W – pełną macierzą korelacji
Macierze R oraz W wykorzystujemy do budowy współczynnika korelacji wielorakiej Ci, który jest miarą liniowej zależności między zmienną objaśnianą a liniową kombinacją zmiennych objaśniających.
Obliczony jest ze wzoru:
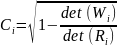
Oszacowanie parametrów strukturalnych modelu
Stosując Metodę Najmniejszych Kwadratów oszacowano parametry strukturalne modelu, oszacowanie to odbyło się po wybraniu zmiennych objaśniających.
Wzór ogólny tego modelu to:
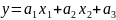
Wyznaczenie parametrów ai, było możliwe dzięki wzorowi:
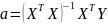
Aby skorzystać z wzoru potrzebne było wyznaczenie macierzy X oraz Y. Macierz X sprowadza się do wybrania kolumn reprezentujących wartości zmiennych X1, X2 z tabeli z danymi oraz dopisanie do niej kolumny jednostkowej, czyli kolumny samych jedynek. Macierz Y to tak naprawdę wartości zmiennej Y z tabeli danych statystycznych:
|
Y =
|
786 |
|
|
|
||
|
1000 |
|
|
|
|||
|
1450 |
|
|
|
|||
|
1950 |
|
|
|
|||
|
2270 |
|
|
|
|||
|
2210 |
|
|
|
|||
|
2100 |
|
|
|
|||
|
2000 |
|
|
|
|||
|
2060 |
|
|
|
|||
|
2130 |
|
|
|
|||
|
|
|
|
|
|
||
|
|
X = |
3176 |
800 |
1 |
||
|
|
3000 |
824 |
1 |
|||
|
|
2773 |
849 |
1 |
|||
|
|
2309 |
899 |
1 |
|||
|
|
1747 |
934 |
1 |
|||
|
|
1474 |
1126 |
1 |
|||
|
|
1893 |
1276 |
1 |
|||
|
|
1955 |
1317 |
1 |
|||
|
|
1983 |
1386 |
1 |
|||
|
|
2137 |
1500 |
1 |
|||
Posiadając już macierz Y i X wyznaczono współczynniki a1, a2 i a3. Następnym etapem jest wyznaczenie macierzy transponowanej XT:
|
XT= |
786 |
1000 |
1450 |
1950 |
2270 |
2210 |
2100 |
2000 |
2060 |
2130 |
|
3176 |
3000 |
2773 |
2309 |
1747 |
1474 |
1893 |
1955 |
1983 |
2137 |
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Otrzymaną macierz XT pomnożono przez macierz X w wyniku czego otrzymano macierz XTX:
|
XTX = |
53237203 |
23678431 |
22447 |
|
23678431 |
12521871 |
10911 |
|
|
22447 |
10911 |
10 |
Otrzymaną macierz odwrócono i pomnożono przez iloczyn macierzy XT i Y :
|
(XTX)-1= |
0 |
0 |
-0,002 |
|
0 |
0 |
-0,005 |
|
|
-0,002 |
-0,005 |
9,663 |
|
XTY= |
0 |
0 |
-0,0021 |
|
0 |
0 |
-0,0045 |
|
|
-0,0021 |
-0,0045 |
9,6627 |
|
|
|
|
|
|
Po wykonaniu wszystkich tych operacji otrzymujemy macierz a:
|
a= |
0 |
0 |
-0.0193254 |
|
0 |
0 |
-0.0483135 |
|
|
-0.0202923 |
0.0434835 |
93.3706968 |
Gdy otrzymaną macierz a podstawimy do ogólnego wzoru opisującego model otrzymujemy:
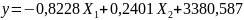
Weryfikacja modelu
Aby dokonać weryfikację modelu wybrane zostały współczynniki i hipotezy.
Na
początku została wyznaczona wariancja składnika resztowego
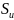 ,
wyznaczony został przy pomocy wzoru:
,
wyznaczony został przy pomocy wzoru:
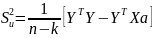
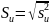
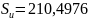
Kolejnym krokiem było określenie błędów średnich szacunku parametrów:
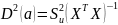
D(a1) = 0,0249,
D(a2) = 0,1152,
D(a3) = 428148,1011
Do wyznaczenia współczynnika zbieżności wykorzystany został wzór:
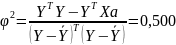
Współczynnik determinacji określony wzorem:
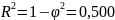
Ostatnim wyznaczonym współczynnikiem jest współczynnik zmienności losowej V:
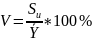
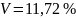
Zweryfikowany wzór modelu:
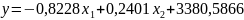
(0,0249) (0,1152) (428148,1011)
Statystyka t-Studenta
Statystyka t-Studenta została wykorzystana w celu sprawdzenia.
Hipoteza zerowa w postaci:
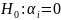
oraz hipotezę alternatywną w postaci:
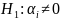
Dla statystyki testowej danej wzorem:
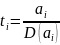
otrzymano następujące wartości:
t1 = -33,044
t2 = 2,08442
Dla poziomu istotności
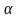 =0,1
oraz n=7 (liczba stopni swobody) z tablic testu t-Studenta
została odczytana wartość
=0,1
oraz n=7 (liczba stopni swobody) z tablic testu t-Studenta
została odczytana wartość
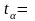 1,8946.
1,8946.
Dla poziomu istotności
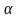 =0,1
dokonano następujących porównań:
=0,1
dokonano następujących porównań:
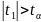 ,
bo 33,044 > 1,8946
,
bo 33,044 > 1,8946
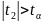 ,,
bo 2,08442 > 1,8946.
,,
bo 2,08442 > 1,8946.
Z wykonanych porównań wynika, że należy odrzucić hipotezę H0 i za słuszną uznać hipotezę alternatywną.
5. Statystyka F rozkładu Fischera Snedecora
Po wykonaniu sprawdzenia przy pomocy statystki t-Studenta wykonano sprawdzenia, czy dopasowanie oszacowanego modelu do danych empirycznych jest wystarczające. Wykorzystano w tym celu statystykę F rozkładu Fischera Snedecora. Na początku zostały określone hipotezy:
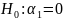 ʌ
ʌ
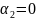 ʌ
ʌ
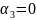
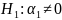 v
v
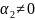 v
v
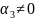
Korzystając ze statystyki określonej wzorem:
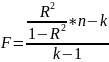
gdzie
R2=1-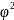 = 1-0,500 = 0,500
= 1-0,500 = 0,500
otrzymano
F = 8
Następnie z tablic Fischera Snedecora odczytano wartość krytyczną statystyki dla poziomu istotności α = 0,1 oraz stopni swobody m1=1 i m2=8 równą Fα = 3,46. Kolejnym krokiem było wykonanie porównania:
F>Fα , bo 8>3,46
Z wykonanego porównania wynika, że należy przyjąć hipotezę H1.
6. Graficzna prezentacja wyników
Dla otrzymanego wzoru określającego model ekonometryczny wykonano porównanie rzeczywistego przebiegu zmiennej objaśnianej z symulacyjnym przebiegiem tej zmiennej. Otrzymane wyniki przedstawiono w poniższej tabeli. Dodatkowo zaprezentowano wartość otrzymaną w kolejnym kroku (okresie) funkcji predykcyjnej dla danych z 2000 roku.
|
Rok |
Rzeczywisty Y |
Symulacyjny Y |
|
2003 |
786 |
959,4538 |
|
2004 |
1000 |
1110,029 |
|
2005 |
1450 |
1302,807 |
|
2006 |
1950 |
1696,591 |
|
2007 |
2270 |
2167,408 |
|
2008 |
2210 |
2438,132 |
|
2009 |
2100 |
2129,394 |
|
2010 |
2000 |
2088,224 |
|
2011 |
2060 |
2081,753 |
|
2012 |
2130 |
1982,413 |
|
2003 |
786 |
959,4538 |
Graficzne porównanie rzeczywistego Y z symulacyjnym:
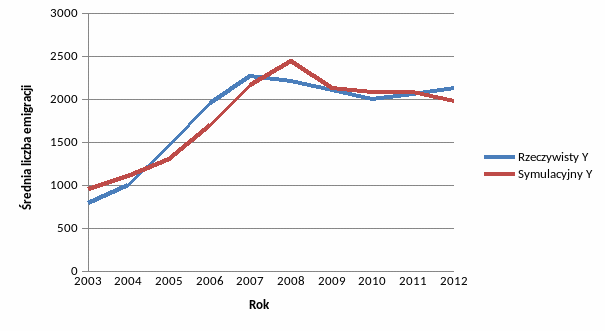
Wykres przedstawia średnią liczbę emigracji z Polski w latach 2003 – 2012. Wykres został sporządzony dokładnie z instrukcjami, które zostały podane na zajęciach.
7. Wnioski
Dzięki przeprowadzonym statystyką t-studenta i F rozkładu Fischera Snedecora, można stwierdzić, że zmienne objaśniające wpływają na zmienną endogeniczną. W oby przypadkach prawidłowe okazały się hipotezy H1 .
Dzięki graficznemu przedstawieniu modelu, również można potwierdzić poprawność sporządzonego modelu. Jak można zaobserwować przebiegi zmiennej objaśniającej i symulacyjnej są podobne. Oczywiście występują w nich drobne różnice, jednak wartości predykcyjne są bardzo bliskie realnym.
Opole 2015
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron