I zasada termodynamiki

W układzie zamkniętym zawierającym ciało proste zmiana energii wewnętrznej równa jest sumie algebraicznej pracy oraz ciepła wymienianego z otoczeniem, o ile nie występuje zmiana energii kinetycznej oraz energii położenia układu. Pierwsza zasada termodynamiki stwierdza możliwość zamiany ciepła na pracę.

Matematyczna forma zapisu I zasady termodynamiki ma postać:

dQ = dU + dL = dU + pdV [J] (7)

gdzie dU – różniczka zupełna, dQ i dL – różniczkowe wyrażenia liniowe

Ciepło dostarczane z zewnątrz do układu zamkniętego jest zużyte na przyrost jego energii wewnętrznej U oraz na wykonanie pracy zewnętrznej L.

Całkując równanie (7) otrzymuje się:

Q_1,2 = U₂ – U₁ + L_1,2 = U₂ – U₁ + 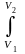p(V)dV (8)

Wprowadzono ekstensywną funkcję stanu zwaną entalpią oznaczoną przez I . Jest ona zdefiniowana następującym wzorem:

I = U + pV (9)

Entalpia jest sumą energii wewnętrznej układu i pracy zewnętrznej

Jeżeli w równaniu (2), wyrażającym pierwszą zasadę termodynamiki dla układu

zamkniętego, wstawimy w miejsce energii wewnętrznej entalpię, wówczas

praca zewnętrzna zamieni się na pracę techniczną i dla przemian odwracalnych

równanie to przyjmie postać:

Q_1,2 = I₂ – I₁ + L_t1,2 = I₂ – I₁ - 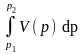(10)

czyli ciepło doprowadzone do czynnika powoduje przyrost entalpii oraz wykonanie pracy technicznej (rys. 2). Praca techniczna jest dodatnia przy rozprężaniu (dp<0) i ujemna przy sprężaniu (dp>0)

wzór na pracę techniczną L_t1,2 = 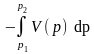(11)

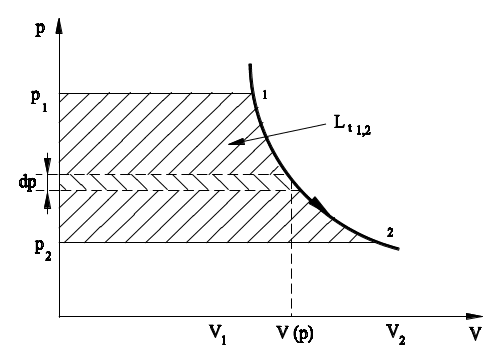
Rys. 2. Interpretacja graficzna pracy technicznej na wykresie p-V

Podczas przemiany przy stałym ciśnieniu i ogrzewaniu na podstawie równania (10) i (8) mamy:

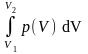Q_1,2 = I_1,2 – 0 = U_1,2 + (12)

Ponieważ Q_1,2 = Mc_p T_1,2 , gdzie c_p – ciepło właściwe przy stałym ciśnieniu,

M – masa układu, to równania (10) i (8) można zapisać następująco:

Q_1,2 = Mc_p T_1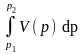,2 - = Mc_vT_1,2 + 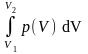(13)

Równanie (13) w postaci różniczkowej ma postać:

dQ = Mc_p dT – Vdp = Mc_v dT + p dV (14)

Po podzieleniu równania (14) przez T (przy T>0) i wykorzystaniu równania

stanu gazu doskonałego po odpowiednich przekształceniach przyjmie ono postać:

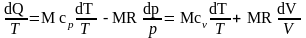(15)

Funkcja stojąca po lewej stronie równania została oznaczona przez dS

czyli:

dS = 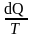(16)

i jest nazywana entropią układu [J/K]. Funkcja dS stanowi różniczkę zupełną

i jest ekstensywną funkcją stanu.