Przykład 15 - 14 -
Końce sztywnego pręta AB mogą ślizgać się po dwóch leżących w jednej płaszczyźnie prostych, przecinających się pod kątem β = 410. Należy wyznaczyć chwilową prędkość końca B pręta w położeniu określonym kątem α = 17.50 mierzonym tak jak na rys.15, jeśli wiadomo, że w rozpatrywanej chwili prędkość końca A równa jest VA = 3 m/s.
B
β
0 α A VA Rys.15
Rozwiązanie
B
VB cos(β-α)
VB
β-α
β
0 α A VA Rys.15.1
VAcosα
Z warunku że:
![]()
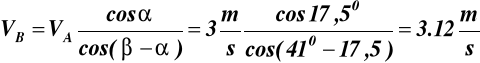
Przykład 16
Przedstawiony na rysunku 16 mechanizm składa się z trzech sztywnych prętów połączonych ze sobą przegubowo w punktach A i B. Pręt 01A obraca się wokół nieruchomego punktu 01, a pręt 02B wokół punktu 02, przy czym osie wszystkich punktów pozostają w jednej płaszczyźnie. Należy wyznaczyć prędkość punktu B w chwili, gdy pręty zajmują położenie jak na rysunku, jeżeli wiadomo, że prędkość końca A pręta 01A wynosi VA = 7 m/s.
Rozwiązanie - 15 -
VA αA = 0
A
900 300
600 αB B
VB
900
600 600
01 02 Rys.16
Z warunku że: ![]()
; ![]()
(16.1)
niewiadomy kąt αB określamy z warunku że suma kątów w czworoboku równa się 3600 czyli ![]()
![]()
![]()
; ![]()
Wstawiając αB do (16.1) 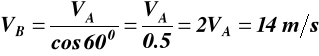
Przykład 17
Pręt AB o długości l = 3 m ślizga się końcem A po poziomej płaszczyźnie z prędkością VA = 3 m/s, koniec B zaś po płaszczyźnie tworzącej z poziomem kąt β = 410 (rys.17). Wyznaczyć prędkość punktu B dla t = 0,3 s.
Dane: dla t = 0, s = 0.
B
VB cos(β-α)
VB
β-α l
β
0 α A VA Rys.17
s
VAcosα
Rozwiązanie
![]()
stąd 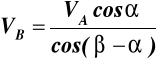
(17.1)
Aby określić VB musimy określić kąt α jako funkcję czasu t
Określenie s; 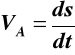
; ![]()
; ![]()
; ![]()
dla t = 0, s = 0 stąd C = 0 a wiec s =VA t
Określenie cos(β - α) - 16 -
z twierdzenia Snelliusa: 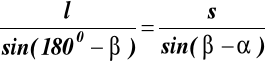
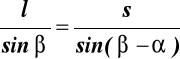
stąd 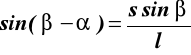
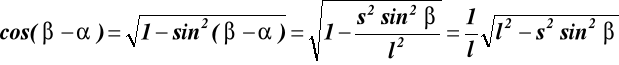
Określenie cosα
Z wzoru Carnota: ![]()
(17.2)
z twierdzenia Snelliusa: 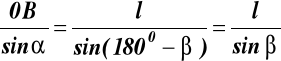
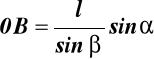
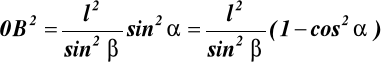
wstawiamy 0B2 do (17.2)
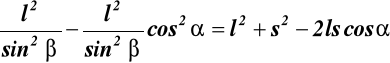
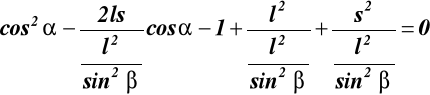
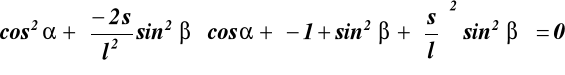
(17.3)
![]()
; oznaczmy: ![]()
;
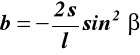
; 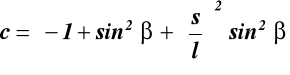
wstawiamy a, b i c do (17.3) otrzymujemy: ![]()
(17.4)
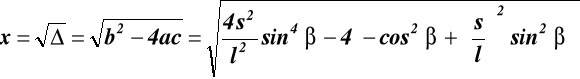
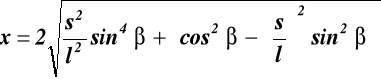
- 17 -
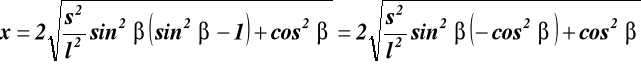
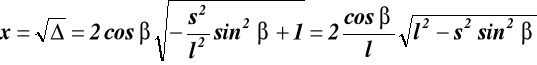
rozwiązanie równania (17.4)
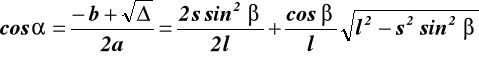
Wyznaczenie prędkości VB ze wzoru (17.1)
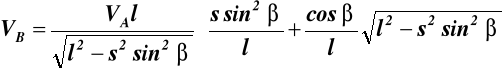
Odpowiedz:
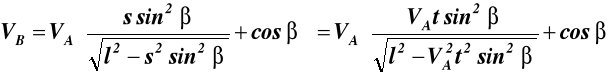
dla t = 0; s = 0; VB = VAcosβ =3 m/s cos410 = 2,26 m/s
dla ![]()
; ![]()
![]()
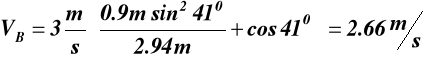
Przykład 18
Znając równanie ruchu postępowego prostoliniowego bryły A w postaci
s = 8 + 20t2 m (rys.18) wyznaczyć w ruchu obrotowym tarcz kołowych następujące prędkości i przyśpieszenia (kątowe i liniowe): ω1, ω2, VA, VM, VN, ε1, ε2, aA, aM, aN . Dane: r = 0.2 m, t = 2,3 s
M N
2r r r
s tarcza 1 tarcza 2
VA Rys.18
Rozwiązanie - 18 - Prędkość i przyspieszenie ciała A
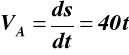
dla t = 2.3 s VA = 40·2.3 = 92 m/s s
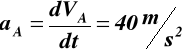
VA
Prędkość kątowa i przyśpieszenie kątowe tarczy 1, prędkość liniowa punktu M
![]()
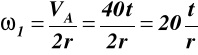
ω1 VM
dla t = 2.3 s 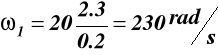
2r r
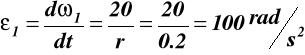
![]()
ε1 ![]()
VA
Prędkość kątowa i przyśpieszenie kątowe tarczy 2, prędkość liniowa punktu N
Prędkość liniowa punktu M i punktu N
są identyczne czyli VN = VM VM M VN N
stąd ![]()
a wiec ![]()
r ε2
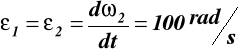
ω2
Przyspieszenia liniowe punktów M i N są takie same tarcza 2
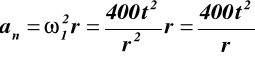
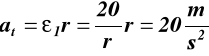
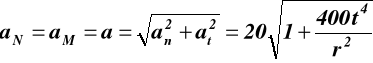
dla t = 2.3 s
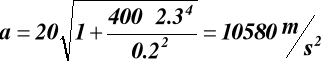
Wyszukiwarka