Ćwiczenie nr 8: „Wyznaczenie momentu bezwładności metodą dynamiczną.”.

Teoria:

Ciało sztywne obracające się wokół stałej osi definiują: punkt masowy m_i, prędkość kątowa ω, oraz prędkość liniowa, takie, że:

Całkowita energia kinetyczna ciała obracającego się dookoła osi przechodzącej przez środek masy:

Moment bezwładności: miara bezwładności ciała w ruchu obrotowym. Charakteryzuje rozkład masy w ciele. Moment bezwładności ciała względem osi z nazywane jest wyrażenie:

gdzie m_i - masy elementów ciała

Wzór na energię kinetyczną przyjmuje postać:

W ćwiczeniu będziemy posługiwać się krzyżakiem. Jest on osadzony na osi, wokół której może się obracać z minimalnymi oporami ruchu. Na osi krzyżaka nawinięty jest cienki sznurek z ciężarkiem masie m. Ciężarek ma wzg. Obranego poziomu odniesienia energię potencjalną:

Energia kinetyczna ruchu obrotowego wraz z energią kinetyczną ruchu postępowego tworzą:

Moment bezwładności krzyżaka otrzymamy poprzez podstawienie do powyższego wzoru:

,oraz

Wówczas:

Niepewność standardowa pomiaru:

, mierzone wielkości: t, r, h.

a więc:

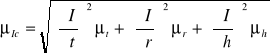
Obliczenia:

---