Wydział Inżynierii Elektrycznej i Komputerowej |
Koronowicz Łukasz |
Numer zespołu: 1 |
Ocena ostateczna |
Grupa 12 |
Badanie zależności oporu elektrycznego metali w zależności od temperatury. |
Numer ćwiczenia: 13 |
Data wykonania ćwiczenia: 02.03.2001 rok |
1. Wprowadzenie pojęć
Wahadło matematyczne - to punktowy ciężar zawieszony na nierozciągliwej, bezmasowej nici o długości l. W przypadku małych drgań wahadła matematycznego są one harmoniczne (w przybliżeniu, przy zaniedbaniu wyrazów proporcjonalnych do kwadratu i wyższych potęg sinusa kąta odchylenia). Jako model wahadła przyjmujemy ciężarek zawieszony na cienkim drucie lub lince, przy czym rozmiary ciężarka muszą być małe w stosunku do długości linki.
Ruch harmoniczny - (ruch drgający prosty) ruch, w którym współrzędne określające położenie punktu są opisane funkcjami trygonometrycznymi sinus lub cosinus, przyspieszenie jest proporcjonalne do wychylenia, przy czym współczynnik proporcjonalności jest ujemny.
![]()
Ruch harmoniczny opisany jest równaniem :
Gdzie A to amplituda, alfa to faza początkowa ruchu. Cały argument funkcji sinus to faza ruchu .
Okres ruchu harmonicznego T - jest to czas trwania jednego pełnego drgania, czyli czas powtarzania się jednego pełnego przemieszczenia albo cyklu.
Częstotliwość ruchu - jest to liczba drgań (albo cykli) na jednostkę czasu, częstotliwość to odwrotność okresu. Jej jednostką jest herc (Hz)
![]()
Prędkość ruchu harmonicznego:
Przyspieszenie ruchu harmonicznego:
![]()
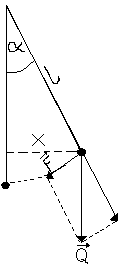
Wyprowadzenie wzoru na okres drgań wahadła matematycznego.
![]()
Z prostych zależności geometrycznych:
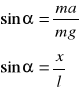
gdzie l oznacza długość wahadła.
A zatem
![]()
czyli ![]()
Gdy kąty wychylenia nici od położenia równowagi są małe, nie przekraczają 5-6 stopni można w przybliżeniu traktować odcinek x równy łukowi, czyli równy wychyleniu kulki od położenia równowagi.
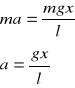
Wzór na przyspieszenie w naszym przypadku wygląda tak:
![]()
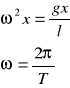
Przyrównujemy go z wcześniej uzyskanym równaniem:
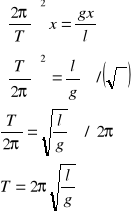
Więc:
![]()
Po przekształceniu uzyskujemy wzór:
Lp. |
l [cm] |
l [m] |
d [cm] |
d [m] |
10T [s] |
1T [s] |
1 |
86,3 |
0,863 |
1,9 |
0,019 |
18,6 |
1,86 |
2 |
86,5 |
0,865 |
1,9 |
0,019 |
18,4 |
1,84 |
3 |
86,2 |
0,862 |
1,9 |
0,019 |
18,7 |
1,87 |
4 |
86,3 |
0,863 |
|
|
18,7 |
1,87 |
5 |
|
|
|
|
18,2 |
1,82 |
6 |
|
|
|
|
19,0 |
1,90 |
7 |
|
|
|
|
18,9 |
1,89 |
8 |
|
|
|
|
18,4 |
1,84 |
9 |
|
|
|
|
18,6 |
1,86 |
10 |
|
|
|
|
18,3 |
1,83 |
|
86,3 |
0,863 |
1,9 |
0,019 |
18,6 |
1,86 |
Tabela Przeprowadzonych pomiarów:
l- długość nici
d- średnica kulki
10T - okres 10 wahnięć
T - okres jednego wahnięcia
3. Obliczenie niepewności pierwszego pomiaru
Obliczam niepewność korzystając z metody Studenta - Fishera.
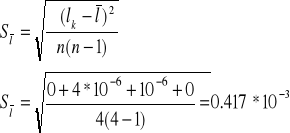
Obliczam odchylenie standardowe średniej:
Odczytuje z tablic współczynnik Studenta - Fishera i obliczam wynik:
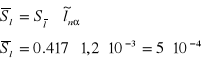
Więc otrzymuję wynik:
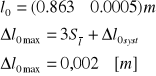
Obliczenie l całkowitego
W wyniku pomiarów otrzymałem średnicę ciężarka:
![]()
Całkowite l to :
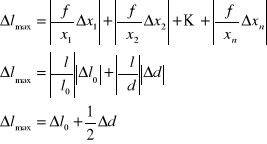
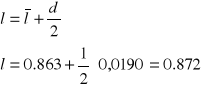
Obliczam błąd maksymalny przy pomocy wzoru na różniczkę zupełną:
Podstawiam uzyskane wartości:
![]()
Uzyskałem wynik:
![]()
3 .Obliczenie niepewności trzeciego pomiaru
Obliczam średni czas
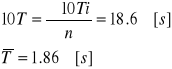
Obliczam odchylenie standardowe:
![]()
Obliczam błąd maksymalny
![]()
Otrzymałem wynik:
![]()
3d. Obliczenie wyniku końcowego
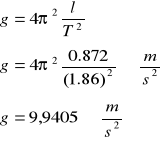
Korzystam z przekształconego wzoru na okres drgań wahadła matematycznego i obliczam g:
Obliczam błąd względny :
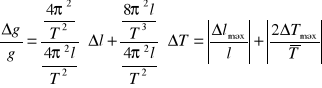
Obliczam błąd maksymalny:
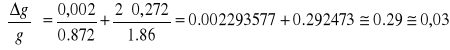
Otrzymałem wynik końcowy:
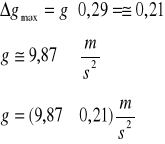
![]()
![]()
![]()
![]()
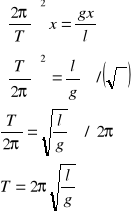
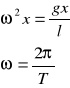
![]()
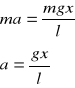
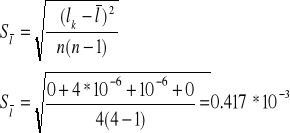
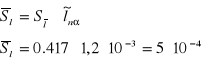
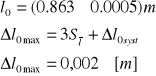
![]()
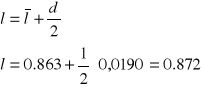
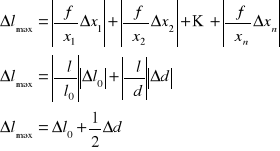
![]()
![]()
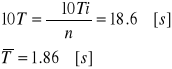
![]()
![]()
![]()
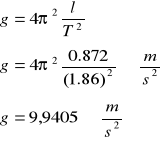
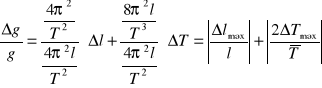
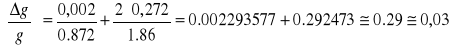
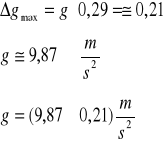
Wyszukiwarka