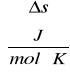stąd:

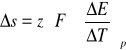
Znając
oraz
można obliczyć
na podstawie równania:

Równanie Nersta na SEM badanego ogniwa:

gdzie:

-potencjał normalny

-stężenie jonów metalu w roztworze

OPRACOWANIE WYNIKÓW:

TABELA POMIAROWA

Temperatura [°C]	SEM
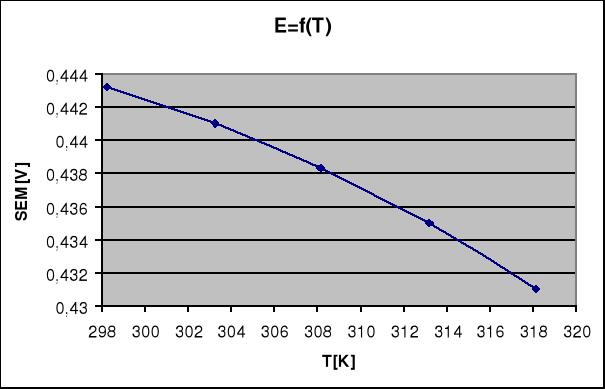
25,1	0,44324	-85532,3	-	-
30,1	0,44102	-85103,9	85,7	-82524,3
35	0,43832	-84582,6	106,3	-80862,1
40,05	0,43502	-83946,1	126,1	-78895,8
45	0,43102	-83174,2	155,9	-76158,7

Sposób obliczeń:

OPRACOWANIE WYNIKÓW

Dla temperatur 25.2 30.2 35.2 40.2 45.2 ⁰C wyznaczamy
.

1. Obliczamy entalpię swobodną :

= z * F * E

z = 2

F = 96485,31 [C/mol]

- dla 25,1 ⁰C E = 0,44324 [V]

= - 2 * 96485,31 * 0,44324 = -85532,3

- dla 30,1 ⁰C E = 0,44102 [V]

= -85103,9

- dla 35 ⁰C E = 0,43832 [V]

= -84582,6

- dla 40,05 ⁰C E = 0,43502 [V]

= -83946,1

- dla 45 ⁰C E = 0,43102 [V]

= -83174,2

2. Obliczam entropię :

= z * F *

z = 2

F = 96485,31 [C/mol]

• dla 25,1 ⁰C

= 0

• dla 30,1 ⁰C ΔT = 5K ΔE=2,22*10^-3

= 85,7 [J/mol *K]

• dla 35 ⁰C ΔT =4,9K ΔE=2,7*10^-3

= 106,3[J/mol * K]

• dla 40,05 ⁰C ΔT = 5,05K ΔE=3,3*10^-3

= 126,1 [J/mol * K]

• dla 45 ⁰C ΔT = 4,95K ΔE=4*10^-3

=155,9 [J/mol * K]

3. Obliczamy zależność SEM od temperatury :

z = 2

F = 96485,31

- dla T=25,1 ⁰C
= 0

= 0

- dla T=30,1 ⁰C
= 85,7

= 4,4*

- dla T=35 ⁰C
=106,3

= 5,5 *

- dla T=40,05 ⁰C
= 126,1

= 6,5 *

- dla T=45 ⁰C
= 155,5

= 8,1 *

4. Obliczamy entalpię :

T = 25,1 ⁰C

0

T = 30,1 ⁰C

-82524,33

T = 35 ⁰C

-80862,1

T = 40,05 ⁰C

-78895,8

T = 45 ⁰C

-76158,7

Wykres zależności E=f(T):

---