Nr ćwiczenia: 25	Temat ćwiczenia: Wyznaczanie stosunku Cp/Cv dla powietrza i dwutlenku węgla metodą akustyczną	Ocena z teorii:
Numer grupy: 7	Mariusz Cedzidło	Ocena ze sprawozdania:
Data wykonania: 19.03.1997	Wydział Elektrotechniki, Automatyki i Elektroniki	Automatyka i Robotyka Rok I Grupa 1

Wprowadzenie teoretyczne.

Fale dźwiękowe powstają w wyniku drgań układów drgających np.membrana, struna. Fale takie mogą być poprzeczne i podłużne w zależności od kierunku drgań i kierunku rozchodzenia się zaburzenia. W cieczach i gazach rozchodzić się mogą wyłącznie drgania podłużne. Za fale dźwiękowe przyjmowane są fale słyszalne przez ucho ludzkie, tzn. z przedziału częstotliwości 20-20000 Hz. W przestrzeni może przebiegać kilka niezależnych od siebie fal i przemieszczenie cząstki w ustalonej chwili jest wypadkową (sumą) przemieszczeń pochodzących od poszczególnych zaburzeń. Jeśli fale pochodzą od koherentnych źródeł, to mogą ze sobą interferować. W wyniku nałożenia dwóch fal biegnących przeciwnie do siebie powstanie fala stojąca. Jeżeli układ wykonujący drgania jest pobudzany periodyczną serią impulsów, to może zostać wprawiony w drgania o dużej amplitudzie. Zjawisko to nazywa się rezonansem.

Zasada ekwipartycji energii.

Obliczamy całkowitą energię układu cząstek dla gazu doskonałego. Na energię cząstki składają się:

- energia kinetyczna jej ruchu postępowego i obrotowego,

- energia potencjalna drgania atomu.

W przypadku dużej ilości cząstek ich aproksymowana średnia wartość jest taka sama, zależna jedynie od temperatury. Zgodnie z zasadą ekwipartycji energii dla każdego stopnia swobody gazu przypada energia kinetyczna kT/2. Widać stąd, że nie zależy ona od ciśnienia, objętości a jedynie od temperatury. Jest to cenne źródło informacji o cieple właściwym gazu doskonałego.

Rozróżniamy odpowiednie ciepła właściwe dla gazów:

C_p - przy stałym ciśnieniu,

C_v - przy stałej objętości.

Ogólne różniczkowe równanie fali jest postaci:

gdzie: k₀ - parametr ściśliwości, r₀ - gęstość.

Rozwiązaniem tego równania jest funkcja zależna od położenia i czasu.

x(x,t)= x(x-vt)

c₀ możemy zastąpić adiabatycznym modułem sprężystości c=C_p/C_v.

Korzystając z równania Clapeyron'a pV/T = nR otrzymujemy :

v²=RTc/m

c zależy bezpośrednio od liczby stopni swobody:

C_v=RnT/2 => c=(n+2)/n

Doświadczalnie wyznaczone wartości c dla temperatury pokojowej różnią się od wartości teoretycznych i są zależne od temperatury. Jest to wynikiem faktu, że prawo ekwipartycji energii jest słuszne w przypadku gdy odległości poziomów energetycznych odpowiadających sobie rotacjom i oscylacjom jest mniejsze od kT.

	gazy jednoatomowe	gazy dwuatomowe	gazy wieloatomowe
Ek / cząstkę	3/2 kT	5/2 kT	3 kT
Cv	3/2 RT	5/2 RT	3 RT
Cp	5/2 RT	7/2 RT	4 RT
c	5/3	7/5	4/3

W gazie istnieją różnice w prędkościach poszczególnych cząstek. Każdy gaz posiada swój charakterystyczny rozkład prędkości cząstek od temperatury. Możemy jednak na podstawie prawa Maxwella znaleźć najbardziej prawdopodobny rozkład prędkości, przy czym dla małych prędkości zachodzi niewielki rozrzut w ich wartościach.

Przeciętną prędkością cząstek jest pierwiastek z v² zwany również średnią prędkością kwadratową.

3.Przebieg ćwiczenia.

Ćwiczenie przeprowadzamy w oparciu o aparaturę zawierającą urządzenie zwane rurą Quincke'go. Generator akustyczny wraz z głośnikiem wytwarza falę dźwiękową o wcześniej ustalonej częstotliwości. Regulując wysokość słupa wody w rurze Quincke'go dążymy do uzyskania fali stojącej. W tym przypadku uzyskamy maksymalne wzmocnienie dla odległości głośnik-słup wody równej całkowitej wielokrotności połowy długości fali ( l/2)n.

Tabela pomiarowa.

a) dla powietrza

v=lf.

1/f [s]	f [Hz]	l [m]	v [m/s]	Dv [m/s]
0.0025	400	0.838	335.2	1.00
0.0018	560	0.6	336	1.80
0.0013	800	0.416	332.4	-1.8
0.0010	1040	0.308	320.3	-
0.0007	1500	0.222	333	-1.2

Średnia prędkość v wynosi 334.2 [m/s] z odchyleniem standartowym 1.7[m/s].

b) dla dwutlenku węgla.

1/f [s]	f [Hz]	l [m]	v [m/s]
0.0017	600	0.434	260.1

Prędkość v w dwutlenku węgla wynosi 260.1 [m/s] z dokładnością 0.1.

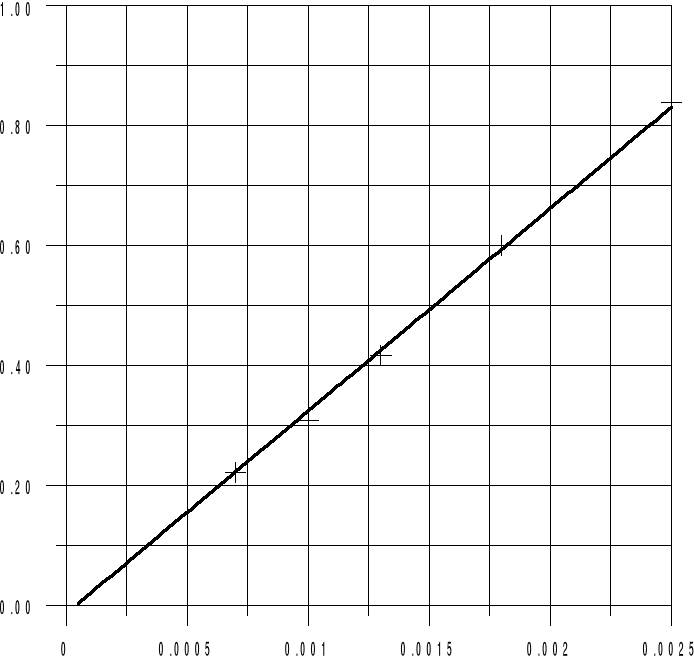
Zależność l=f(1/f)

Obliczanie współczynników prostej na podstawie metody najmniejszych kwadratów.

a=1.335 ; b= -0.007.

Wyznaczanie k=C_p/C_v oraz i.

gdzie: M - masa cząsteczkowa, R- stała gazowa, v- prędkość dźwięku, T- temperatura gazu w K, i- liczba stopni swobody molekuły, C_p,C_v - ciepła właściwe.

M = 0.044 [kg/mol] (CO₂); v=334.2 [m/s] ( powietrze), 260.1 [m/s] (CO₂); R= 8.3143JK^-1mol^-1 ; T=291[K]. Aby obliczyć masę molową powietrza przyjmujemy jego skład jako: 78%N₂ , 21%O₂ 1%Ar (jest go najwięcej spośród innych gazów) . Tak określona masa molowa powietrza równa jest 0.028 [kg/mol].

k_powietrza = 1.29 [/]

k_CO = 1.23 [/].

Liczba stopni swobody:

- dla powietrza i=7,

- dla CO₂ i= 9.

Obliczanie średniej prędkości kwadratowej.

Jest ona równa:

a) dla powietrza v_śr.kw.=551.9 [m/s]

b) dla CO₂ v_śr.kw.=396.7 [m/s].

Wnioski:

1. Pomiar maksimów interferencyjnych obarczony jest błędem ze względu na subiektywny odbiór rejestrującego. Niedokładność pomiaru wzrasta ze zwiększeniem częstotliwości fali akustycznej.

2. Prędkość rozchodzenia się fali zależy od ośrodka, w którym propaguje oraz temperatury tego ośrodka.

3. W związku z tym, że powietrze znajdujące się w rurze Quincke'go zawierało cząsteczki parującej wody, mogliśmy błędnie wyznaczyć k, a co za tym idzie liczbę stopni swobody.

4. Błąd bezwzględny stosunku C_p/C_v wynosi: 4 10^-5

%

---