Dyfrakcja elektronów na polikrystalicznej warstwie grafitu.

1. Cel ćwiczenia

Celem ćwiczenia jest obserwacja zjawiska dyfrakcji elektronów oraz pomiar odległości międzypłaszczyznowych w graficie.

2. Przebieg pomiaru

Wszystkie fale, niezależnie od rodzaju ulegają odbiciu, załamaniu, dyfrakcji i interferencji. Procesy te są wynikiem wzajemnego oddziaływania fali i cząstek ośrodków, które fala napotyka na swojej drodze. Badanie powyższych zjawisk jest szeroko wykorzystywane do określania struktury ośrodka. Celem ćwiczenia było wyznaczenie odległości międzypłaszczyznowych w polikrystalicznej warstwie grafitu oraz obserwacja zjawiska dyfrakcji elektronów.

W szklanej lampie próżniowej znajdują się :

1. K - katoda (źródło elektronów)

2. H - cylinder Wehnelta (regulacja natężenia wiązki elektronów)

3. G - elektrody ogniskujące wiązkę

4. A - anoda

5. P - grafit polikrystaliczny

6. E - ekran pokryty luminoforem

3. Opracowanie pomiarów

Tabela wartości napięć anodowych U_A i odpowiadających im średnic D

dla każdego z pierścieni.

Pomiar 1:

Lp.	Napięcie anodowe [V]	Mniejszy okrąg [mm]	Większy okrąg [mm]
1.	4000	27	48
2.	4500	25	44
3.	5000	23	42
4.	5500	22	38
5.	6000	21	37
6.	6500	20	34
7.	7000	19	32
8.	7500	18	31
9.	8000	18	31
10.	8500	18	30
11.	9000	17	29

Pomiar 2:

Lp.	Napięcie anodowe [V]	Mniejszy okrąg [mm]	Większy okrąg [mm]
1.	4000	28	46
2.	4500	27	44
3.	5000	24	40
4.	5500	23	37
5.	6000	22	36
6.	6500	21	34
7.	7000	20	32
8.	7500	20	32
9.	8000	18	31
10.	8500	17	30
11.	9000	17	29

Pomiar 3:

Lp.	Napięcie anodowe [V]	Mniejszy okrąg [mm]	Większy okrąg [mm]
1.	4000	27	47
2.	4500	26	44
3.	5000	24	41
4.	5500	22	37
5.	6000	21	36
6.	6500	20	34
7.	7000	20	32
8.	7500	19	31
9.	8000	18	31
10.	8500	17	30
11.	9000	16	29

4. Obliczenie wartości sin

W celu wyznaczenia wartości sin
musimy znaleźć sin4
, a następnie kąt
.

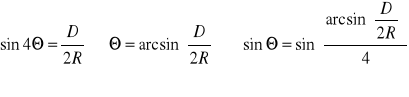
gdzie:

D - średnica okręgów

R = 65mm - promień lampy

Wyznaczone wartości
dla mniejszego i większego okręgu

Pomiar 1:

Lp.		Mniejszy okrąg [mm]		[rad]		Większy okrąg [mm]		[rad]
1	0,015811388	27	0,207692307	11,9871497	0,05227966	48	0,369230769	21,6681846	0,0944045
2	0,014907119	25	0,192307692	11,0874891	0,04835943	44	0,338461538	19,7831703	0,08621321
3	0,014142135	23	0,176923076	10,1905887	0,04445018	42	0,323076923	18,8491065	0,08215205
4	0,013483997	22	0,169230769	9,7430973	0,04249948	38	0,292307692	16,9961647	0,0740918
5	0,012909944	21	0,161538461	9,2962052	0,04055123	37	0,284615384	16,5358596	0,07208871
6	0,012403473	20	0,153846153	8,849883	0,0386053	34	0,261538461	15,1613685	0,06610571
7	0,011952286	19	0,146153846	8,4041015	0,03666159	32	0,246153846	14,2500326	0,06213744
8	0,011547005	18	0,138461538	7,9588318	0,03471998	31	0,238461538	13,7957568	0,060159
9	0,011180339	18	0,138461538	7,9588318	0,03471998	31	0,238461538	13,7957568	0,060159
10	0,010846522	18	0,138461538	7,9588318	0,03471998	30	0,23076923	13,3423637	0,05818416
11	0,010540925	17	0,130769230	7,5140454	0,03278033	29	0,223076923	12,88982	0,0562128

Pomiar 2:

Lp.		Mniejszy okrąg [mm]		[rad]		Większy okrąg [mm]		[rad]
1	0,015811388	28	0,215384615	12,4380927	0,05424478	46	0,353846153	20,7227443	0,09029687
2	0,014907119	27	0,207692307	11,9871497	0,05227966	44	0,338461538	19,7831703	0,08621321
3	0,014142135	24	0,184615384	10,6387092	0,04640346	40	0,307692307	17,920213	0,07811203
4	0,013483997	23	0,176923076	10,1905887	0,04445018	37	0,284615384	16,5358596	0,07208871
5	0,012909944	22	0,169230769	9,7430973	0,04249948	36	0,276923076	16,0766497	0,0700901
6	0,012403473	21	0,161538461	9,2962052	0,04055123	34	0,261538461	15,1613685	0,06610571
7	0,011952286	20	0,153846153	8,849883	0,0386053	32	0,246153846	14,2500326	0,06213744
8	0,011547005	20	0,153846153	8,849883	0,0386053	32	0,246153846	14,2500326	0,06213744
9	0,011180339	18	0,138461538	7,9588318	0,03471998	31	0,238461538	13,7957568	0,060159
10	0,010846522	17	0,130769230	7,5140454	0,03278033	30	0,230769230	13,3423637	0,05818416
11	0,010540925	17	0,130769230	7,5140454	0,03278033	29	0,223076923	12,88982	0,0562128

Pomiar 3:

Lp.		Mniejszy okrąg [mm]		[rad]		Większy okrąg [mm]		[rad]
1	0,015811388	27	0,207692307	11,9871497	0,05227966	47	0,361538461	21,1947082	0,0923476
2	0,014907119	26	0,2	11,5369590	0,05031822	44	0,338461538	19,7831703	0,08621321
3	0,014142135	24	0,184615384	10,6387092	0,04640346	41	0,315384615	18,3840342	0,08012948
4	0,013483997	22	0,169230769	9,7430973	0,04249948	37	0,284615384	16,5358596	0,07208871
5	0,012909944	21	0,161538461	9,2962052	0,04055123	36	0,276923076	16,0766497	0,0700901
6	0,012403473	20	0,153846153	8,8498830	0,0386053	34	0,261538461	15,1613685	0,06610571
7	0,011952286	20	0,153846153	8,8498830	0,0386053	32	0,246153846	14,2500326	0,06213744
8	0,011547005	19	0,146153846	8,4041015	0,03666159	31	0,238461538	13,7957568	0,060159
9	0,011180339	18	0,138461538	7,9588318	0,03471998	31	0,238461538	13,7957568	0,060159
10	0,010846522	17	0,130769230	7,5140454	0,03278033	30	0,230769230	13,3423637	0,05818416
11	0,010540925	16	0,123076923	7,0697140	0,03084255	29	0,223076923	12,88982	0,0562128

5. Wykresy prostych
oraz obliczenie współczynników nachylenia prostych metodą najmniejszych kwadratów.

Pomiar 1:

1. mniejszy okrąg:

współczynnik nachylenia prostej a₁= 3,624302 1/v

błąd współczynnika nachylenia Δa₁= 0,150995 1/v

współczynnik korelacji r = 0,99228

2. większy okrąg

współczynnik nachylenia prostej a₂= 7,342855 1/v

błąd współczynnika nachylenia Δa₂= 0,320083 1/v

współczynnik korelacji r = 0,99156

Pomiar 2:

1. mały okrąg

współczynnik nachylenia prostej a₁= 4,182607 1/v

błąd współczynnika nachylenia Δa₁= 0,181276 1/v

współczynnik korelacji r = 0,99165

2. duży okrąg

współczynnik nachylenia prostej a₂= 6,572648 1/v

błąd współczynnika nachylenia Δa₂= 0,288804 1/v

współczynnik korelacji r = 0,99142

Pomiar 3:

1. mały okrąg

współczynnik nachylenia prostej a₁= 4,002356 1/v

błąd współczynnika nachylenia Δa₁= 0,158632 1/v

współczynnik korelacji r = 0,993

2. duży okrąg

współczynnik nachylenia prostej a₂= 6,96244 1/v

błąd współczynnika nachylenia Δa₂= 0,322315 1/v

współczynnik korelacji r = 0,99049

6. Obliczenie odległości międzypłaszczyznowych d

gdzie:

- stała Plancka,

a - współczynnik nachylenia prostej,

- masa spoczynkowa elektronu,

- ładunek elektronu

Pomiar 1:

Pomiar 2:

Pomiar 3:

7. Obliczenie błędu wielkości d metodą różniczki zupełnej

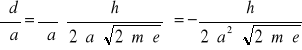
Pomiar 1:

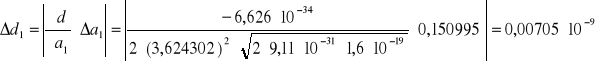
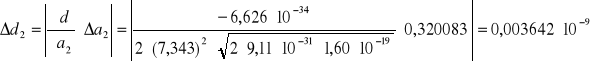
Pomiar 2:

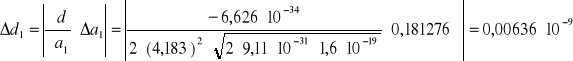
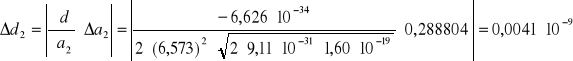
Pomiar 3:

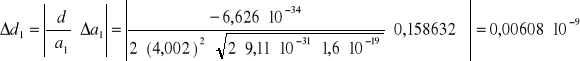
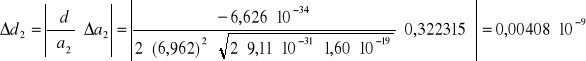
8. Błędy względne

Pomiar 1:

Pomiar 2:

Pomiar 3:

9. Wnioski

Błędy w pomiarach mogą być spowodowane niedokładnością w odczytywaniu wyników przez osoby wykonujące ćwiczenie lub z niedokładności sprzętu pomiarowego. Jednakże biorąc pod uwagę wartość korelacji wydaje mi się, że pomiary wykonane są z dużą dokładnością.

12

---