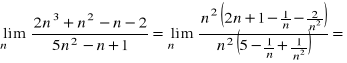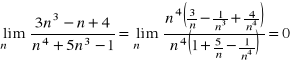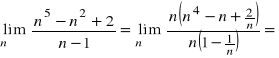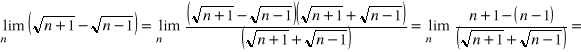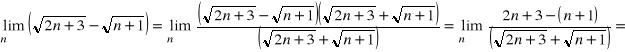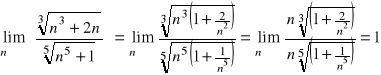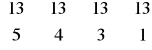Odpowiedź do zadania 1:
1 m - a zł.
2 m - a + b zł.
3 m - (a + b) + b zł.
a1 = a; r = b
an = a1 + (n - 1)⋅r = a + 39b
Sn = ![]()
.
Koszt budowy studni o głębokości 40 metrów wyniesie 40a + 780b.
Powrót
Odpowiedź do zadania 2:
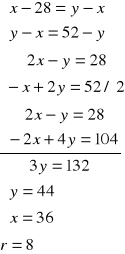
Szukany ciąg to: 28, 36, 44, 52.
Powrót
Dowód prawdziwości wzoru na sumę ciągu geometrycznego: 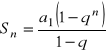
(gdy q ≠ 1)
Dowód:
Krok 1: n = 1
L = a1; P = 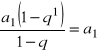
; L = P ok.
Krok 2: Założenie indukcyjne: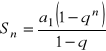
Teza indukcyjna: 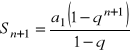
(w miejsce n podstawiamy n + 1)
Dowód indukcyjny:
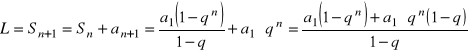
=
z założenia
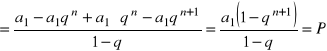
ok.
Powrót
Odpowiedź do zadania 3:
Ponieważ podków jest 4, a hufnali w podkowie po 6, wystarczy policzyć sumę 24-wyrazowego ciągu geometrycznego o q = 2:
1 + 2 + 22 + 23 + … +223 = ![]()
połuszek =
41943 ruble i 3,75 kopiejki
Jak widać, już w roku 1703 trzeba było uważać na niezwykle korzystne oferty. No a przede wszystkim należy pamiętać, że ciąg geometryczny o q > 1 rośnie bardzo szybko.
Powrót
Odpowiedź do zadania 4:
Nasze trzy liczby to: ![]()
Ich iloczyn jest równy 13824, czyli
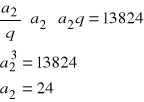
Ich suma jest równa 126, czyli
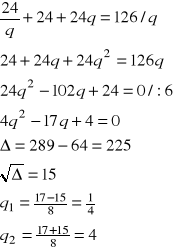
Szukane ciągi to: 6, 24, 96 lub 96, 24, 6.
Powrót
Odpowiedź do zadania 5:
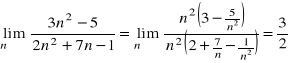
,
ponieważ ![]()
Metoda polega na wyciągnięciu przed nawias w liczniku i w mianowniku n w najwyższej potędze mianownika.
ponieważ ![]()
Uwaga: Ciąg, którego granica wynosi nieskończoność nazywamy ciągiem rozbieżnym.
ponieważ ![]()
ponieważ ![]()
![]()
, bo mianownik dąży do nieskończoności.
Metoda polega na przemnożeniu licznika i mianownika przez sumę tych pierwiastków. Chodzi o to, by móc skorzystać ze wzoru ![]()
.
Możemy tu oczywiście wyciągnąć przed nawias najwyższą potęgę mianownika, czyli pierwiastek z n. Ale możemy też przeprowadzić następujące rozumowanie: stopień licznika jest 1, stopień mianownika jest ![]()
, zatem stopień licznika jest większy niż stopień mianownika, a więc w granicy wyjdzie nieskończoność. (Gdyby stopień licznika był mniejszy od stopnia mianownika wyszłoby 0.)
Dlaczego? Ponieważ ![]()
, a ![]()
.
Powrót
Odpowiedź do zadania 6:
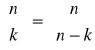
k = 5
n - k = 9
n - 5 = 9
n = 14
Powrót
Odpowiedź do zadania 7:
Rozwiązanie: 9 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 = 1080.
Uzasadnienie: Wszystkie liczby od 0 do 9 są podzielne przez 1, ale zero nie może wystąpić na pierwszej pozycji, bo wówczas liczba nie będzie pięciocyfrowa. Do wyboru pozostaje 9 liczb. Wśród liczb od 0 do 9 pięć jest podzielnych przez 2, cztery przez 3, trzy przez 4 i dwie przez 5. Z twierdzenia o mnożeniu uzyskujemy oczekiwany wynik.
Powrót
Odpowiedź do zadania 8:
Rozwiązanie:
6 ⋅ 2 = 12
Na kostce mamy 6 oczek, więc 6 możliwości, zaś na moneta ma dwie strony (orzeł, reszka), więc mamy 2 możliwości. Z twierdzenia o mnożeniu, mnożymy 6 ⋅ 2.
6 ⋅ 2 ⋅ 52 ⋅ 51 = 31 824
Na kostce mamy 6 oczek, więc 6 możliwości, zaś na moneta ma dwie strony (orzeł, reszka), więc mamy 2 możliwości. Poza tym losujemy dwie dowolne karty z 52, czyli ciągnąc pierwszą kartę mamy 52 możliwości, a ciągnąc drugą kartę mamy 51 możliwości, bo w talii kart nie ma już tej pierwszej wylosowanej karty. Z twierdzenia o mnożeniu, mnożymy 6 ⋅ 2 ⋅ 52 ⋅ 51.
Powrót
Odpowiedź do zadania 9:
Rozwiązanie:
9 ⋅ 103 = 9000
Aby liczba była czterocyfrowa, pierwsza cyfra nie może być zerem. Wybieramy ją spośród liczb od 1 do 9, czyli na 9 sposobów. Pozostałe trzy cyfry mogą być dowolne i mogą się powtarzać, więc każdą można wybrać na 10 sposobów. W sumie daje to 103.9 ⋅ 9 ⋅ 8 ⋅ 7
Aby liczba była czterocyfrowa, pierwsza cyfra nie może być zerem. Wybieramy ją spośród liczb od 1 do 9, czyli na 9 sposobów. Po tym wyborze w puli pozostaje jeszcze 9 cyfr. Z nich możemy wybierać drugą cyfrę na 9 sposobów. Trzecią możemy wybrać już tylko na 8 sposobów, a czwartą na 7 sposobów.
Powrót
Odpowiedź do zadania 10:
Rozwiązanie: Liczba 180 po rozpisaniu na czynniki pierwsze ma postać:
180 = 22 ⋅ 32 ⋅ 51
Każdy dzielnik tej liczby ma postać:
d = 2k ⋅ 3m ⋅ 5n
gdzie k ∈ {0, 1, 2}, m ∈ {0, 1, 2}, n ∈ {0, 1}
Wykładnik k możemy wybrać na trzy sposoby, m też na trzy, a n na dwa sposoby. Zatem liczba dzielników 180 to: 3 ⋅ 3 ⋅ 2 = 18.
Powrót
Odpowiedź do zadania 11:
7! = 5040
Skoro szyfr jest złożony z 7 cyfr i nie mamy żadnych dodatkowych założeń, trzeba będzie wykonać 7! prób. Są to po prostu wszystkie permutacje 7-elementowego zbioru.
4! ⋅ 3! = 24 ⋅ 6 = 144
Ponieważ naszemu biznesmenowi przypomniało się, że wszystkie trzy ostatnie cyfry są ze zbioru {5,6,7} to na trzech ostatnich miejscach mamy 3! Możliwości ustawienia 3 cyfr, a na czterech pierwszych miejscach 4!, ponieważ są to permutacje pozostałych liczb, czyli {1,2,3,4}.
Powrót
Odpowiedź do zadania 12:
n!
Zwykłe permutacje osób, czyli n! możliwości.
Dlaczego przy okrągłym stole mamy tych możliwości mniej i to n razy? Oczywiście tak jest tylko wtedy, gdy chcemy za dwa różne ustawienia uważać te, że przynajmniej jedna osoba ma innego sąsiada z prawej lub z lewej strony. Jeśli bowiem chcielibyśmy zwracać uwagę również na usytuowanie względem otoczenia, to nadal będzie n! Chodzi po prostu o to, że w przypadku okrągłego stołu część ustawień osób, które w rzędzie były różne, tu będą obrotami ze względu na „sklejenie” końców. Aby to dobrze zrozumieć najlepiej wykonać ćwiczenie praktyczne, czyli poprzestawiać np. pięć osób w rzędzie, a następnie w kole.
Powrót
Odpowiedź do zadania 13:
Z 12 dobrych żarówek wybieramy 5. Możemy to zrobić na ![]()
sposobów.
Powrót
Odpowiedź do zadania 14:
Spośród 13 pików wybieramy 5 kart, z 13 kierów 4 karty, z 13 kar 3 karty i z 13 trefli jedną. I oczywiście wszystko mnożymy z twierdzenia o mnożeniu.
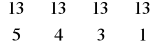
⋅ 4!
Wybieramy karty tak, jak poprzednio, ale układ kolorów może być dowolny. Dlatego mamy 4! razy możliwości więcej, bo tyle jest permutacji 4 kolorów.
Powrót
Odpowiedź do zadania 15:
35 = 243
Można utworzyć właśnie tyle liczb ponieważ są to wariacje z powtórzeniami. Na każdym miejscu można postawić jedną z trzech cyfr. Czyli na pierwszym miejscu jest 3 możliwości, na drugim trzy, na trzecim trzy, na czwartym trzy i na piątym też trzy.
Powrót
Odpowiedź do zadania 16:
![]()
Można utworzyć właśnie tyle liczb ponieważ są to wariacje bez powtórzeń. Mamy 9 cyfr i tworzymy z nich liczbę 5-cyfrową tak, aby żadna cyfra się nie powtórzyła.
Powrót
Rozwiązanie zagadki 1:
W tej grupie studenckiej były bliźnięta.
Powrót
Wyszukiwarka