Zadanie nr 20

Zaproponować postać analityczną modelu tendencji rozwojowej przedstawiające kształtowanie się wielkości obrotów w pewnej spółce handlowej (y_t w tys. zł) z latach

1968 - 1997, mając dane zawarte w poniższej tablicy:

Lata	yt	Lata	yt
1968	8	1983	40
1969	5	1984	38
1970	15	1985	45
1971	13	1986	51
1972	16	1987	47
1973	18	1988	60
1974	17	1989	64
1975	21	1990	61
1976	19	1991	63
1977	23	1992	72
1978	25	1993	75
1979	20	1994	79
1980	24	1995	76
1981	27	1996	90
1982	22	1997	92

Za cel postawiliśmy sobie osiągnięcie modelu, który będzie w jak najlepszym stopniu odwzorowywał rzeczywistość (jak najwyższe R² oraz jak najniższe V). W jego szacowaniu posłużymy się metodą najmniejszych kwadratów. Obliczenia zostaną wykonane za pomocą programu Excel tu zostaną zademonstrowane ostateczne wyniki. Przy weryfikacji hipotez istotności zakładamy współczynnik α=0,05.

Rozwiązanie

Poniżej graficzna prezentacja danych do zadania

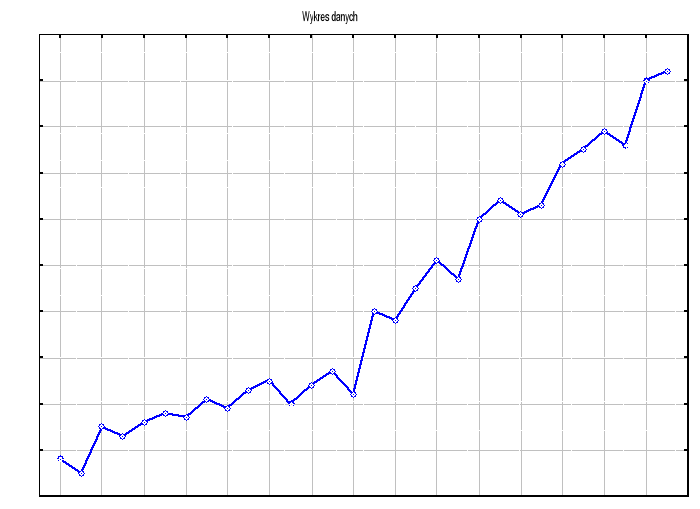
Do zbadania zależności danych oraz w celu zaproponowania modelu analitycznego modelu, przeprowadzimy analizę danych po przez :

1. funkcję
   ,

2. funkcję
   ,

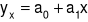
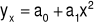
3. funkcję
   .

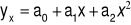
Ad.1

Parametry funkcji liniowej, przedstawionej poniżej :

będziemy szacować za pomocą MNK. Wektor parametrów rozwiązania obliczamy wg wzoru:

za macierz X podstawiamy kolejne liczby, będące numerami kolejnych obserwacji tj. dla roku 1967 - 1 , dla 1997 roku - 30, otrzymując ( patrz poniżej) macierz X. Macierz Y otrzymujemy przez przypisanie do niej wyników obserwacji.

Kolejnym krokiem jest transpozycja macierzy X :

Macierz X^T mnożymy przez macierz X otrzymując macierz o wymiarach 2 x 2

Aby otrzymać macierz odwrotną, badamy czy macierz ta, nie jest macierzą osobliwą, tzn

det (X) = 0

Obliczamy wyznacznik macierzy, który dla tego przypadku wynosi: 67425 tzn.
. Macierz odwrotna istnieje, więc przedstawiamy ją poniżej:

Następnym krokiem jest obliczenie ilorazu X^TY, który jest wektorem kolumnowym i wynosi:

Ostatnim krokiem w celu obliczenia wektora rozwiązań równania jest obliczenie iloczynu macierzy (X^TX)^-1(X^TY)

Powyższa macierz jest macierzą parametrów naszego równania. Możemy przypisać odpowiednio

oraz

Uzyskujemy dzięki temu równanie o parametrach:

Kolejnym krokiem w analizie, jest oszacowanie parametrów rozkładu składnika losowego pozwalające wnioskować o dobroci dopasowania modelu do danych empirycznych. Do pierwszego parametru należą średnie błędów szacunku estymatorów modelu. W tym celu należy obliczyć najpierw wariancje resztową
:

gdzie:

n - liczba obserwacji (dla naszego przykładu 30),

k - liczba parametrów modelu (dla naszego przypadku 2).

Obliczmy najpierw iloczyn macierzy Y^TY, który wynosi 70152. Iloczyn macierzy X^TY mamy już obliczony powyżej, dla przypomnienia :

pozostaje nam obliczyć iloczyn tej macierzy i wektora rozwiązań czyli
, a wynosi on: 68855. Przejdźmy do obliczenia

Możemy już teraz przejść do obliczenia średnich błędów szacunku modelu, które liczymy wg wzoru:

gdzie c_ji to elementy stojące na przekątnej macierzy (X^T X)^-1.

Obliczamy średnie błędy szacunku dla poszczególnych parametrów strukturalnych modelu:

• dla a₀

• dla a₁

Model nasz możemy, więc zapisać w postaci:

S_aj = (2,55) (0,14)

Wyznaczmy przedziały ufności dla parametrów modelu na poziomie istotności α=0,05 oraz dla n-k =28 stopni swobody. Z tablic rozkładu t-Studenta odczytujemy t_α =2,048. Przedzialy ufności kolejnych parametrów modelu liczymy z wzoru :

dla kolejnych parametrów naszego modelu uzyskujemy:

-9,1284<a₀<1,3164

Mówi nam to, że z prawdopodobieństwem 95%

2,6027<a₁<3,1753

Z prawdopodobieństwem 95%

W celu zbadania istotności parametrów strukturalnych modelu zakładamy, że składnik losowy ma rozkład normalny N(0,δ²) i weryfikujemy hipotezę

wobec alternatywnej

W tym celu wyznaczamy ze statystyki

t₀ dla a₀, które wynosi :

oraz t₁ dla a₁

Z tablic rozkładu t-Studenta dla n-k stopni swobody i α = 0,05 odczytujemy: t_0,05,28 = 2,048.

Przedstawmy tę sytuację na wykresie:

Wyniki mówią nam, że parametr a₀ dla którego przyjmujemy hipotezę H₀ jest statystycznie równy 0, oznacza to, że parametr ten nie ma wpływu na wielkość obrotów (przy t=0 , obroty są równe 0). Parametr a₁ jest istotnie różny od zera. Ma on wpływ na wielkość obrotów. Zapiszmy więc nasz model :

S_aj : (2,55) (0,14)

t_{j :} (-1,53) (20,64)

Aby sprawdzić dopasowanie oszacowanego modelu do danych rzeczywistych wyznaczamy współczynnik determinacji R² oraz odchylenie standardowe składnika resztowego modelu s.

Odchylenie standardowe reszt jest niczym innym jak pierwiastkiem kwadratowym z
czyli

w naszym przypadku wynosi ono 6,81 i mówi nam że przeciętne odchylenie wartości empirycznych od wartości rzeczywistych wynosi 6,81 tyś. zł.

Współczynnik determinacji obliczamy wg wzoru:

n - liczba obserwacji (30)

- średnia z macierzy = 40,867

Pozostałe wartości tego równania mamy już obliczone powyżej i po podstawieniu otrzymujemy

Model nasz jest więc bardzo dobrze dopasowany do danych empirycznych, bo wyjaśnia aż 93,53 % obserwacji. Posiadając obliczony współczynnik determinacji
możemy obliczyć współczynnik zbieżności
, który liczymy jako różnice : 1 - R² .

Niska wartość współczynnik zbieżności świadczy o dokładnym dopasowaniu modelu do danych empirycznych. Współczynnik ten mierzy tę część całkowitej zaobserwowanej zmienności zmiennej Y, która wynika z działania czynników losowych ( przypadkowych).

Współczynnik korelacji wielorakiej, to kolejna miara dopasowania modelu do danych empirycznych. Jest on pierwiastkiem kwadratowym z R². Dla naszego modelu:

Ostatnią miarą dopasowania modelu jest współczynnik zmienności losowej, czyli

Dla naszego modelu, uzyskujemy

Współczynnik V informuje nas , jaki procent średniego poziomu zaobserwowanej zmienności zmiennej objaśnianej Y stanowią odchylenia przypadkowe w danym równaniu trendu. Sytuacja ze statystycznego punktu widzenia jest tym lepsza im wartość V jest bliższa 0.

Współczynnik ten jest wyższy od wartości10%, co oznacza, że cechy wykazują zróżnicowanie statystycznie istotne.

Następnym etapem naszej analizy jest odpowiedz na pytanie: czy występuje autokorelacja?

Aby odpowiedzieć na to pytanie, zastosujmy statystykę Durbina-Watsona.

Musimy wykonać obliczenia pomocnicze, które przedstawiamy w tabeli poniżej.

t	yt	Yt	et	et^2	et-1	et-1^2	et -et-1	et et-1	(et -et-1)^2
1	8	-1,017	9,017	81,306	-	-	-	-	-
2	5	1,871	3,129	9,791	9,017	81,306	-5,888	28,214	34,669
3	15	4,76	10,24	104,858	3,129	9,791	7,111	32,041	50,566
4	13	7,648	5,352	28,644	10,24	104,858	-4,888	54,804	23,893
5	16	10,537	5,463	29,844	5,352	28,644	0,111	29,238	0,012
6	18	13,426	4,574	20,921	5,463	29,844	-0,889	24,988	0,790
7	17	16,314	0,686	0,471	4,574	20,921	-3,888	3,138	15,117
8	21	19,203	1,797	3,229	0,686	0,471	1,111	1,233	1,234
9	19	22,091	-3,091	9,554	1,797	3,229	-4,888	-5,555	23,893
10	23	24,98	-1,98	3,920	-3,091	9,554	1,111	6,120	1,234
11	25	27,868	-2,868	8,225	-1,98	3,920	-0,888	5,679	0,789
12	20	30,757	-10,757	115,713	-2,868	8,225	-7,889	30,851	62,236
13	24	33,645	-9,645	93,026	-10,757	115,713	1,112	103,751	1,237
14	27	36,534	-9,534	90,897	-9,645	93,026	0,111	91,955	0,012
15	22	39,422	-17,422	303,526	-9,534	90,897	-7,888	166,101	62,221
16	40	42,311	-2,311	5,341	-17,422	303,526	15,111	40,262	228,342
17	38	45,199	-7,199	51,826	-2,311	5,341	-4,888	16,637	23,893
18	45	48,088	-3,088	9,536	-7,199	51,826	4,111	22,231	16,900
19	51	50,977	0,023	0,001	-3,088	9,536	3,111	-0,071	9,678
20	47	53,865	-6,865	47,128	0,023	0,001	-6,888	-0,158	47,445
21	60	56,754	3,246	10,537	-6,865	47,128	10,111	-22,284	102,232
22	64	59,642	4,358	18,992	3,246	10,537	1,112	14,146	1,237
23	61	62,531	-1,531	2,344	4,358	18,992	-5,889	-6,672	34,680
24	63	65,419	-2,419	5,852	-1,531	2,344	-0,888	3,703	0,789
25	72	68,308	3,692	13,631	-2,419	5,852	6,111	-8,931	37,344
26	75	71,196	3,804	14,470	3,692	13,631	0,112	14,044	0,013
27	79	74,085	4,915	24,157	3,804	14,470	1,111	18,697	1,234
28	76	76,973	-0,973	0,947	4,915	24,157	-5,888	-4,782	34,669
29	90	79,862	10,138	102,779	-0,973	0,947	11,111	-9,864	123,454
30	92	82,751	9,249	85,544	10,138	102,779	-0,889	93,766	0,790
	-	-	-	1297,01	-	1211,4658	-	743,2836	940,6022

Dla zastosowania tej statystyki musimy zastosować poniższe wzory

• Estymator współczynnika autokorelacji

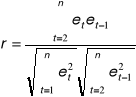
co po podstawieniu naszych danych z tabeli daje nam r = 0,593

• Statystyka Durbina-Watsona

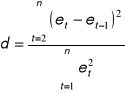
po podstawieniu danych z tabeli pomocniczej otrzymujemy d = 0,725.

Z tablic wartości krytycznych statystyki Durbina-Watsona, dla α=0,05 oraz n=30 i k=2 odczytujemy odpowiednie statystyki d_L=1,28 oraz d_u=1,57. Testujemy hipotezę

wobec hipotezy alternatywnej

Nanieśmy nasze dane na wykres.

Z powyższego wykresy wynika, że przyjmujemy hipotezę H₁. W naszym modelu mamy do czynienia z dodatnią autokorelacją składników losowych.

Jesteśmy zmuszeni wprowadzić macierz
, którą określamy jako

Jest to macierz, której na przekątnej wpisujemy 1+r² , jedynie pierwszy i ostatni element przekątnej to 1. w pola sąsiadujące z przekątną wpisujemy -r . W pozostałe pola wpisujemy 0. Nasz macierz Ω^-1 będzie zatem miała postać :

Macierz Ω^-1 ma wymiary 30 x 30 (ograniczony rozmiar tego arkusza uniemożliwia pokazanie całej macierzy). Uwzględniając macierz Ω^-1, wektor rozwiązań naszego modelu znajdziemy z wzoru:

Pierwszy człon tego równania
jest równy:

Drugi człon tego równania
jest równy:

Po wymnożeniu obu macierzy otrzymujemy nowy wektor rozwiązań modelu :

Ostatecznie model nasz możemy zapisać :

Poniżej przedstawiamy graficzną prezentację danych otrzymanych przy pomocy powyższego wzoru. Dane te zostały naniesione na wykres danych empirycznych.

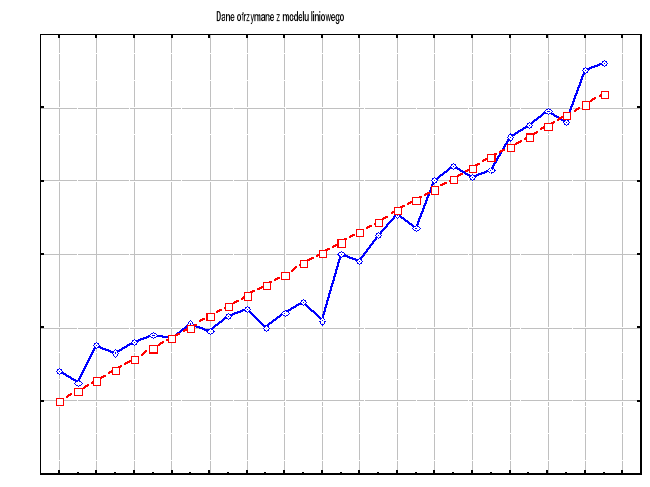
Ad.2

Zastąpmy zmienną x² nową zmienną x' uzyskując model postaci

Zmienna x' to nic innego jak nasze x podniesione do kwadratu.

Uzyskujemy, więc macierz X w postaci:

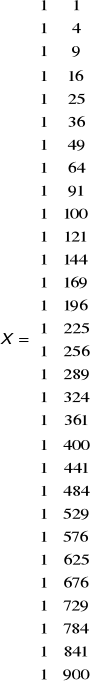
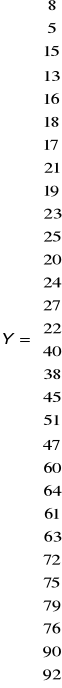
Model ten, tak ja i poprzedni możemy obliczyć MNK, czyli wg wzoru:

Wynik naszej operacji na macierzach (X^TX)^-1, jest macierz:

Macierz X^TY wygląda następująco:

Po wymnożeniu naszych macierzy, uzyskujemy wektor rozwiązań naszego modelu, czyli
:

Model nasz możemy zapisać w postaci:

Kolejnym krokiem będzie obliczenie wariancji resztowej
:

gdzie:

n - liczba obserwacji (dla naszego przykładu 30),

k - liczba parametrów modelu (dla naszego przypadku 2).

Iloczyn macierzy Y^TY wynosi 70152, natomiast iloczyn
- 69622,521. Po obliczeniu uzyskujemy, więc
=18,91.

Możemy już teraz przejść do obliczenia średnich błędów szacunku modelu, które liczymy- dla przypomnienia wg wzoru:

gdzie c_ji to elementy stojące na przekątnej macierzy (X^T X)^-1

Obliczamy średnie błędy szacunku dla poszczególnych parametrów strukturalnych modelu:

• dla a₀

• dla a₁

Model nasz możemy, więc zapisać w postaci:

S_aj = (1,2066) (0,0029)

Wyznaczmy, tak jak w poprzedniej analizie, przedziały ufności dla parametrów modelu na poziomie istotności α=0,05 oraz dla n-k =28 stopni swobody. Z tablic rozkładu t-Studenta odczytujemy t_α =2,048. Przedzialy ufności kolejnych parametrów modelu liczymy- dla przypomnienia z wzoru :

dla kolejnych parametrów naszego modelu uzyskujemy:

9,324<a₀<14,266

Mówi nam to, że z prawdopodobieństwem 95%

0,086<a₁<0,098

Z prawdopodobieństwem 95%

W celu zbadania istotności parametrów strukturalnych modelu zakładamy, że składnik losowy ma rozkład normalny N(0,δ²) i weryfikujemy hipotezę

wobec alternatywnej

W tym celu wyznaczamy ze statystyki

t₀ dla a₀, które wynosi :

oraz t₁ dla a₁

Z tablic rozkładu t-Studenta dla n-k stopni swobody i α = 0,05 odczytujemy: t_0,05,28 = 2,048.

Przedstawmy tę sytuację na wykresie:

Już z wykresu widzimy, że wszystkie nasze parametry modelu są istotnie różne od zera. Oszacowane przez nas parametry modelu mają istotny wpływ na wielkość obrotów. Zapiszmy nasz model w postaci:

S_aj : (1,2066) (0,0029)

t_j : (9,77) (31,72)

Aby sprawdzić dopasowanie oszacowanego modelu do danych rzeczywistych wyznaczamy współczynnik determinacji R² oraz odchylenie standardowe składnika resztowego modelu s.

Odchylenie standardowe reszt jest niczym innym jak pierwiastkiem kwadratowym z
czyli

w naszym przypadku wynosi ono 4,35 co oznacza, że przeciętne odchylenie wartości empirycznych od wartości rzeczywistych wynosi 4,35 tyś. zł. Obliczmy
, który obliczamy wg wzoru:

n - liczba obserwacji (30)

- średnia z macierzy = 40,867

Pozostałe wartości tego równania mamy już obliczone powyżej i po podstawieniu otrzymujemy

Model nasz jest więc bardzo dobrze dopasowany do danych empirycznych, bo wyjaśnia aż 97,36 % obserwacji. Posiadając obliczony współczynnik determinacji
możemy obliczyć

współczynnik zbieżności
, który liczymy jako różnice : 1 - R² .

Niska wartość współczynnik zbieżności świadczy o dokładnym dopasowaniu modelu do danych empirycznych.

Współczynnik korelacji wielorakiej, to kolejna miara dopasowania modelu do danych empirycznych. Jest on pierwiastkiem kwadratowym z R². Dla naszego modelu:

Ostatnią miarą dopasowania modelu jest współczynnik zmienności losowej, czyli

Dla naszego modelu, uzyskujemy

Współczynnik ten jest wyższy od wartości 10% co oznacza, że cechy wykazują zróżnicowanie statystycznie istotne.

A czy występuje autokorelacja? Zastosujmy statystykę Durbina-Watsona.

Musimy wykonać obliczenia pomocnicze, które prezentujemy w tabeli poniżej.

Dla obliczenia tej statystyki musimy zastosować poniższe wzory

• Estymator współczynnika autokorelacji

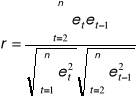
co po podstawieniu naszych danych z tabeli daje nam r = 0,123

• Statystyka Durbina-Watsona

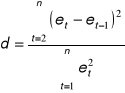
po podstawieniu danych z tabeli pomocniczej otrzymujemy d = 1,715.

Z tablic wartości krytycznych statystyki Durbina-Watsona, dla α=0,05 oraz n=30 i k=2 odczytujemy odpowiednie statystyki d_L=1,28 oraz d_u=1,57.

t	yt	Yt	et	et^2	et-1	et-1^2	et -et-1	et et-1	(et -et-1)^2
1	8	11,887	-3,887	15,109	-	-	-	-	-
2	5	12,163	-7,163	51,309	-3,887	15,109	-3,276	27,843	10,732
3	15	12,623	2,377	5,650	-7,163	51,309	9,54	-17,026	91,012
4	13	13,267	-0,267	0,071	2,377	5,650	-2,644	-0,635	6,991
5	16	14,095	1,905	3,629	-0,267	0,071	2,172	-0,509	4,718
6	18	15,107	2,893	8,369	1,905	3,629	0,988	5,511	0,976
7	17	16,303	0,697	0,486	2,893	8,369	-2,196	2,016	4,822
8	21	17,683	3,317	11,002	0,697	0,486	2,62	2,312	6,864
9	19	19,247	-0,247	0,061	3,317	11,002	-3,564	-0,819	12,702
10	23	20,995	2,005	4,020	-0,247	0,061	2,252	-0,495	5,072
11	25	22,927	2,073	4,297	2,005	4,020	0,068	4,156	0,005
12	20	25,043	-5,043	25,432	2,073	4,297	-7,116	-10,454	50,637
13	24	27,343	-3,343	11,176	-5,043	25,432	1,7	16,859	2,890
14	27	29,827	-2,827	7,992	-3,343	11,176	0,516	9,451	0,266
15	22	32,495	-10,495	110,145	-2,827	7,992	-7,668	29,669	58,798
16	40	35,347	4,653	21,650	-10,495	110,145	15,148	-48,833	229,462
17	38	38,383	-0,383	0,147	4,653	21,650	-5,036	-1,782	25,361
18	45	41,603	3,397	11,540	-0,383	0,147	3,78	-1,301	14,288
19	51	45,007	5,993	35,916	3,397	11,540	2,596	20,358	6,739
20	47	48,595	-1,595	2,544	5,993	35,916	-7,588	-9,559	57,578
21	60	52,367	7,633	58,263	-1,595	2,544	9,228	-12,175	85,156
22	64	56,323	7,677	58,936	7,633	58,263	0,044	58,599	0,002
23	61	60,463	0,537	0,288	7,677	58,936	-7,14	4,123	50,980
24	63	64,787	-1,787	3,193	0,537	0,288	-2,324	-0,960	5,401
25	72	69,295	2,705	7,317	-1,787	3,193	4,492	-4,834	20,178
26	75	73,987	1,013	1,026	2,705	7,317	-1,692	2,740	2,863
27	79	78,863	0,137	0,019	1,013	1,026	-0,876	0,139	0,767
28	76	83,923	-7,923	62,774	0,137	0,019	-8,06	-1,085	64,964
29	90	89,167	0,833	0,694	-7,923	62,774	8,756	-6,600	76,668
30	92	94,595	-2,595	6,734	0,833	0,694	-3,428	-2,162	11,751
Σ	-	-	-	529,789	-	523,055	-	64,546	908,642

Testujemy hipotezę

wobec hipotezy alternatywnej

Nanieśmy nasze dane na wykres.

W naszym przypadku (dla tego modelu ), przyjmujemy hipotezę H₀ - autokorelacja więc nie występuje. Model jest modelem zakończonym pod względem estymacji.

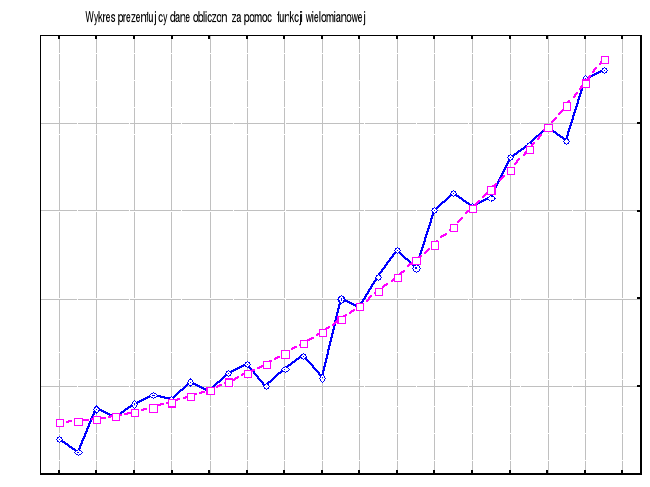
Nanieśmy jeszcze nasze dane uzyskane za pomocą ekstrapolacji naszą funkcją na wykres.

Dane te zostały naniesione na wykres danych empirycznych - dla porównania.

Ad.3

Aby móc wykorzystać MNK, musimy dokonać podstawień. Za zmienną x² podstawiamy x', uzyskując:

Macierz X i Y będą wyglądać następująco:

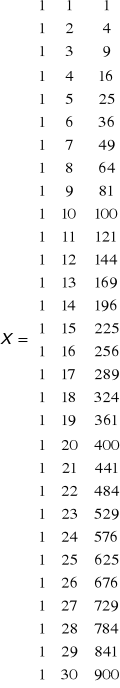
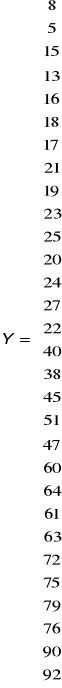
Po takim uporządkowaniu możemy zastosować już nasz wzór

Policzmy kolejno iloczyny macierzy:

1. 
   

2.

3.

Model nasz, przedstawiony za pomocą funkcji wielomianowej drugiego stopnia będzie miał postać:

Wariancja resztowa
:

gdzie:

n - liczba obserwacji (dla naszego przykładu 30),

k - liczba parametrów modelu (dla naszego przypadku 3).

Iloczyn macierzy Y^TY wynosi 70152, natomiast iloczyn
-69654,837. Po obliczeniu uzyskujemy, więc
=18,41 .

Możemy już teraz przejść do obliczenia średnich błędów szacunku modelu, które liczymy przypominamy wg wzoru:

gdzie c_ji to elementy stojące na przekątnej macierzy (X^T X)^-1

Obliczamy średnie błędy szacunku dla poszczególnych parametrów strukturalnych modelu:

• dla a₀

• dla a₁

• dla a₂

Model nasz możemy, więc zapisać w postaci:

S_aj = (2,517) (0,384) (0,0117)

Wyznaczmy, tak jak w poprzedniej analizie, przedziały ufności dla parametrów modelu na poziomie istotności α=0,05 oraz dla n-k =27 stopni swobody. Z tablic rozkładu t-Studenta odczytujemy t_α =2,052. Przedzialy ufności kolejnych parametrów modelu liczymy- dla przypomnienia z wzoru :

dla kolejnych parametrów naszego modelu uzyskujemy:

3,691<a₀<14,021

Mówi nam to, że z prawdopodobieństwem 95%

-0,292 <a₁<1,284

Z prawdopodobieństwem 95%

0,053 <a₂<0,101

a więc, z prawdopodobieństwem 95%

Zweryfikujmy hipotezę

wobec alternatywnej

W tym celu wyznaczamy ze statystyki

t₀ dla a₀, które wynosi :

oraz t₁ dla a₁

i t₂ dla a₂

Z tablic rozkładu t-Studenta dla n-k stopni swobody i α = 0,05 odczytujemy: t_0,05,27 = 2,052.

Przedstawmy tę sytuację na wykresie:

Wyniki mówią nam, że parametr a₁ dla którego przyjmujemy hipotezę H₀ jest statystycznie równy 0, oznacza to, że parametr ten nie ma wpływu na wielkość obrotów Parametr a₀ oraz a₂ są istotnie różne od zera. Mają one tym samym wpływ na wielkość obrotów. Zapiszmy nasz model w postaci :

S_aj : (2,517) (0,384) (0,0117)

t_j : (3,518) (1,292) (6,581)

Aby sprawdzić dopasowanie oszacowanego modelu do danych rzeczywistych wyznaczamy współczynnik determinacji R² oraz odchylenie standardowe składnika resztowego modelu s.

Odchylenie standardowe reszt jest niczym innym jak pierwiastkiem kwadratowym z
czyli

w naszym przypadku wynosi ono 4,29 co oznacza, że przeciętne odchylenie wartości empirycznych od wartości rzeczywistych wynosi 4,29 tyś. zł. Obliczmy
, który obliczamy wg wzoru:

n - liczba obserwacji (30)

- średnia z macierzy = 40,867

Pozostałe wartości tego równania mamy już obliczone powyżej i po podstawieniu otrzymujemy

Model nasz jest więc bardzo dobrze dopasowany do danych empirycznych, bo wyjaśnia aż 97,52 % obserwacji. Posiadając obliczony współczynnik determinacji
możemy obliczyć

współczynnik zbieżności
, który liczymy jako różnice : 1 - R² .

Niska wartość współczynnik zbieżności świadczy o dokładnym dopasowaniu modelu do danych empirycznych.

Współczynnik korelacji wielorakiej, to kolejna miara dopasowania modelu do danych empirycznych. Jest on pierwiastkiem kwadratowym z R². Dla naszego modelu:

Ostatnią miarą dopasowania modelu jest współczynnik zmienności losowej, czyli

Dla naszego modelu, uzyskujemy

Współczynnik ten jest wyższy od wartości 10% co oznacza, że cechy wykazują zróżnicowanie statystycznie istotne. Jest on jednak najniższy z wszystkich prezentowanych i liczonych powyżej.

Zastosujemy statystykę Durbina-Watsona.

Musimy wykonać obliczenia pomocnicze, które prezentujemy w tabeli poniżej.

t	yt	Yt	et	et^2	et-1	et-1^2	et -et-1	et et-1	(et -et-1)^2
1	8	9,429	-1,429	2,042	-	-	-	-	-
2	5	10,156	-5,156	26,584	-1,429	2,042	-3,727	7,368	13,891
3	15	11,037	3,963	15,705	-5,156	26,584	9,119	-20,433	83,156
4	13	12,072	0,928	0,861	3,963	15,705	-3,035	3,678	9,211
5	16	13,261	2,739	7,502	0,928	0,861	1,811	2,542	3,280
6	18	14,604	3,396	11,533	2,739	7,502	0,657	9,302	0,432
7	17	16,101	0,899	0,808	3,396	11,533	-2,497	3,053	6,235
8	21	17,752	3,248	10,550	0,899	0,808	2,349	2,920	5,518
9	19	19,557	-0,557	0,310	3,248	10,550	-3,805	-1,809	14,478
10	23	21,516	1,484	2,202	-0,557	0,310	2,041	-0,827	4,166
11	25	23,629	1,371	1,880	1,484	2,202	-0,113	2,035	0,013
12	20	25,896	-5,896	34,763	1,371	1,880	-7,267	-8,083	52,809
13	24	28,317	-4,317	18,636	-5,896	34,763	1,579	25,453	2,493
14	27	30,892	-3,892	15,148	-4,317	18,636	0,425	16,802	0,181
15	22	33,621	-11,621	135,048	-3,892	15,148	-7,729	45,229	59,737
16	40	36,504	3,496	12,222	-11,621	135,048	15,117	-40,627	228,524
17	38	39,541	-1,541	2,375	3,496	12,222	-5,037	-5,387	25,371
18	45	42,732	2,268	5,144	-1,541	2,375	3,809	-3,495	14,508
19	51	46,077	4,923	24,236	2,268	5,144	2,655	11,165	7,049
20	47	49,576	-2,576	6,636	4,923	24,236	-7,499	-12,682	56,235
21	60	53,229	6,771	45,846	-2,576	6,636	9,347	-17,442	87,366
22	64	57,036	6,964	48,497	6,771	45,846	0,193	47,153	0,037
23	61	60,997	0,003	0,000	6,964	48,497	-6,961	0,021	48,456
24	63	65,112	-2,112	4,461	0,003	0,000	-2,115	-0,006	4,473
25	72	69,381	2,619	6,859	-2,112	4,461	4,731	-5,531	22,382
26	75	73,804	1,196	1,430	2,619	6,859	-1,423	3,132	2,025
27	79	78,381	0,619	0,383	1,196	1,430	-0,577	0,740	0,333
28	76	83,112	-7,112	50,581	0,619	0,383	-7,731	-4,402	59,768
29	90	87,997	2,003	4,012	-7,112	50,581	9,115	-14,245	83,083
30	92	93,036	-1,036	1,073	2,003	4,012	-3,039	-2,075	9,236
	-	-	-	497,327	-	496,254	-	43,547	904,446

Dla obliczenia tej statystyki stosujemy poniższe wzory

• Estymator współczynnika autokorelacji

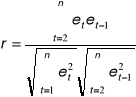
co po podstawieniu naszych danych z tabeli daje nam r = 0,087

• Statystyka Durbina-Watsona

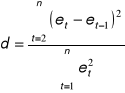
po podstawieniu danych z tabeli pomocniczej otrzymujemy d = 1,819.

Z tablic wartości krytycznych statystyki Durbina-Watsona, dla α=0,05 oraz n=30 i k=3 odczytujemy odpowiednie statystyki d_L=1,21 oraz d_u=1,65. Testujemy hipotezę

Również w tym przypadku przyjmujemy hipotezę H₀ - autokorelacja, więc nie występuje. Model jest modelem zakończonym pod względem estymacji.

Nanieśmy jeszcze nasze dane uzyskane za pomocą ekstrapolacji naszą funkcją na wykres.

Dane te zostały naniesione na wykres danych empirycznych - dla porównania.

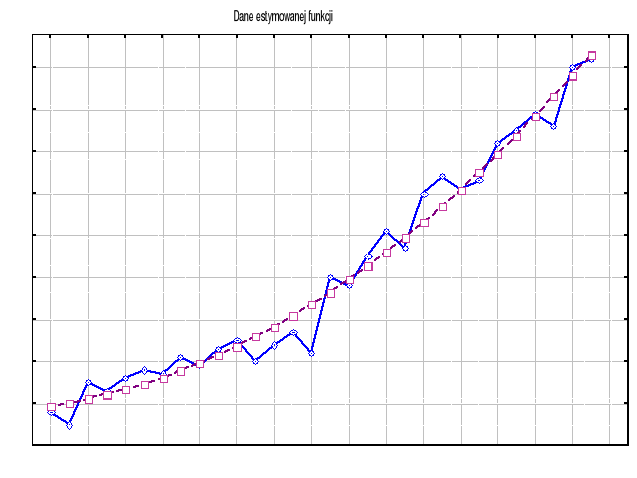
Porównajmy uzyskane wyniki:

Parametry
	2,55	1,2066	2,517
	0,14	0,0029	0,384
	-	-	0,0117
	0,9353	0,9736	0,9752
	0,0647	0,0264	0,0248
R	0,9671	0,9867	0,9875
V	0,1666	0,1064	0,105
s	6,81	4,35	4,29

Wadą pierwszego modelu jest występowanie autokorelacji składników losowych. Występuje tu też wyższy niż w innych prezentowanych modelach współczynnik zmienności losowej V.

Ogólne miary dopasowania świadczą o tym, że to trzeci model wielomianowy stopnia drugiego jest najlepiej dopasowany do danych empirycznych. Dla tego modelu 2,48% zmienności zmiennej objaśnionej nie zostało wyjaśnione przez model, jest to wielkość najniższa spośród tych trzech modeli. Model ten również ma najniższy błąd standardowy s czyli przeciętne odchylenie ilości rzeczywistej od ilości wyznaczonej na podstawie modelu. Z tego powodu model ten w postaci:

uznaliśmy za dobry i wybraliśmy go jako końcowy i właściwy efekt naszej pracy.

Dla zainteresowanych, podajemy poniżej wykres programu Excel z naniesioną linią trendu dla funkcji wielomianowej stopnia 6.

Dla tego modelu R² = 0,9838. Wydaje się nam, że model przez nas wybrany z funkcją wielomianową jest bardzo dobrym modelem i wybór dokonany przez nas jest wyborem słusznym.

TABLICE DURBINA-WASTONA dla poziomu istotności 0,05 (służą do badania autokorelacji, oznaczenie: d lub DW).

1. Tablice od n=15.  (poniżej tablice dla n=6)

Oznaczenia:
n- liczba obserwacji.
k- liczba zmiennych w modelu.

2. Tablice od n=6.

DYSTRYBUANTA ROZKŁADU STUDENTA (t-Studenta).

Tablice Dystrybuanty Rozkładu Normalnego (oznaczenie U lub Z).

1

H₁

H₁

H₀

t_j

t₁=20,64

t₀=-1,53

t_α

-t_α

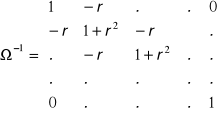
t₁=31,72

t₀=9,77

t_α

-t_α

t_j

H₀

H₁

H₁

t₁=1,292

t₀=3,518

t_α

-t_α

t_j

H₀

H₁

H₁

t₂=6,581

W 2 kolumnie wartości t

W 1 kolumnie same jedynki

Do macierzy Y podstawiamy wartości Y_t

W 1 kolumnie same jedynki

W 2 kolumnie wartości t²

Do macierzy Y podstawiamy wartości Y_t

W 1 kolumnie same jedynki

W 2 kolumnie wartości t

W 3 kolumnie wartości t²

Do macierzy Y podstawiamy wartości Y_t

---