PRZYKŁAD 1

Zaprojektować zbrojenie belki prostokątnej na zginanie.

Dane:

M_Ed = 170 kN⋅m = 0,170 MN⋅m

h = 0,45 m, b = 0,25 m,

Przyjęto:

beton C30/37 (B37) f_cd = 30/1,4 = 21,4 MPa

stal B500SP klasy C f_yd = 500/1,15 = 435 MPa

klasa konstrukcji S4, klasa ekspozycji XC3

φ_max = 20 mm

- Określenie nominalnej grubości otuliny

c_min = max{c_min,b = φ; c_min,dur; 10mm} =

= max{20mm; 25mm; 10mm} = 25 mm

c_dev = 10 mm

c_nom = c_min + c_dev = 25 + 10 = 35 mm

- Obliczenie a₁

przyjmując φ_strzem = 8 mm

a₁ = 35 + 8 + 0,5 ⋅ 20 = 53 mm

- Obliczenie d

d = 0,45 - 0,053 = 0,397 m

przyjęto d = 0,40 m

Obliczenie przekroju zbrojenia A_s1

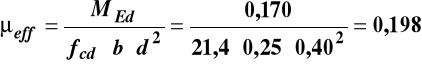
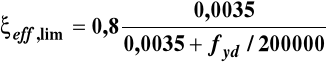
= 0,50

przekrój jest pojedynczo zbrojony

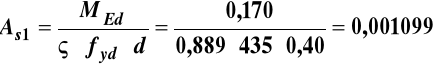
m² =10,99 cm²

przyjęto 4 φ 20

As1 = 12,57 cm^2

Minimalny przekrój zbrojenia

A_s1,min = 0,0013bd = 0,0013 ⋅ 0,25 ⋅ 0,40 = 0,000130 m² =1,30 cm²

A_s1,min = 0,26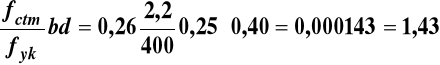
cm²

Stopień zbrojenia

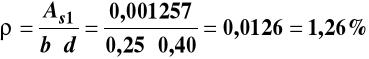
Rozmieszczenie zbrojenia w przekroju obliczanej belki

s_l ≥ φ

s_l ≥ (d_g + 5 mm)

s_l ≥ 20 mm

Rozstaw prętów (patrz EC2 p. 8.2)

Rozstaw prętów zbrojenia powinien umożliwiać właściwe ułożenie i zagęszczenie betonu zapewniające uzyskanie odpowiedniej przyczepności zbrojenia.

Odległość w świetle (w kierunku poziomym i pionowym) między pojedynczymi równoległymi prętami lub między poziomymi warstwami równoległych prętów nie powinna być mniejsza od maksymalnej średnicy pręta pomnożonej przez k₁, od (d_g + k₂) milimetrów i od 20 milimetrów (d_g oznacza maksymalny wymiar ziaren kruszywa).

Zalecane wartości k₁ = 1 oraz k₂ = 5 mm

PRZYKŁAD 2

Sprawdzić nośność przekroju zginanego.

Dane:

h = 0,50 m, b = 0,25 m, a₁ = 0,05 m, d = 0,45 m

beton C20/25 (B25) f_cd = 20/1,4 = 14,3 MPa

stal A-II f_yk = 355 MPa f_yd = 355/1,15 = 310 MPa

Szukane:

M_Rd - nośność przekroju

• Obliczenie ξ_eff

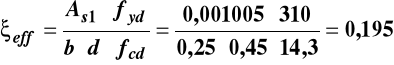
• Obliczenie x_eff

m

• Określenie nośności przekroju

M_Rd = f_cd ∙ b ∙ x_eff (d - 0,5x_eff) =

= 14,3 ∙ 0,25 ∙0,088 (0,45 - 0,5 ∙ 0,088) = 0,12772 = 127,72 kNm

lub

M_Rd = f_yd ∙ A_s1 (d - 0,5x_eff) =

= 310 ∙ 0,001005 (0,45 - 0,5 ∙ 0,088) = 0,12650 = 126,50 kNm

PRZYKŁAD 3

Zaprojektować zbrojenie w przęśle belki swobodnie podpartej.

(W przykładzie przeanalizowano wpływ zmiany wysokości użytecznej belki d na wielkość potrzebnego przekroju

zbrojenia A_s1)

Dane:

l_eff = 6,9 m

h = 0,60 m, b = 0,30 m,

obciążenie obliczeniowe (g + q) = 80,0 kN/m

Przyjęto:

beton C30/37 (B37) f_cd = 30/1,4 = 21,4 MPa

stal B500SP f_yd = 500/1,15 = 435 MPa

klasa ekspozycji XC2, klasa konstrukcji S3,

z tabl. 4.4N c_min,dur = 20 mm

c_min,b ≥ φ przyjęto φ = 20 mm,

Δc_dev = 10 mm

Szukane: A_s1

• Grubość otuliny

c_nom = c_min + Δc_dev

c_nom = 20 + 10= 30 mm

• Obliczenie a₁ (założono ułożenie zbrojenia w jednym rzędzie)

a₁ = c_nom + φ_strzem + 0,5 φ_zbroj przyjęto φ_strzem = 6 mm

φ_zbroj = 20 mm

a₁ = 30 + 6 + 0,5 ⋅ 20 = 46 mm

- Wysokość użyteczna

d = h - a₁ = 0,60 - 0,046 = 0,554 m

- Obliczeniowy moment zginający

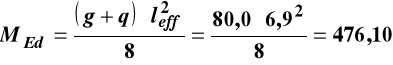
kNm

- Obliczenie przekroju zbrojenia A_s1

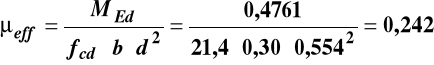
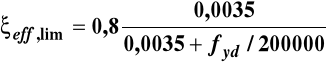
= 0,50

przekrój pojedynczo zbrojony

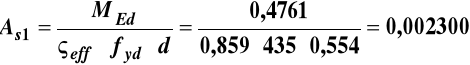
m²

=23,00 cm²

przyjęto 8 φ 20

As1 = 25,12 cm^2

Konieczne jest ułożenie zbrojenia w dwóch rzędach

• Obliczenie rzeczywistej wysokości użytecznej przekroju d_rz

a₁ = c_nom + φ_strzem + φ_zbroj + 0,5 s_l = 25 + 6 + 20 + 0,5 ⋅ 20 = 61 mm

d_rz = 0,60 - 0,061 = 0,539 m

• Obliczenie potrzebnego przekroju zbrojenia A_sx dla

rzeczywistej wysokości użytecznej przekroju d_rz

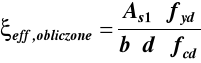
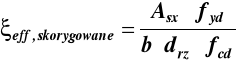
czyli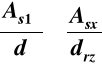

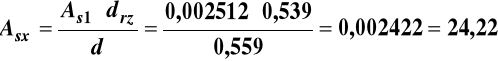
cm² <

25,12cm²

Wykazano, że przyjęte zbrojenie 8 φ 20, A_s1 = 25,12 cm² obliczone przy założeniu układania prętów w jednym rzędzie jest wystarczające w przypadku zmniejszenia wysokości użytecznej d wynikającej z konieczności układania prętów w dwóch rzędach.

PRZYKŁAD 4

Zaprojektować belkę żelbetową swobodnie opartą na murze dla następujących danych:

- rozpiętość w świetle podpór l_n = 6,6 m

- całkowite obciążenie obliczeniowe g + q = 20,0 kN/m

- beton klasy C25/30, (B30) f_cd = 25/1,4 = 17,8 MPa

- stal klasy C, gatunek B500SP f_yd = 500/1,15 = 435 MPa

- klasa ekspozycji XC2/XC3, klasa konstrukcji S3,

z tabl. 4.4N c_min,dur = 20 mm

c_min,b ≥ φ przyjęto φ = 20 mm,

Δc_dev = 10 mm

- rozpiętość obliczeniowa

l_eff = l_n + a₁ + a₂

a₁ = a₂ = min{0,5t; 0,5h}

t - głębokość oparcia t = 0,25 m

h - wysokość belki przyjęto wstępnie h = 0,50 m

l_eff = 6,6 m + 0,125 + 0,125 = 6,85 m

- moment od obciążeń obliczeniowych

M_Ed = 0,125 ( g + q) l_eff² = 0,125 ∙ 20,0 ∙ 6,85² = 117,3 kNm

- grubość otuliny

c_nom = c_min + Δc_dev = 20 + 10 = 30 mm

- określenie a₁ czyli odległości od krawędzi rozciąganej do środka

ciężkości zbrojenia

wstępnie przyjęto:

φ_zbroj = 20 mm

φ_strzem = 6 mm

a₁ = c_nom + φ_strzem + 0,5 φ_zbroj = 30 + 6 + 10 = 46 mm

Wstępne przyjęcie wymiarów belki

- założono:

szerokość belki b = 0,20 m

ekonomiczny stopień zbrojenia ρ = 1,0 %

- obliczenie użytecznej wysokości belki „d”

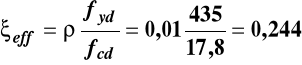
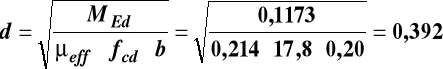
m

= 0,392 + 0,046 = 0,438 m

(zaleca się przyjmować wymiary belek monolitycznych ze stopniowaniem co 5 cm)

Ostatecznie do dalszych obliczeń przyjęto h = 0,45 m,

czyli

d = h - a₁ = 0,45 - 0,046 = 0, 404 m = 0,40m

Obliczenie przekroju zbrojenia rozciąganego A_s1

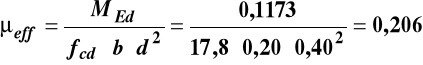
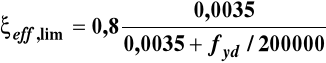
= 0,50

ξ _eff ≤ ξ_eff,lim - przekrój pojedynczo zbrojony

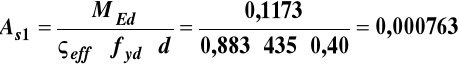
m² =7,63 cm²

Przyjęto 3 φ 18 , As = 7,63 cm^2

Można także przyjąć 4 φ 16, A_s = 8,04 cm²

Stopień zbrojenia przekroju

%

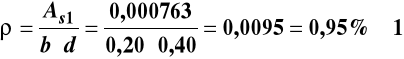
Sprawdzenie minimalnego pola przekroju zbrojenia podłużnego

z warunków normowych:

A_s,min = 0,0013bd = 0,0013 ⋅ 0,20 ⋅ 0,40 = 0,000104 m² =1,04 cm²

A_s,min = 0,26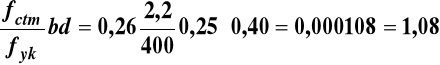
cm²

---