Ćwiczenia statyka 4 - 15 -
Zadanie 13
Do tarczy hamulca taśmowego przyłożony jest moment M. Jaką siłę P należy przyłożyć do końca dzwigni AC tego hamulca (rys.13), aby utrzymać w uwnowadze tarczę hamulca. Do obliczeń przyjąć następujące dane: M = 10Nm, R = 15cm, a = 1m, b = 20cm, α = 200, β = 320.
Współczynnik tarcia ślizgowego taśmy o tarczę hamulca wynosi μ = 0,23.
M
900- β 900
B C x
A
b α
a P
Rys.13
Rozwiązanie
Równowaga dzwigni AC (rys.13a)
y
RA RB
A B C x
b α
a P
Rys.13a
Soma momentów sil względem punktu A równa się zero
Moment od siły RA względem A równa się zero
Wartość momentu od siły RB względem A równa się rBRB sinαRB = bRBsin900 =bRB (rys.13b)
RB
αRB = 900
A rB B x
b Rys.13b
Wartość momentu od siły P względem A równa się rAP sinαP = aPsin(2700 +α)= -Pacosα
(rys.13c)
αP = 2700 + α
rP C x
A
a
P Rys.13c
ostatecznie
![]()
stąd ![]()
(a)
Równowaga tarczy hamulca - 16 -
R0
M
0
R
900- β
A B
S1 S2 = - RB S2 = RB Rys.13d
Suma momentów względem 0
![]()
(b)
Zależność miedzy S1 i S2 jest określona wzorem ![]()
(patrz wzór 5.15 strona 87
Statyka i Wytrzymałość Matriałów autor Jan Misiak) gdzie w naszym przypadku α = π + β
stąd ![]()
Po podstawieniu S1 do (b) i uwzględnieniu że S2 = RB
![]()
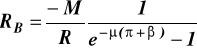
uwzględniając (a)
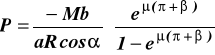
po podstawieniu danych i uwzględnieniu ze
β = 0,558 radiana czyli ![]()
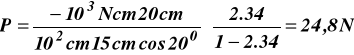
Zadanie 14
Plytę o masie m = 200kg ustawiono na dwóch symetrycznie ustawionych wałkach o promieniu r = 5 cm, mogących toczyć się po poziomym podłożu. W celu przesunięcia płyty przyłożono do niej poziomą siłę P. Należy wyznadzyć, jaki warunek musi spełnioać wartość liczbowa tej siły, jeżeli współczynnik przy toczeniusię wałków po płycie f1 = 0.05 cm, a wałków po podłożu f2 = 0,1 cm. Masy wałków pominąć (rys.14).
P
a a
0 Q 0
Rys.14
Rozwiązanie - 17 -
Siły działające na płytę (rys.14a)
y
N1 N2
P x
01
T1 Q T2 Rys.14a
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Siły działające na wałek (rys.14b) y N1g = -N1 N1g = N1 = N
f1
Tig = - T1
T1g = T1 = T
0
r
A
T1d
N1d
f2 Rys.14b
![]()
![]()
![]()
(a)
Wstawiając do (a) otrzymane wartości T i N mamy ![]()
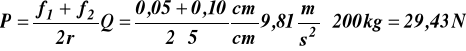
Jest to warunek równowagi. Jeśli chcemy wywołac ruch to P > 29,43 N.
Zadanie 15
Wyznaczyć współrzędne środka ciężkości powierzchni wycinka koła o promieniu R = 10cm
i kącie środkowym 2α = 680 (rys.15).
x A
R
α
0 y
α
B Rys.15
Rozwiązanie - 18 -
y
y
R A
A Rd*
B B
* yS S
0 x dA
α
d*
xS
0 x
Rys.15a Rys.15b
Pole elementarnego trójkąta 0AB ![]()
Połażenie środka ciężkości elementarnego trójkąta 0AB jest w punkcie S w 1/3 wysokości od podstawy AB stąd 0S =2R/3
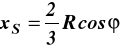
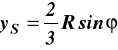
Momenty statyczne względem osi x, y trójkąta 0AB
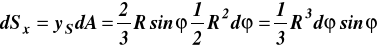
(a)
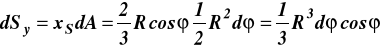
(b)
Momenty statyczne względem osi x, y oraz pole analizowanej powierzchni
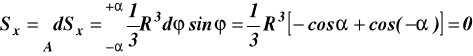
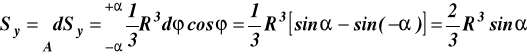
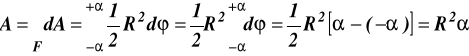
Położenie środka ciężkości określamy z wzorów wyprowadzonych w książce Statyka i Wytrzymałość Materiałów strona 130 wzór (7.25) autot Jan Misiak.
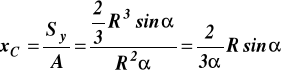
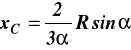
![]()
![]()
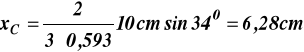
Zadanie 16 - 19 -
Wyznaczyć położenie środka ciężkości figury płaskiej podanej na rysunku 16.
y
R C
*
0 x Rys.16
Rozwiązanie
Aby to zadanie rozwiązać wykorzystujemy rysunek 15b, oraz wzory na (a) i ((b) zadania15
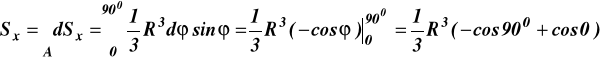
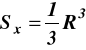
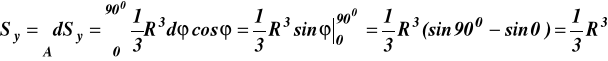
![]()
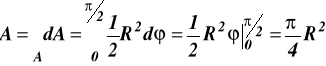
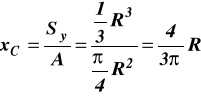
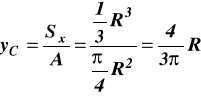
(c)
Zadanie 17
Znależć położenie środka ciężkości figury płaskiej pokazanej na rysunku 17. Dane prostokąta a = 39cm, h = 22 cm, promień otworu R = 6 cm.
y a
R
h
x Rys.17
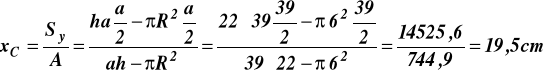
![]()
Wyszukiwarka