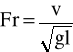
1) Różnice między zjawiskami podobnymi i analogicznymi

Zjawiska podobne - tego samego rodzaju, określone jednakowymi równaniami, zarówno, w formie analitycznej jak i w treści fizycznej.

Zjawiska analogiczne - określone takimi samymi równaniami w formie analitycznej ale różniącymi się co do treści fizycznej.

2) Podać i omówić sens fizyczny liczb Fr, Re ,We.

Fr - liczba Froude'a jest miarą stosunku siły bezwładności (składowej konwekcyjnej) do siły ciężkości, często przedstawiana w postaci pierwiastka kwadratowego z ilorazu tych sił.

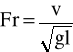
Re - liczba Reynoldsa wyraża stosunek składowej konwekcyjnej siły bezwładności do siły tarcia w płynie. Jest stosowana między innymi do badania rodzaju ruchu cieczy. Stanowi główne kryterium modelowania hydraulicznego, jeżeli dominującymi w zjawisku są siły wynikające z lepkości płynu.

We - liczba Webera wyznacza warunek zachowania wzajemnego stosunku sił wynikających z napięć powierzchniowych i śił bezwładności.

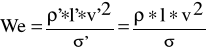
3) Wskazać na trudności w modelowaniu zjawisk.

Modelowanie zjawisk staje się coraz trudniejsze, wraz ze wzrostem kryteriów podobieństwa które chcieli byśmy spełnić. Na przykład zakładamy rozmiar modelu α_L = 1/100 i chcemy aby spełnione były kryteria Froude'a i Reynoldsa.

Kryterium Froude'a -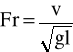
=
; g = g' (przyśpieszenie ziemskie jest takie same);

l / l'= 1/100 to v / v'=1/10

Kryterium Reynoldsa -
;
(taka sama ciecz w modelu co w rzeczywistości)

l / l'= 1/100 to v / v'=1/100 stąd w jednym modelu nie jesteśmy w stanie użyć obydwu kryteriów podobieństwa, chyba, że model będzie w skali 1:1.

4) Wyprowadzić Żukowskiego wzór na przyrost ciśnienia w uderzeniu hydraulicznym.

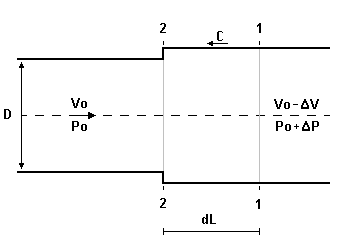
Zmiany gęstości i pola przekroju poprzecznego są na tyle małe w porównaniu ze zmianami prędkości i ciśnienia iż można je pominąć.

Rozpatrujemy odcinek przewodu o długości dL i średnicy D. Fala ciśnienia w chwili t znajduje sie w przekroju 1 i po czasie dt dociera do przekroju 2 ( c =dL/dt, c - prędkość fali). W czasie dt warunki jakie panowały na prawo od przekroju 1 ustaliły się na odcinku dL przewodu i wynoszą:

v = v₀ - Δv ; p = p₀ + Δp ; ρ = ρ₀ + ρΔ ; A = A₀ + ΔA, na lewo od przekroju 2 warunki nie uległy zmianie i wynoszą v₀, p₀, ρ₀, A_0. Stosując równanie ruchu (pędu i popędu) do cieczy zawartej między przekrojami 1 i 2 można zapisać:

przyjmując, że A₀ = A i wstawiając za dL dt *c otrzymujemy :

Δp = ρ * ΔV * c

Gdy prędkość spada to rośnie ciśnienie, maksymalne ciśnienie występuje gdy prędkość spadnie do zera.

5) Pojęcie lepkości Newtona i wpływ temperatury na lepkość dynamiczną cieczy.

Lepkością nazywamy zdolność płynu do przenoszenia naprężeń stycznych, przy wzajemnym przemieszczaniu się jego elementów z różnymi prędkościami.

τ - naprężenia styczne, T- siła tarcia , A - powierzchnia, μ - dynamiczny współczynnik lepkości płynu [kg/m*s], dv - zmiana prędkości na drodze dn. Zgodnie z powyższym wzorem zachowują się tylko płyny Newtonowskie (zaliczamy do nich większość cieczy i wszystkie gazy).

- kinematyczny współczynnik lepkości [m² / s].

Lepkość płynów newtonowskich zależy głównie od temperatury i nieznacznie od ciśnienia.

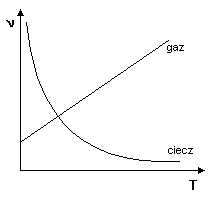
Dla cieczy lepkość maleje ze wzrostem temperatury, dla gazów odwrotnie. Wynika to z różnych przyczyn powstawania oporów tarcia w obu ośrodkach. Źródłem sił stycznych między dwiema poruszającymi się warstwami cieczy są siły spójności (adhezji), które maleją wraz ze wzrostem temperatury. W gazie siły spójności nie odgrywają większej roli siły tarcia powstają w wyniku przenoszenia pędu między sąsiednimi warstwami (bezwładny ruch molekularny). Wraz ze wzrostem temperatury rośnie energia kinetyczna ruchu postępowego cząstek a tym samym intensywność wymiany pędu.

6) Porównać naprężenia newtonowskie i turbulentne.

Naprężenia newtonowskie są to naprężenia wywołane przez lepkość. Naprężenia turbulentne są wywołane ruchem pulsacyjnym płynu.

7) Podstawowe definicje : rodzaje sił w mechanice płynów.

Siły masowe - wynikają z oddziaływania zewnętrznego pola sił, są proporcjonalne do całej masy płynu. Można do nich zaliczyć siły: ciężkości, bezwładności, odśrodkową Miarą sił masowych jest jednostkowa siła masowa F_jm

Siły powierzchniowe - działają na powierzchni wydzielonej masy płynu i są proporcjonalne do tej powierzchni. Do sił powierzchniowych należy zaliczyć siły tarcia i parcia hydrostatycznego (napięcie powierzchniowe - szczególny przypadek). Miarą sił powierzchniowych jest jednostkowa siła powierzchniowa F_jA

8) Omówić różniczkowe równanie ciągłości i jego modyfikacje

Różniczkowe równanie ciągłości jako realizacja prawa zachowania masy:

Dla ruchu ustalonego płynu nieściśliwego (ρ = const) równanie można zapisać:

Różniczkowe równanie ruch płynu lepkiego - równanie Naviera - Stokesa

gdzie:

- przedstawia siły bezwładności

- siły masowe zewnętrzne

- siły powierzchniowe normalne

- wpływ sił tarcia

- wpływ sił parcia, związany ze ściśliwością

Gdy płyn jest nieściśliwy (
), równanie przyjmuje postać

Gdy płyn jest nielepki (
) , równanie sprowadza się do:

Gdy płyn znajduje się w stanie spoczynku względem układu współrzędnych (v=0), to równanie upraszcza się do postaci

9) Wykazać, że w ruchu potencjalnym siły masowe są ortogonalne.

Praca sił masowych na powierzchni jednakowych ciśnień jest równa 0, bo siła nie da pracy jeżeli będzie zorientowana normalnie.

10) Narysuj i wyprowadź równanie na manometr różnicowy dla ρ < ρ_cm i ρ > ρ_cm.

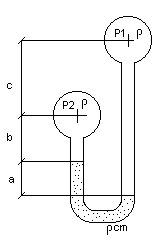
A) ρ < ρ_cm

p₁ + ρ * g * (a + b + c) = p₂ + ρ_cm * g * a + ρ * g * b p₁ - p₂ = Δp

Δp = ρ_cm* g * a - ρ * g * (a + c)

Δp = (ρ_cm - ρ) * g * a - ρ *g*c

B) ρ > ρ_cm

p₁ - ρ * g * (a +b) = p₂ - ρ * g * (c + b) - ρ_cm * g * a p₁ - p₂ = Δp

Δp = ρ * g * a - ρ * g * c - ρ_cm * g * a

Δp = (ρ - ρ_cm) * g * a - ρ * g * c

11) Wyprowadzić wzór na parcie na powierzchnię płaską

Przyjmujemy że: oś x przebiega wzdłuż przecięcia ściany zbiornika ze zwierciadłem cieczy, oś y prostopadle do osi x, w płaszczyźnie ściany oś z pionowo w dół.

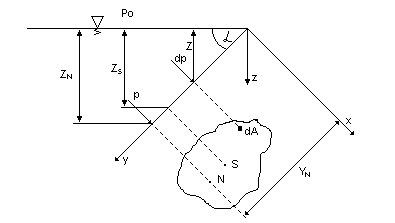
Parcie P jako wypadkowa parć elementarnych prostopadłych do elementów powierzchni dA, jest skierowane normalnie do tej płaszczyzny. Ciśnienie w dowolnym punkcie cieczy znajdującej się w stanie bezwzględnego spoczynku wynosi:

Elementarne parcie hydrostatyczne na element powierzchni dA o współrzędnych x,y,z, wynosi:

Całkowite parcie na pole A jest równe:

Uwzględniając zależności

możemy zapisać że:

czyli:

Jeżeli na powierzchnię A od zewnątrz działa siła wywołana ciśnieniem p₀ to

12) Wykazać, że środek parcia na powierzchnie płaską działa poniżej środka ciężkości

;

;

;

;

;

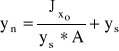
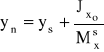
Ze wzoru wynika, że środek parcia jest położony poniżej środka ciężkości rozpatrywanej powierzchni A.

13) Czy siła wyporu jest siłą powierzchniową czy masową?

Siła wyporu jest wypadkową sił parcia pionowego, czyli jest siłą powierzchniową.

14) Wyprowadzenie i założenia do wzoru na wysokość metacentryczną

Wysokość metacentryczna określa równowagę ciał częściowo zanurzaonych

Rysunek 4.22 strona 78.

Założenia: środek ciężkości (S_c) leży powyżej środka wyporu (S_w) i przyłożona zewnętrzna siła powoduje wychylenie ciała o niewielki kąt Δφ, którego wartość wyrażona w radianach jest w przybliżeniu równa wartości sinusa i tangensa tego kąta (Δφ ≈ sin Δφ ≈ tg Δφ ).

ε = (m + a) sin Δφ = (m + a) Δφ

Wynurzona i zanurzona część ciała podzielone zostały na elementarne słupki. W odległości y od osi obrotu wysokość słupka o powierzchni podstawy dA wynosi y * tg Δφ, a objętość dA * y * tg Δφ ≈ dA * y * Δφ. Na słupek działa elementarny wypór

dW = γ * dA * y * Δφ

którego moment względem osi obrotu O wynosi

dW = γ * dA * y² * Δφ

Całkowity moment od pary sił jest sumą momentów od elementarnych sił wyporu

Porównując oba momenty sił (W' = W) można zapisać:

W * ε = γ * Δφ * J , W = γ * V

Podstawiając za ε uprzednio wyznaczoną wartość, otrzymujemy

gdzie: J - moment bezwładności płaszczyzny pływania względem osi obrotu, V - objętość części zanurzonej, a - odległość między środkiem ciężkości a środkiem wyporu (dodatnia gdy S_c leży powyżej S_w)

15) Czy na ciało zanurzone zawsze działa wypór?

Nie zawsze. Siła wyporu nie działa w wypadku gdy pod ciałem nie znajduje się woda, czyli gdy ciało szczelnie przylega do dna.

16) Porównać badanie ruchu metodą Lagrange'a i metoda Eulera.

Metoda Lagrange'a (analizy wędrownej) polega na badaniu właściwości fizycznych i opisie poruszającego się elementu płynu. W tym celu dokonujemy wyboru cząstki np. po przez opisanie współrzędnych położenia a, b, c dla chwili t₀, a następnie jej śledzenie w kolejnych chwilach t. W wyniku zastosowanej metody otrzymuje się opis ruchu płynu w postaci

f=f(a,b,c,t)

gdzie f jest współrzędną położenia lub własnością płynu w chwili t.

Współrzędne położenia elementu płynu w kolejnych chwilach czasowych, wyrażające parametryczne równanie toru cząstki, określają następujące równania :

x = x (a, b, c, t) y = y (a, b, c, t) z = z (a, b, c, t)

Składowe prędkości poszczególnych elementów płynu wynoszą:

,
,
,

a składowe przyśpieszeń

Inne parametry wyraża się podobnie jak równanie toru np. p = p (a, b, c, t); ρ = ρ (a, b, c, t)

Metoda Eulera (analizy lokalnej) opisuje zmiany wielkości fizycznych płynu w poszczególnych punktach przestrzeni w której odbywa się ruch. Metoda ta polega więc na badaniu pól wielkości fizycznych a nie indywidualnych cech poszczególnych elementów płynu. W wyniku jej zastosowania otrzymujemy opis ruchu

V_x = V_x(x, y, z, t); V_y = V_y(x, y, z, t); V_y = V_y(x, y, z, t)

p = p (x, y, z, t); ρ = ρ (x, y, z, t)

Dla zmiennego pola prędkości przyśpieszenie możemy opisać wzorem:

Jeżeli:
to

; gdzie:

- pochodna konwekcyjna, związana z przesunięciem się elementu po jego torze;
- pochodna lokalna;

- pochodna substancjalna prędkości, wyraża rzeczywiste przyśpieszenie.

17) Kiedy tor pokrywa się z linią prądu?

W ruchu ustalonym, czyli wtedy gdy funkcja f zależy jedynie od położenia a nie zależy od czasu.

18) Pojęcie objętości kontrolnej.

Jest to objętość ograniczona powierzchnią kontrolną. Powierzchnia kontrolna - nieruchoma zamknięta lub otwarta powierzchnia przeprowadzona w polu prędkości.

19) Interpretacja geometryczna i fizyczna równania Bernoulliego.

Równanie to otrzymujemy po scałkowaniu równania Eulera w polu grawitacyjnym, w ruchu ciągłym i ustalonym
i przy stałej gęstości.

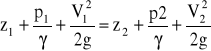
każdy za składników równania ma wymiar w metrach

z - wysokość położenia ponad poziomem porównawczym

- wysokość ciśnienia

- wysokość prędkości Cała praca sił ciężkości oraz sił parcia powoduje zmianę energii kinetycznej cieczy doskonałej. Inaczej mówiąc: suma wysokości położenia, ciśnienia i prędkości w każdym przekroju strugi cieczy doskonałej w ruchu ustalonym, w jednorodnym polu grawitacyjnym jest prędkością stałą. Suma ta jest zwana wysokością energii.

20) Założenia i wnioski do równania Hagena - Poiseuille'a

Założenia:

- ruch jest ciągły i ustalony

- płyn jest nieściśliwy ρ = const

- tory są równoległe do osi x (ruch ustalony to linie prądu też)

- pomijamy składowe jednostkowe sił masowych X, Y, Z

Wnioski:

- wydatek Q jest wprost proporcjonalny do spadku ciśnienia i odwrotnie proporcjonalny do

długości przewodu

- rozkład prędkości w przekroju poprzecznym przewodu kołowego jest paraboliczny (prędkość

max. występuje w osi przewodu)

-Występuje liniowy rozkład naprężeń stycznych

21) Cechy ruchu laminarnego:

- energia przekazywana ruchem pulsacyjnym jest nieduża i przepływ jest stateczny

- nie zachodzi wymiana płynu między warstwami

- w przewodzie kołowym o stałym przekroju tory elementów są do siebie prawie równoległe

- liczba Reynoldsa Re < 2320

- rozkład prędkości jest paraboliczny

Warunki te odpowiadają warunkom równania Hagena - Poiseuille'a

22) Cechy ruchu turbulentnego :

- brak wewnętrznej spójności płynu, występują przypadkowe zaburzenia, pulsacje, sprawiające,

że ruch wewnątrz danego obszaru jest zmienny w czasie

- występuje intensywna wymiana masy i pędu między poszczególnymi warstwami będąca

wynikiem pulsacji. Płyn intensywnie się miesza

- liczba Reynoldsa Re > 2320

- przepływ jest quasi ustalony

23) Teoria Prandtla

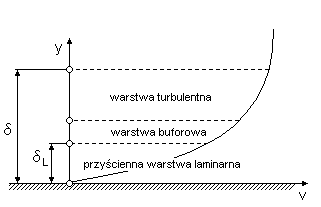
Jest to teoria określająca związek między naprężeniami a prędkością uśrednioną, przy przepływach płynów charakteryzujących się dużymi wartościami liczby Re i bazuje na teorii warstwy przyściennej.

Przyścienna warstwa laminarna występuje przy samej ściance. Jej grubość δ_L jest bardzo mała, lecz w istotny sposób oddziałuje na przepływ. Wewnątrz tej warstwy decydujący wpływ mają naprężenia lepkie τ_L.

Warstwa buforowa - w tej warstwie wpływ naprężeń turbulentnych i lepkich jest porównywalny.

Warstwa turbulentna - występują przede wszystkim naprężenia turbulentne τ_T.

Z równania pędu i popędu można wyznaczyć związek określający naprężenia styczne turbulentne

gdzie
to prędkości pulsacyjne w kierunkach OX i OY

Przy założeniach:

- droga mieszania (związana z pulsacją
) rośnie liniowo z odległością y od ścianki

- naprężenia styczne τ mają stałą wartość w przyściennej warstwie, równa naprężeniom na

ściance τ₀ (τ = τ₀ = const)

- w przyściennej warstwie laminarnej działają tylko naprężenia lepkie (τ₀ = τ_L), a w pozostałej

części warstwy przyściennej tylko naprężenia turbulentne (τ₀ = τ_T)

wyprowadzono wzór który określa rozkład prędkości w przyściennej warstwie turbulentnej

gdzie: y - odległość od ścianki,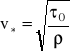
- prędkość dynamiczna,
- uśredniona prędkość w przyściennej warstwie turbulentnej,
- stała ≈ 0,4 ; C - stała wyznaczana w zależności od rodzaju powierzchni ścianki.

Wnioski: w przyściennej warstwie turbulentnej rozkład prędkości jest logarytmiczny, a w przyściennej warstwie laminarnej jest linowy.

24) Opory liniowe - omówić wykres Colebrookea- White'a. Dlaczego w strefie rur hydraulicznie gładkich λ zależy tylko od Re?

Wykres jest wykonany w logarytmicznym układzie współrzędnych i

Opis wykresu:

• Re < 2320 (ruch laminarny) na wykresie znajduje się linia prosta będąca wykresem zależności λ = 64 / Re

• 2320 < Re < 4000 - zmienny charakter ruchu, wartości λ nie są określone (obszar zakreskowany). Jest to strefa gwałtownego wzrostu współczynnika oporów liniowych, strefa ta nie jest dokładnie przebadana

• Re > 4000 można wyróżnić trzy strefy:

1) Linia najniżej położona wyznacza strefę rur hydraulicznie gładkich. W strefie tej przyścienna warstwa laminarna przykrywa nierówność ścianki (δ_L > k), k = 0 → ε = 0, przepływ turbulentny nie jest dodatkowo zaburzany przez chropowatość.

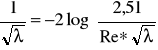
2) Obszar położony powyżej i ograniczony z prawej strony linia Re_gr nazywany jest strefą

przejściową. Przyścienna warstwa laminarna tylko częściowo pokrywa nierówności ścianki

(0 < δ_L < k), stąd współczynnik λ zalerzy od Re i od ε.

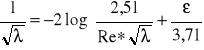
3) Obszar na prawo od linii Re_gr nazywa się strefa kwadratowej zależności oporów. Zanika

przyścienna warstwa laminarna, współczynnik λ zależy tylko od chropowatości względnej ε

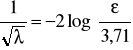
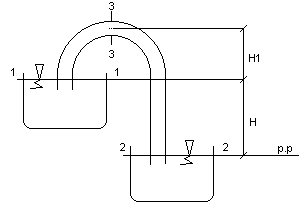
25) Lewar, wyprowadzić wzór na V i h_max

Lewar - przewód umożliwiający przepływ po między dwoma zbiornikami, którego oś wznosi się ponad swobodne zwierciadło cieczy. Warunkiem powstania ruchu w lewarze jest jego wstępne zapełnienie.

Do obliczenia prędkości średniej układamy równanie Bernoulliebo dla przekrojów 1 i 2:

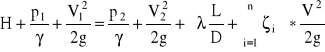
n - liczba oporów miejscowych

Dla dużych otwartych zbiorników można przyjąć p₁ = p₂ = p_a i

V₁ = V₂ ≈ 0

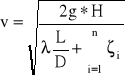
Do obliczenia maksymalnego wzniesienia lewara H₁ układamy równanie Bernoulliego dla przekrojów 1 i 3

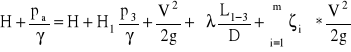
Ciśnienie cieczy p₃ musi być większe niż ciśnienie od ciśnienia wrzenia cieczy p_w w danej temperaturze strumienia. W miejsce p₃ wstawiamy p_w i z otrzymanej zależności określamy maksymalne wzniesienie H_1max przy którym wrzenie cieczy nie wystąpi.

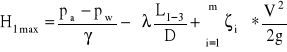
analogicznie obliczamy H_1max dla przekrojów 3 i 2, przyjmując ostatecznie mniejszą wartość.

26) Omówić sposób postępowania przy obliczaniu Q w przewodach krótkich.

Określamy kierunek przepływu w przewodzie, zakładamy przekroje oraz poziom porównawczy. Następnie układamy równanie Bernoulliego. Przekształcamy je tak aby otrzymać funkcję na Q, iteracyjnie szukamy takiego Q, które spełniałoby równość dla wyliczonej drugiej strony równania (szacowanie z wykresu, min. 3 punkty różne od zera, szukany punkt musi znajdować się między nimi).

27) Założenia i wyprowadzenia wzoru wodociągowego

Długość przewodów jest daleko większa od średnicy, niewielka ilość oporów miejscowych przez co straty miejscowe w porównaniu z liniowymi są małe i pomijane, lub uwzględniane w postaci mnożnika (1,05 - 1,1) strat liniowych. Także wysokości prędkości w równaniu Bernoulliego są pomijane i przyjmuje ono postać:

gdzie h_i jest naporem w i-tym przekroju strumienia

Podstawiając wydatek cieczy, stratę na długości przewodu h_L można zapisać w postaci

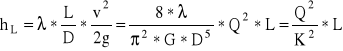
gdzie k - przepuszczalność przewodu (modul przepływu)

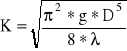
Opornością przewodu nazywa się wyrażenie
, więc wysokości strat ciśnienia można zapisać następująco

28) Podać warunki równania i naszkicować graficzne rozwiązanie przewodów połączonych równolegle i szeregowo.

Połączenie szeregowe

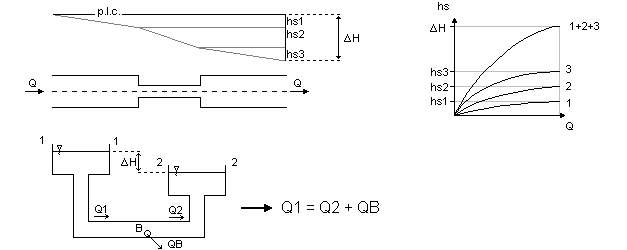
Warunki: Q₁ = Q₂ = ... = Q_n = const , ΔH = hs₁ + hs₂ + ... + hs_n

Dla znanej różnicy naporów Δh rozwiązanie sprowadza się do wyznaczenia z równania strat niewiadomej Q.

Rozwiązanie graficzne: sumując charakterystyki przewodów przez dodanie rzędnych ΔH_i przy jednakowych odciętych (wydatkach), otrzymujemy wypadkową charakterystykę połączenia szeregowego (1 + 2 + 3). Dla zadanej wartości ΔH możemy wyznaczyć szukany wydatek Q.

Połączenie równoległe

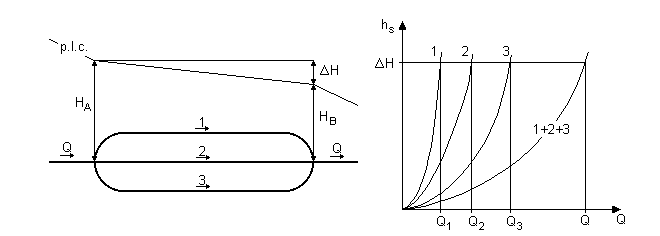
Warunki: Q₁ + Q₂ + ... + Q_n = Qconst , H_A - H_B = ΔH = hs₁ = hs₂ = ... = hs_n

Wypadkowa charakterystykę przewodów otrzymujemy przez dodanie odciętych Q_i przy stałych wysokościach strat ciśnienia. Dla znanego sumarycznego wydatku Q możemy wyznaczyć różnicę naporów ΔH oraz wydatki w poszczególnych przewodach.

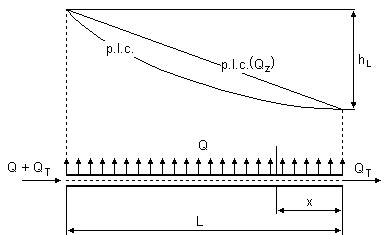
29) Wzór dla przewodu równomiernie wydatkowanego

Założenia: straty lokalne w przewodzie o stałej średnicy D są pomijalnie małe oraz ruch odbywa się w strefie kwadratowej λ(ε) → K = const

Q_z - wydatek zastępczy, który powoduje takie same straty ciśnienia jak rzeczywisty, stale malejący przepływ.

Łączna wysokość strat ciśnienia na długości L wynosi

gdzie Q_T - wydatek tranzytowy.

Najczęściej przyjmuje się, że wydatek zastępczy

Q_z = Q_T + 0,55Q

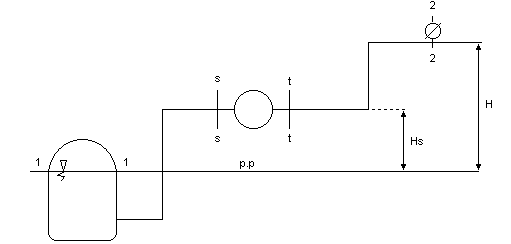
30) Maksymalna wysokość ssania i podnoszenia pompy oraz charakterystyki.

Wysokość energii jaką ma dostarczyć pompa przepływającej cieczy jest nazywana całkowita wysokością podnoszenia pompy - H₀. Wyznaczamy ją z równania Bernoullieg dla przekrojów 1 i 2 założonych po obu stronach pompy

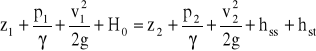
Po przekształceniu (v₁ = 0, H = z₂ - z₁ - geometryczna wysokość podnoszenia pompy) otrzymuje się

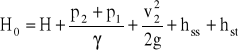
Wysokością ssania pompy H_s nazywa się wysokość wzniesienia osi pompy ponad swobodne zwierciadło cieczy w zbiorniku zasilającym.

Układając równanie Bernoulliego dla przekrojów 1 i s, można wyznaczyć zależność wysokości ssania od parametrów przepływu w przewodzie ssawnym pompy.

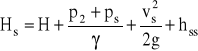
Ciśnienie p_s musi być większe od ciśnienia pary nasyconej p_w (ciśnienie wrzenia cieczy)

Podstawiając do powyższej zależności ciśnienie wrzenia p_w, otrzymuje się

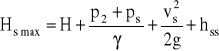
Podstawowe charakterystyki pracy pompy wirnikowej

Funkcje: H_p(Q); N_s(Q) i η(Q) dotyczą stałej prędkości kątowej pompy. H_p(Q) - charakterystyka pompy. Optymalny zakres pracy pompy mieści się w okolicy maksymalnej sprawności (obszar zakreskowany na rysunku).

31) Punkt pracy

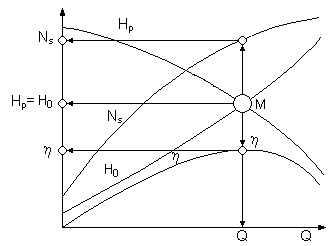
Punkt pracy jest to punkt (M) przecięcia się charakterystyki pompy H_p(Q) i sprawdzonej charakterystyki przewodu H₀(Q). Określa on rzeczywiste wartości natężenia przepływu Q i wysokości podnoszenia pompy H_p. Znajomość punktu pracy pozwala wyznaczyć szukane wartości mocy N oraz sprawności η.

32) Układ trzech zbiorników, graficzne rozwiązanie

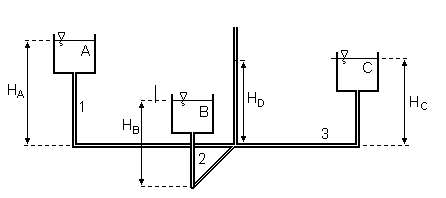
Założenia:

H_A > H_B > H_C to zbiornik A zawsze jest zbiornikiem zasilającym (H_A > H_D), a zbiornik C zasilanym (H_C < H_D)

Zbiornik B może być:

- zasilający (H_B > H_D) → Q₁ + Q₂ = Q₃

- nieczynny (H_B = H_D) → Q₂ = 0; Q₁ = Q₃

- zasilany (H_B < H_D) → Q₁ = Q₂ + Q₃

Zakładając, że H_B > H_D można ułożyć następujący układ równań:

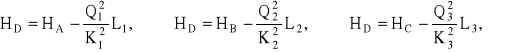
Rozwiązując ten układ można wyznaczyć szukane wartości Q₁, Q₂, Q₃ oraz H_D. Jeżeli obliczona wysokość H_D będzie mniejsza od naporu H_B to warunki będą spełnione. W przeciwnym wypadku należy przyjąć inny wariant przepływu.

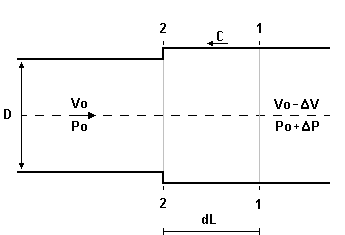
33) Wyprowadzić wzór Żukowskiego na przyrost ciśnienia w uderzeniu hydraulicznym.

Zmiany gęstości i pola przekroju poprzecznego są na tyle małe w porównaniu ze zmianami prędkości i ciśnienia iż można je pominąć.

Rozpatrujemy odcinek przewodu o długości dL i średnicy D. Fala ciśnienia w chwili t znajduje sie w przekroju 1 i po czasie dt dociera do przekroju 2 ( c =dL/dt, c - prędkość fali). W czasie dt warunki jakie panowały na prawo od przekroju 1 ustaliły się na odcinku dL przewodu i wynoszą:

v = v₀ - Δv ; p = p₀ + Δp ; ρ = ρ₀ + ρΔ ; A = A₀ + ΔA, na lewo od przekroju 2 warunki nie uległy zmianie i wynoszą v₀, p₀, ρ₀, A_0. Stosując równanie ruchu (pędu i popędu) do cieczy zawartej między przekrojami 1 i 2 można zapisać:

przyjmując, że A₀ = A i wstawiając za dL dt *c otrzymujemy :

Δp = ρ * ΔV * c

Gdy prędkość spada to rośnie ciśnienie, maksymalne ciśnienie występuje gdy prędkość spadnie do zera.

34) Omówić metody przeciwdziałania uderzeniu hydraulicznemu i uzasadnić

Uderzeniem hydraulicznym są nazywane gwałtowne zmiany ciśnienia w przewodzie pod ciśnieniem, spowodowane szybkimi w czasie zmianami prędkości przepływu cieczy.

Metody przeciwdziałania:

- stosowanie długiego czasu otwierania i zamykania zaworu (ograniczona zmiana ciśnienia Δp)

- stosowanie zaworów bezpieczeństwa i zbiorników powietrznych (zbiornik powietrzny przejmuje

część z przewodu z chwilą wzrostu ciśnienia, przeciwdziała to szybkiemu spadkowi prędkości;

działanie zaworu bezpieczeństwa następuje z chwilą przekroczenia ciśnienia p powyżej pewnej

ustalonej wartości dopuszczalnej)

- montowanie przewodów odkształcalnych

- ustawianie małych prędkości cieczy w przewodach (małe zmiany ciśnienia)

- wtłaczanie powietrza atmosferycznego do strumienia cieczy z chwila spadku ciśnienia (podnosi

ciśnienie w przewodzie powyżej wartości ciśnienia wrzenia cieczy w danej temperaturze)

35) Wzór Stokesa na parcie, wyznaczyć związek parcia na ciało opływane.

Parcie na ciało opływane jest funkcją zależną od:

l - charakterystyczny wymiar liniowy

k - chropowatość powierzchni ciała

v - prędkość przepływu strumienia

ρ - gęstość płynu

μ - lepkość płynu

Czyli P = P (l, k, v, μ, ρ), parcie to zapisuje się w postaci
, gdzie c_x - współczynnik oporu, A_x - powierzchnia przekroju czołowego opływanego ciała. Współczynnik oporu c_x jest funkcją liczby Reynoldsa Re oraz chropowatości względnej ε.

Opływ może mieć charakter laminarny lub turbulentny.

Przy opływie laminarnym chropowatość powierzchni k nie ma wpływu na opory. Siła parcia w ruchu laminarnym jest proporcjonalna do prędkości , c_x jest odwrotnie proporcjonalne do prędkości v, czyli posiada formę c/Re. Stąd

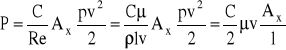
stała C zależy od kształtu opływanego ciała.

Na przykład dla kuli opływanej ruchem laminarnym (C = 24), przyjmując za l średnicę kuli, l = d, otrzymuje się wzór Stokesa

Przy przepływach turbulentnych zagadnienie jest bardziej złożone. W wielu przypadkach tego ruchu elementem decydującym o zaburzeniach przepływu jest sam kształt. c_x zależy wyłącznie od kształtu i położenia ciała względem kierunku napływu strumienia i od liczby Reynoldsa Re.

Dla przepływu o rozwiniętej turbulencji opory ruchu są proporcjonalne do v². W tym przypadku zanika wpływ liczby Re i współczynnik c_x przyjmuje wartość stałą.

36) Koryta - wyprowadzić wzór Chēzy'ego

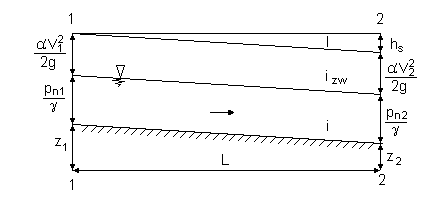
Zakładamy, że w korycie występuje ruch jednostajny. Aby warunek ten był spełniony koryto musi mieć stały przekrój poprzeczny o niezmiennej na długości szorstkości ścian i dna i stałym spadku dna i. Przepływ jednostajny jest ruchem ustalonym, stąd prędkość oraz energia kinetyczna cieczy są stałe. Oznacza to, że spadek dna równy jest spadkowi linii zwierciadła (piezometrycznej linii ciśnień) i_zw, jak i spadkowi linii energii (spadkowi hydraulicznemu) I i = i_zw = I

Układając równanie Bernoulliego dla przekrojów 1 i 2 koryta, można zapisać

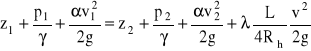
gdzie: R_h - promień hydrauliczny strumienia w korycie (R_h = A / U),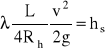
.

Ponieważ p₁ = p₂ = p, v₁ = v₂ = v, z₁ - z₂ = iL = IL więc

Wprowadzając oznaczenie
, otrzymujemy wzór na średnią prędkość w poprzecznym przekroju koryta

37) Ruch krytyczny w korycie otwartym.

W korycie otwartym linia energii jest wzniesiona ponad linię zwierciadła cieczy o wartość
. Przy oznaczeniu głębokości napełnienia przez h, wysokość energii mechanicznej strumienia względem dna kanału wynosi

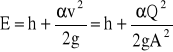
gzie pole przekroju poprzecznego koryta A jest funkcją napełnienia A = A(h). Przy założeniu stałego wydatku Q = const, całkowita energia w danym przekroju zmienia się w funkcji napełnienia kanału:

h → 0 : A(h) → 0, E → ∞

h → ∞ : A(h) → ∞, E → ∞

Dla obu przypadków energia strumienia E wzrasta do nieskończoności. Istnieje więc taka głębokość, dla której energia ma wartość minimalną. Głębokość taka nazywa się krytyczną a odpowiadający jej ruch ruchem krytycznym.

Kryterium ruchu krytycznego dla Q = const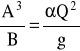
,

B - szerokość koryta

Przyjmując głębokość średnią h_śr (h_śr = A / B) za charakterystyczny wymiar liniowy l koryta możemy zapisać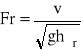
, dla α ≈ 1 wynika, że ruch krytyczny występuje gdy liczba Froude'a jest równa jedności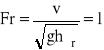
.

Warunek tan jest spełniony, jeżeli:

- przy określonym Q = const całkowita energia strumienia E jest minimalna,

- przy zadanej energii E = const natężenie przepływu Q jest maksymalne.

Wszystkie parametry ruchu krytycznego: prędkość, głębokość, spadek dna, noszą nazwę parametrów krytycznych.

Głębokość krytyczną wyznacza się dla określonego kształtu przekroju poprzecznego koryta na przykład dla przekroju prostokątnego

(A = h_krB)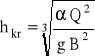
.

Ruch krytyczny (Fr = 1) nie występuje samoistnie w naturze, stanowi on natomiast granicę między obszarami ruchu rwącego i spokojnego.

Jeżeli:

- h < h_kr to w korycie występuje ruch rwący (podkrytyczny) Fr > 1

- h > h_kr to w korycie występuje ruch spokojny (nadkrytyczny) Fr < 1

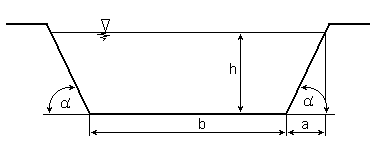
38) Warunek na koryto hydraulicznie najkorzystniejsze

Najkorzystniejszym pod względem hydraulicznym jest taki przekrój koryta , który przy danym polu przekroju A, szorstkości n oraz spadku dna i zapewnia największy wydatek Q cieczy w ruchu jednostajnym. Dla przyjętych warunków największy wydatek Q zapewnia koryto o najmniejszym obwodzie zwilżonym U. Najmniejszy obwód zwilżony ma przekrój półkolisty. W praktyce przekrój ten jest rzadko stosowany ze względów wykonawczych.

Najczęściej spotykane są koryta o przekroju trapezowym.

Warunek na hydraulicznie najkorzystniejszy przekrój trapezowy koryta otwartego

,

gdzie m - współczynnik nachylenia skarp m = a/h.

Najkorzystniejszy kąt nachylenia skarp α koryta trapezowego wynosi α = 60⁰.

39) Sposób na obliczanie kanalizacji grawitacyjnej.

Grawitacyjny ruch jednostajny odbywa się przy niecałkowitym napełnieniu przekroju poprzecznego koryta. Z tego względu przepływ w przewodach bezciśnieniowej kanalizacji jest obliczany jak w korytach otwartych.

Średnia prędkość w przekroju poprzecznym
,

gdzie β - współczynnik sprawności przekroju, równy ilorazowi prędkości w kanale przy częściowym (h) i całkowitym (H) napełnieniu: β = v(h)/v₀(H); W₀ - charakterystyka prędkości, równa średniej prędkości przepływu cieczy przy całkowitym napełnieniu przewodu i spadku dna równym jedności [m/s].

Objętościowe natężenie przepływu

gdzie α - współczynnik sprawności przekroju, równy ilorazowi wydatku w kanale przy częściowym (h) i całkowitym (H) napełnieniu kanału, α = Q(h)/Q₀(H); K - przepuszczalność przewodu dla przepływu cieczy przy całkowitym napełnieniu przewodu i spadku dna równym jedności [m³/s].

Współczynniki sprawności α, β odczytuje się z krzywych sprawności przekroju w funkcji h/H, dla określonego kształtu przewodu kanalizacyjnego. Wartości charakterystyki W₀ i przepuszczalności K₀ zależą od charakterystycznych wymiarów (H, B) określonego kształtu kanału oraz od szorstkości n.

Obliczenia natężenia i prędkości przepływu w przewodzie o danym kształcie i znanych wartościach B i H lub (D) sprowadza się do :

- przyjęcia z tabeli wartości K₀ oraz W₀,

- odczytania z krzywej sprawności wartości α i β dla znanego napełnienia h/H,

- obliczenia natężenia oraz prędkości

40) Omówić funkcję odskoku + wykres.

Odskok hydrauliczny występuje przy przejściu ruchu rwącego w spokojny. Jest to zjawisko gwałtownego zwiększenia się głębokości strumienia od h₁ < h_kr do h₂ > h_kr. Zaburzenia wywołane odskokiem pochłaniają znaczną część energii strumienia.

Funkcja odskoku θ(h)

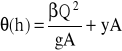
gdzie: β - współczynnik pędu związany z nierównomiernym rozkładem prędkości w przekroju poprzecznym strumienia, yA - moment statyczny pola A względem zwierciadła cieczy, y - zagłębienie środka ciężkości, Q - wydatek

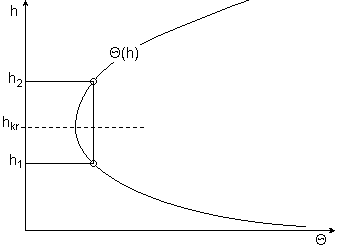
Funkcja jest ciągła i przyjmuje odatnie wartości z całym zakresie zmienności h.

Dla h → 0 oraz, h → ∞ funkcja θ(h) dąży do nieskończoności. W ruchu turbulentnym funkcja odskoku θ(h) podobnie jak całkowita energia E(h), osiąga w danym przekroju koryta minimum przy krytycznej wartości napełnienia.

41) Wyprowadzić wzór na czas opróżnienia zbiornika, wypływ przez otwór duży .

Otwarty zbiornik o zmienny polu przekroju i początkowym napełnieniu H jest opróżniany przez otwór o polu przekroju A₀ i współczynniku wydatku μ. W pewnej chwili zwierciadło cieczy będzie wzniesione na wysokość z ponad otworem, a powierzchnia zwierciadła będzie równa A_z. Po czasie dt zwierciadło cieczy obniży się o dz.

Można przyjąć, że w tym czasie wydatek Q nie ulegnie zmianie i będzie wynosił

.

Porównując objętość cieczy jaka przepłynie przez otwór w czasie dt z objętością o jaką zmniejszy się zawartość naczynia można zapisać

.

Przekształcając to równanie ze względu na dt i podstawiając zależność na Q, otrzymujemy

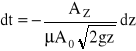
Czas obniżenia się swobodnego zwierciadła cieczy do pewnej wysokości z_k wynosi

.

We wzorze należy określić zależność A_z = A_z(z), współczynnik wydatku μ jest średnią z wartości

μ określaną dla z = H i z = z_k.

42) Wypływ przez otwór duży

Rys. 10.5 strona 234

W niezatopionym otworze dużym należy uwzględnić różne prędkości które narastają wraz z zagłębieniem punktu otworu pod swobodnym zwierciadłem cieczy. Otwór umieszczony w ściance zbiornika, nachylonej do poziomu pod kątem α, ma kształt pokazany na kładzie. Do obliczenia wydatku Q należy podzielić otwór ten na elementarne paski poziome o wysokości dz. Każdy z tych pasków jest otworem małym o powierzchni dA = y dz / sin α. Szerokość otworu y jest funkcją zagłębienia: y = y(z). Jeżeli pominie się energię prędkości opadania cieczy w zbiorniku (v₁ ≈ 1), prędkość wypływu cieczy ze szczeliny, zagłębionej o z pod swobodnym zwierciadłem, w zbiorniku wyniesie

Elementarny wydatek dQ jest równy v₂dA. Całkowity wydatek Q jest sumą wydatków elementarnych i wynosi

.

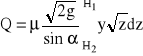
Współczynnik wydatku μ charakteryzuje pracę całego otworu. Współczynnik ten jest zmienny podobnie jak przy otworach małych. Jego orientacyjna wartość wynosi 0,6.

43) Dlaczego otwór zatopiony pracuje jak otwór mały?

Otwór jest traktowany jako mały, jeżeli różnica prędkości w najwyższym i najniższym punkcie otworu jest mała w stosunku do prędkości średniej, w przeciwnym wypadku otwór jest traktowany jako duży. Przy tym podziale nie maja znaczenia wymiary otworu, lecz wartość stosunku wysokości otworu h do wysokości zagłębienia środka ciężkości otworu poniżej swobodnego zwierciadła cieczy w zbiorniku z_s. W praktyce inżynierskiej, otwór może być traktowany jako mały, jeżeli iloraz h/z_s jest mniejszy od 0,1.

Otwór zatopiony pracuje jak otwór mały, ponieważ prędkość wypływu cieczy przez otwór zależy wyłącznie od różnicy poziomów zwierciadeł cieczy i jest praktycznie taka sama w każdym punkcie otworu.

44) Wyprowadzić wzór na przelew Tompsona

Przelewem nazywa się ściankę przegradzającą koryto, bądź przewód o swobodnym zwierciadle cieczy, gdy ciecz po spiętrzeniu przelewa się przez tą przeszkodę.

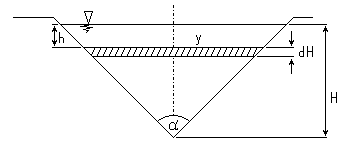
Przelew Tompsona jest to przelew o ostrych krawędziach i kącie wierzchołkowym

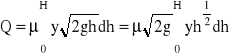
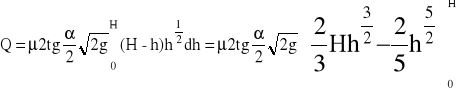
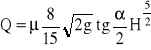
Dla α = 90⁰ i μ= 0,59, wzór przyjmuje postać

45) Wyjaśnić paradoks Saint - Venanta - Wantzela.

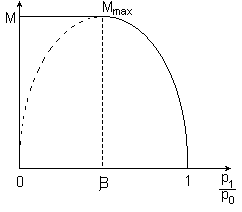
Wykres przedstawia zależności masowego natężenia wypływu M w funkcji ilorazu ciśnień P₁/P₀, dla stałych parametrów gazu w zbiorniku. Ze spadkiem ciśnienia p₁, wielkość M początkowo rośnie, a po osiągnięciu wartości maksymalnej M_max, dla p₁/p₀ = β, ponownie maleje do zera. Badania doświadczalne wskazują, że dla p₁/p₀ < β masowe natężenie przepływu nie zmienia się i jest równe wartości maksymalnej.

Przedstawiona rozbieżność jest nazywana „paradoksem Saint - Venanta - Wantzela.

46) Jak działa kryza krytyczna?

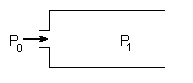
Kryza krytyczna jest to tak dobrany wlot do przewodu, że wewnątrz przewodu utrzymuje się stałe natężenie masowe P₁/P₀ < β stąd

M = M_max = const.

47) Wykazać, że λ jest stałe, a prędkość rośnie.

Dla gazu:

Mimo, że prędkość na długości przewodu rośnie, to Re = const → λ = const.

48) Gazociągi niskiego ciśnienia.

W gazociągach niskiego ciśnienia zmiany ściśliwości z są nieistotne, stąd wzór na masowe natężenie przepływu dla przewodu kołowego przyjmuje postać

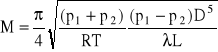
Gęstość gazu dla średniego ciśnienia z początkowego i końcowego przekroju wynosi

po przekształceniu otrzymuje się

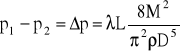
Wykorzystując równanie ciągłości, można sprowadzić powyższą zależność do postaci wzoru Darcy'ego - Weisbacha

Współczynnik oporów liniowych λ(Re, ε) wyznacza się jak dla płynów nieściśliwych, W gazociągach niskiego ciśnienia odbywa się przeważnie ruchem laminarnym.

49) Pojęcie ciśnienia czynnego i sposób wyznaczania.

Krążenie wody w instalacjach zapewnia tzw. ciśnienie czynne.

Dla ogrzewań pompowych, w których wykorzystuje się pracę pompy obiegowej (cyrkulacyjnej), ciśnienie czynne stanowi sumę ciśnienia grawitacyjnego Δp_g oraz ciśnienia pompowego Δ p_p (odpowiadającego wysokości podnoszenia pompy H_p).

Δp_cz = Δp_p + Δp_g

Dla ogrzewań grawitacyjnych (bez pompy obiegowej) ciśnienie czynne jest równe ciśnieniu grawitacyjnemu. W przybliżeniu równe:

Δp_g ≈ H(γ_p - γ_z)

gdzie: H - różnica wysokość położenia środków ciężkości grzejnika i źródła ciepła

(γ_p - γ_z) - różnica ciężarów właściwych wody w części powrotnej i zasilającej.

50) Studnie. Wzór na studnie zwykłe, omówić metody wyznaczania współczynnika filtracji.

Współczynnik filtracji (przesączalności) jest to wielkość zależna od rodzaju gruntu i rodzaju płynu. K = K_p*g / ν, gdzie K_p - współczynnik przepuszczalności, ν - lepkość kinematyczna płynu.

Współczynnik filtracji wyznacza się trzema metodami:

a) Obliczeniowa

b) Laboratoryjną

c) Próbnego pompowania (terenową)

Wzór na studnie zwykłe

,

gdzie H₀ - h₀ = s₀ - określa depresję wody w studni, r₀ - promień dopływu wody do studni, R - zasięg (promień) depresji, określany z empirycznego wzoru Sichardta

.

Dla znanych wartości Q, r, z możliwy jest określenie ze wzoru

,

współczynnika filtracji k dla warstwy wodonośnej. Pomiaru wysokości z dokonuje się w odwiercie (tzw. studni kontrolnej) oddalonym o r (r < R) od osi studni). Jest to metoda polowa określania współczynnika filtracji k.

51) Pomiar prędkości - zasada działania rurki spiętrzającej (szkic rurki) wzór na prędkość.

Rurka spiętrzająca jest najprostszym anemometrem (przyrządem do pomiaru ciśnienia). Do pomiaru prędkości lokalnej stosuje się najczęściej rurkę Prandtla, w której ciśnienie statyczne jest mierzone na obwodzie walcowej powierzchni bocznej rurki.

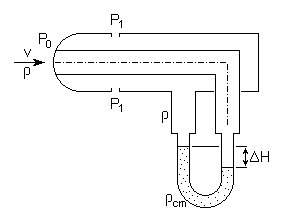
Prędkość wyznacza się ze wzoru:

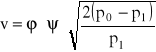
, gdzie:

φ - współczynnik prędkości, ψ - współczynnik uwzględniający wpływ ściśliwości gazu.

52) Na czym polega zjawisko Venturiego. Wyprowadź wzór n Q dla zwężki Venturiego.

Zasada działania zwężki Venturiego polega na pomiarze różnicy energii potencjalnej wywołanej zmianą energii kinetycznej (wskutek przewężenia strumienia) oraz oporami ruchu.

Obierając dwa przekroje 1 i 2 przewodu poziomego, z równania Bernoulliego dla cieczy doskonałej otrzymuje się

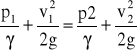
Z równania ciągłości, dla ρ = const, wynika

gdzie m - moduł zwężki (m = A₂/A₁).

Po podstawieniu do równania Bernoulliego i przekształceniu otrzymuje się wzór na prędkość średnią w przewodzie

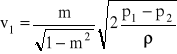
Masowe natężenie przepływu cieczy doskonałej wynosi

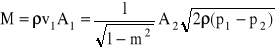
Dla cieczy rzeczywistej trzeba uwzględnić wpływ oporów ruchu między przekrojami 1 i 2 zwężki.

Wpływ ten można uwzględnić przez współczynnik poprawkowy k (k = 0,96 - 1)

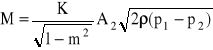
Wprowadzając pojęcie liczby przepływów

masowe natężenie przepływu cieczy rzeczywistej jest równe

a objętościowe (wydatek)

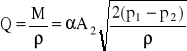
15

---