POLITECHNIKA RADOMSKA im. Kazimierza Pułaskiego WYDZIAŁ TRANSPORTU		LABORATORIUM MIERNICTWA		Data:
Wykonali:		Grupa:	Zespół:	Rok akademicki:
Temat:	Pomiary kompensacyjne		Nr ćwiczenia:	Ocena:

1. Cel ćwiczenia:

Celem ćwiczenia jest poznanie działania kompensatora napięcia stałego oraz jego zastosowanie do pomiarów siły elektromotorycznej, napięcia, natężenia prądu, rezystancji a także wyznaczenie błędów występujących w pomiarach kompensacyjnych oraz analiza wpływu dokładności użytych do jego budowy elementów.

2. Układ pomiarowy:

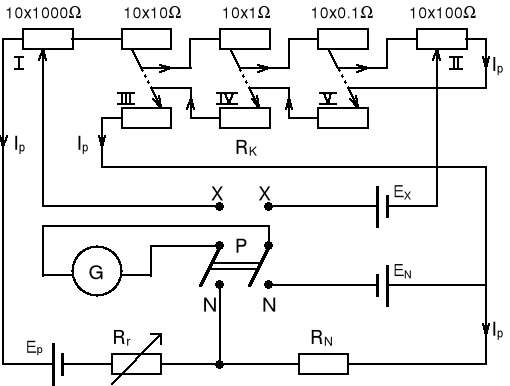
Rys. 1. Schemat układu do pomiaru SEM E_X za pomocą kompensatora Feussnera

3. Tabele pomiarowe:

Tabela 1. - Pomiar napięcia za pomocą kompensatora

Lp.	RK	Ex	ΔRK	ΔEx	α		δSg	δn	δ	Ex ±Δ Ex
	[Ω]	[V]	[Ω]	[V]	[dz]	[V]	[%]	[%]	[%]	[V]
1	7820.6	0.78206	0.1	0.0015	1	0.78263	0.21109	2.557E-2	0.23666	0.782	±	0.00185
2	7823.6	0.78236	0.1	0.0015	1	0.78263	0.21103	2.556E-2	0.23659	0.782	±	0.00185
3	7824.4	0.78244	0.1	0.0015	1	0.78263	0.21102	2.556E-2	0.23658	0.782	±	0.00185
4	7824.6	0.78246	0.1	0.0015	1	0.78263	0.21101	2.556E-2	0.23657	0.782	±	0.00185
5	7824.9	0.78249	0.1	0.0015	1	0.78263	0.21101	2.556E-2	0.23657	0.782	±	0.00185
6	7825.2	0.78252	0.1	0.0015	1	0.78263	0.21100	2.556E-2	0.23656	0.783	±	0.00185
7	7825.3	0.78253	0.1	0.0015	1	0.78263	0.21100	2.556E-2	0.23656	0.783	±	0.00185
8	7826.8	0.78268	0.1	0.0015	1	0.78263	0.21097	2.556E-2	0.23653	0.783	±	0.00185
9	7827.8	0.78278	0.1	0.0015	1	0.78263	0.21096	2.555E-2	0.23651	0.783	±	0.00185
10	7828.3	0.78283	0.1	0.0015	1	0.78263	0.21095	2.555E-2	0.23649	0.783	±	0.00185
11	7828.4	0.78284	0.1	0.0015	1	0.78263	0.21094	2.555E-2	0.23649	0.783	±	0.00185
12	7828.7	0.78287	0.1	0.0015	1	0.78263	0.21094	2.555E-2	0.23649	0.783	±	0.00185
13	7828.7	0.78287	0.1	0.0015	1	0.78263	0.21094	2.555E-2	0.23649	0.783	±	0.00185
14	7828.5	0.78285	0.1	0.0015	1	0.78263	0.21094	2.555E-2	0.23649	0.783	±	0.00185
15	7829.0	0.7829	0.1	0.0015	1	0.78263	0.21093	2.555E-2	0.23648	0.783	±	0.00185

Przykładowe obliczenia:

[V]

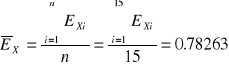
[V]

[%]

[%]

[%]

[%]

[%]

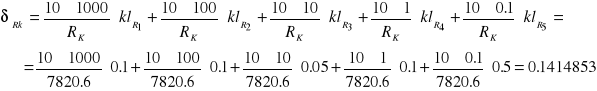
[V]

Wynik pomiaru:
[V]

Tabela 2. - Tabela pomocnicza dla metody Gaussa

Lp.	RK	Ex		ΔEx	σr	ΔEx>3σr	σEx	Ex±3σEx
	[Ω]	[V]	[V]	[V]			[V]	[V]
1	7820.6	0.78206	0.782632	5.7197E-4	2.464E-4	-	6.362E-5	0.78206	±	1.909E-4	8.135E-5
2	7823.6	0.78236	0.782632	2.7197E-4	2.464E-4	-	6.362E-5	0.78236	±	1.909E-4	8.1319E-5
3	7824.4	0.78244	0.782632	1.9199E-4	2.464E-4	-	6.362E-5	0.78244	±	1.909E-4	8.1311E-5
4	7824.6	0.78246	0.782632	1.7202E-4	2.464E-4	-	6.362E-5	0.78246	±	1.909E-4	8.1309E-5
5	7824.9	0.78249	0.782632	1.4198E-4	2.464E-4	-	6.362E-5	0.78249	±	1.909E-4	8.1305E-5
6	7825.2	0.78252	0.782632	1.12E-4	2.464E-4	-	6.362E-5	0.78252	±	1.909E-4	8.1302E-5
7	7825.3	0.78253	0.782632	1.0199E-4	2.464E-4	-	6.362E-5	0.78253	±	1.909E-4	8.1301E-5
8	7826.8	0.78268	0.782632	4.7982E-5	2.464E-4	-	6.362E-5	0.78268	±	1.909E-4	8.1286E-5
9	7827.8	0.78278	0.782632	1.48E-4	2.464E-4	-	6.362E-5	0.78278	±	1.909E-4	8.1275E-5
10	7828.3	0.78283	0.782632	1.9801E-4	2.464E-4	-	6.362E-5	0.78283	±	1.909E-4	8.127E-5
11	7828.4	0.78284	0.782632	2.0802E-4	2.464E-4	-	6.362E-5	0.78284	±	1.909E-4	8.1269E-5
12	7828.7	0.78287	0.782632	2.38E-4	2.464E-4	-	6.362E-5	0.78287	±	1.909E-4	8.1266E-5
13	7828.7	0.78287	0.782632	2.38E-4	2.464E-4	-	6.362E-5	0.78287	±	1.909E-4	8.1266E-5
14	7828.5	0.78285	0.782632	2.1803E-4	2.464E-4	-	6.362E-5	0.78285	±	1.909E-4	8.1268E-5
15	7829	0.7829	0.782632	2.6799E-4	2.464E-4	-	6.362E-5	0.7829	±	1.909E-4	8.1263E-5

Przykładowe obliczenia:

[V]

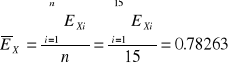
[V]

[V]

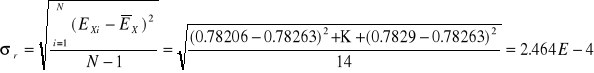
[V]

[V]

[V]

Wynik pomiaru w oparciu o metodę Gaussa

(3-sigmowa wartość niepewności):

[V]

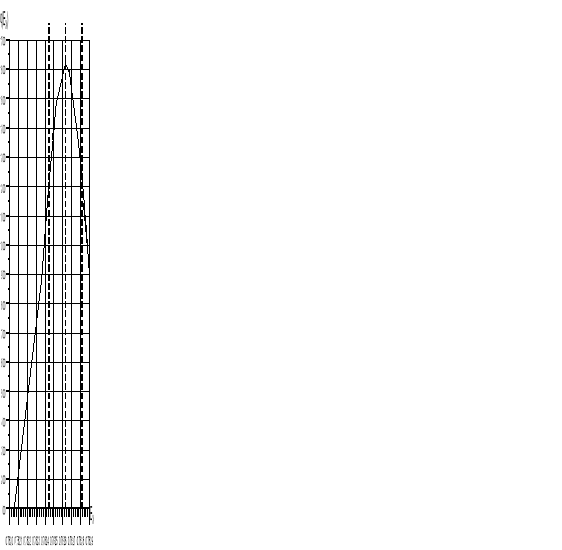
Wykres funkcji rozkładu normalnego Gaussa

mierzonnego napięcia E_X

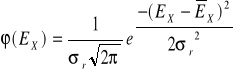
EX	0.78206	0.78236	0.78244	0.78246	0.78249	0.78252	0.78253	0.782632	0.78268	0.78278	0.78283	0.78284	0.78287	0.78287	0.78285	0.7829
σr	2.464E-4
ϕ(EX)	109	880	1195	1269	1371	1460	1486	1619	1588	1351	1172	1133	1015	1015	1094	896

Wnioski:

Naszym zadaniem było wykonanie pomiaru napięcia za pomocą kompensatora. Nasz pomiar był obarczony błędami wynikającymi z dokładności wykonania użytych przez nas elementów. Największy wpływ na wielkość błędu miały klasy rezystorów dekadowych R_K. Mniejszy, ale także istotny, miały klasy rezystora wzorcowego R_N, wzorcowego ogniwa Westona E_N oraz błąd nieczułości związany z wykonaniem galwanometru. O wysokiej dokładności pomiarów wykonywanych za pomocą kompensatora może świadczyć całokwity błąd względny δ=0.24.

Na podstawie wyników pomiarów wyznaczyliśmy także rozkład Gaussa mierzonego napięcia E_X. Interpretacja fizyczna wykresu tego rozkładu jest taka: pole zawarte pod krzywą wykresu Gaussa w odpowiednim zakresie parametru E_X określa prawdopodobieństwo znalezienia się wartości mierzonej E_X w tym przedziale. Oznacza to, że prawdopodobieństwo wystąpoienia dużych błędów jest małe, ponieważ pole pod krzywą dla wartości E_X dużo różniących się od
jest małe. Największe zaś jest prawdopodobieńswo wystąpienia wyników bardzo zbliżonych do
. Na wykresie liniami przerywanymi zaznaczyliśmy
,
oraz
, czyli przedział wyników dla 3-sigmowej wartości niepewności. Jak widać z wykresu, nie wszyskie nasze pomiary zawierały się w tym przedziale.

Porównując błędy opracowane metodą konwencionalną oraz Gaussa zauważamy, że w tej drugiej metodzie błąd jest mniejszy o rząd wielkości. Wynika to z faktu, że w metodzie Gaussa nie bierzemy pod uwagę dokładności wykonania przyrządów użytych do pomiarów, a skupiamy się na analizie pewności uzyskanych wyników.

1

---