1. Wstęp Teoretyczny

Pompa jest to urządzenie mechaniczne służące do wymuszania przepływu cieczy i zwiększające energię mechaniczną przepływającego strumienia. Instalacja pompowa składa się z przewodu ssawnego, zespołu pompowego i przewodu tłocznego. Dla każdej pompy umieszczonej na przewodzie określa się trzy charakterystyczne wysokości, zwane wysokościami manometrycznymi:

• wysokość ssania (różnica rzędnych osi pompy i linii energii tuż przed pompą),

• wysokość tłoczenia (różnica rzędnych osi pompy i linii energii tuż za pompą),

• wysokość podnoszenia pompy (różnica rzędnych linii energii przed i za pompą).

Wysokość podnoszenia pompy jest wartością zmienną i zależy od natężenia przepływu. W przypadku braku przepływu (zamknięty zawór na przewodzie tłocznym) także jest wytwarzana różnica ciśnień. Wysokość podnoszenia pompy obliczamy ze wzoru:

gdzie:

H_p - wysokość podnoszenia,
H_t - wysokość tłoczenia,
H_s - wysokość ssania,
Δz - różnica rzędnych obydwu przekroi pomiarowych.

Wysokość tłoczenia i wysokość ssania obliczamy odpowiednio ze wzorów

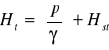
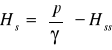
gdzie:

H_t - wysokość tłoczenia,

H_s - wysokość ssania,

H_st - straty w przewodzie tłocznym,

H_ss - starty w przewodzie ssawnym,

p - ciśnienie w manometrze,

a - wysokość zamocowania manometrów na przewodzie,

γ - ciężar właściwy wody.

Pracująca pompa przekazuje strumieniowi cieczy pewną energię. Jej wartość podzielona przez czas daje nam moc użyteczną, czyli moc przekazaną strumieniowi. Aby ją obliczyć korzystamy ze wzoru

gdzie:

N_u - moc użyteczna pompy,

γ_H2O - ciężar właściwy wody,

Q - objętościowe natężenie przepływu,

H_p - wysokość podnoszenia pompy.

Moc pobieraną przez pompę oznaczamy przez N_p. Ze względu na opory tarcia i opory hydrauliczne jest ona większa od mocy przekazywanej strumieniowi N_u. Stosunek obu tych mocy jest miarą jakości urządzenia i nosi nazwę współczynnika sprawności pompy oznaczanego przez η.

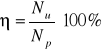
Charakterystyki pompy przedstawia się za pomocą wykresów zależności trzech charakterystycznych wysokości pompy (H_p, N_u, η) umieszczonych na osi rzędnych o potrójnej skali od natężenia przepływu Q umieszczonej na osi odciętych. Funkcje te dotyczą stałej prędkości kątowej wirnika pompy ω.

Natężenie przepływu oblicza się korzystając ze wzoru

gdzie:

Q - natężenie przepływu,

V - objętość,

t - czas.

Prędkość cieczy w przewodzie oblicza się korzystając ze wzoru

gdzie:

v - prędkość przepływu,

Q - natężenie przepływu,

D - średnica przewodu.

Straty w przewodzie oblicza się korzystając ze wzoru

gdzie:

h_l - straty liniowe w przewodzie,

h_m - straty miejscowe w przewodzie.

Straty liniowe oblicza się ze wzoru

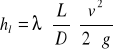
gdzie:

λ - współczynnik oporów liniowych,

L - długość przewodu,

v - prędkość przepływu,

D - średnica przewodu,

g - przyspieszenie ziemskie.

Straty miejscowe oblicza się ze wzoru

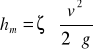
gdzie:

v - prędkość przepływu,

g - przyspieszenie ziemskie,

ζ - współczynnik oporów miejscowych.

Współczynnik oporów liniowych odczytujemy z wykresu Colebrooka-White'a.

Liczbę Reynoldsa obliczamy ze wzoru

gdzie:

υ - kinematyczny współczynnik lepkości,

V - prędkość przepływu,

D - średnica przewodu.

Chropowatość względną oblicza się ze wzoru

gdzie:

k - chropowatość bezwzględna,

D - średnica przewodu.

2. Opis Ćwiczenia

Do wykonania ćwiczenia wykorzystano stanowisko pomiarowe z układem dwóch pomp. Stanowisko składa się z:

- dwóch pomp wirnikowych GRUNDFOS Type UPS 25-40, P=80W

- zbiornika z wodą o wysokości zwierciadła h=0,6m ,

- czterech manometrów pudełkowych,

- watomierza,

- zamkniętego układu przewodów ciśnieniowych z zaworami odcinającymi.

Wartości przyjęte do obliczeń:

- prędkość obrotowa pompy ω = 1200 obr/min,

- średnica przewodu pierwszego D₁ = 2,54 cm = 0,0254 m,

- średnica przewodu drugiego D₂ = 3,81 cm = 0,0381 m,

- temperatura wody t = 20˚C,

- gęstość wody (w temp. 19,7^oC) ρ = 998,2033 kg/m³,

- kinematyczny współczynnik lepkości ν = 0,000001006 m³/s,

- współczynnik bezwzględnej chropowatości przewodów k = 0,0015 m,

- strata dla kolana ζ₁ = 0,51,

- strata dla trójnika ζ₂ = 2,4,

- strata dla zaworu ζ₄ = 0,15.

3. Obliczenia do ćwiczenia do pompy pojedynczej:

Poniżej znajdują się przykładowe obliczenia dla pierwszej serii pompy pojedynczej:

Współczynnik oporów liniowych odczytujemy z wykresu Colebrooke-White'a i wynosi on λ = 0,074.

Straty na przewodzie tłocznym i ssawnym między pompą a manometrem obliczamy ze wzoru na straty liniowe

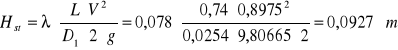
Wysokość ssania i tłoczenia obliczamy korzystając ze wzorów (odczyt z manometru podajemy w Pa oraz nie uwzględniamy wysokości zamocowania manometrów na przewodzie, gdyż zostało to uwzględnione przy odejmowaniu tła z manometrów)

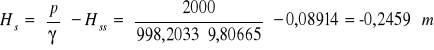
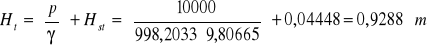
Wysokość podnoszenia pompy obliczamy korzystając ze wzoru

Moc użyteczną pompy obliczamy ze wzoru

Sprawność obliczamy korzystając ze wzoru

Obliczenia dla pomp połączonych wykonuje się analogicznie do tych z pompy pojedynczej, z tym że dla każdej pompy oddzielnie.

4. Rachunek błędów

W trakcie wykonywania doświadczenia mieliśmy do czynienia z różnymi rodzajami błędów. Były to między innymi błędy przyrządów oraz błędy odczytu. W celu wyznaczenia błędów obliczonych wielkości skorzystaliśmy ze wzoru na różniczkę zupełną:

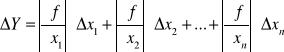
Ponadto zakładamy, że:

Δt = ± 0,5 s,

Δp = ± 0,0016 MPa,

ΔNp = ± 4 W,

Tab 4.1 - Wyniki błędów pojedynczej pompy

Lp	ΔQ [m³/s]	ΔHp [m]	ΔNu [W]	Δη [%]
1	0,0000363	0,0001064	0,000446	0,006725
2	0,0000360	0,0001162	0,000529	0,007223
3	0,0000326	0,0000570	0,000258	0,006916
4	0,0000284	0,0000401	0,000161	0,007427
5	0,0000201	0,0000475	0,000187	0,006164
6	0,0000129	0,0000314	0,000104	0,004174
7	0,0000111	0,0000250	0,000082	0,004100
8	0,0000109	0,0000236	0,000054	0,004422
9	0,0000092	0,0000218	0,000049	0,004238
10	0,0000058	0,0000191	0,000058	0,002924

Tab 4.2 - Wyniki błędów układu pomp podłączonych szeregowo

lp	ΔQ [m³/s]	ΔHp [m]	ΔNu [W]	Δη [%]
1	0,0000368	0,0000400	0,0001561	0,002558
2	0,0000346	0,0000387	0,0001422	0,002897
3	0,0000331	0,0000338	0,0001188	0,003154
4	0,0000320	0,0000354	0,0001202	0,003548
5	0,0000305	0,0000471	0,0001491	0,004289
6	0,0000290	0,0000584	0,0001663	0,004432
7	0,0000275	0,0000299	0,0000633	0,003596
8	0,0000260	0,0000497	0,0000686	0,002286
9	0,0000245	0,0000709	0,0000898	0,002121
10	0,0000230	0,0000564	0,0000668	0,002101

4. Wnioski

Według wyliczeń najlepszymi parametrami, które dają najbardziej optymalne warunki pracy pompy pojedynczej są: wydatek Q = 0,0004347826 m³/s oraz wysokość podnoszenia H_p=1,4344 m, ponieważ w tych warunkach pompa osiąga maksymalną sprawność η=21,1 % przy pobieranej mocy N_p=30 W.

Z kolei przy połączeniu pomp szeregowych otrzymano następujące optymalne parametry: wydatek Q = 0,0002353 m³/s, wysokość podnoszenia H_p=4,15 m. W tych warunkach agregat pompowy osiąga maksymalną sprawność η=17,4% przy pobieranej mocy N_p= 9,56W. Z analizy wykresu wynika, więc, że najkorzystniejsze warunki pracy pompy nie są wcale przy jej maksymalnym obciążeniu.

Wyniki, jakie otrzymano nie zgadzają się z tymi, które powinno się otrzymać. Powodem, dla którego tak się stało były zapewne między innymi brudne przewody, które przez długi czas nie były czyszczone, błędy odczytu, błędy przyrządów (w tym bardzo małe skoki wskazówek manometrów oraz watomierza dla małych przepływów).

- 4 -

---