2. Obliczamy rezystancję krytyczną ze wzoru:
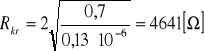
![]()
3. Miejsca geometryczne
a) stałe L, C
Obliczamy współczynnik tłumienia na podstawie wzoru:
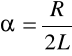
oraz pulsację drgań własnych z logarytmicznego dekrementu tłumienia:
(w tabeli 3 obliczono dekrement tłumienia - do wzoru potrzebny jest nam jego logarytm)
![]()
![]()
gdzie:
Wyniki obliczeń zestawiono w tabeli 5.
Tabela 5.
α |
ω0 |
285,7143 |
267,023 |
357,1429 |
310,559 |
428,5714 |
342,857 |
500 |
359,712 |
571,4286 |
363,967 |
642,8571 |
371,594 |
714,2857 |
379,939 |
785,7143 |
392,857 |
857,1429 |
394,997 |
928,5714 |
391,802 |
1000 |
374,532 |
1071,429 |
324,675 |
Na podstawie tabeli 5 rysujemy wykres ωN = f(α) (rys.3).
b) stałe R, L
Obliczamy pulsację drgań nietłumionych:
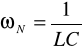
Obliczamy współczynnik tłumienia na podstawie wzoru:
![]()
(w tabeli 4 obliczono dekrement tłumienia - do wzoru potrzebny jest nam jego logarytm)
Wyniki obliczeń zestawiono w tabeli 6.
Tabela 6.
ωN |
α |
10769231 |
11846154 |
6086957 |
7973913 |
4242424 |
6830303 |
3255814 |
6609302 |
2641509 |
6339623 |
2222222 |
6022222 |
1917808 |
6252055 |
Na podstawie tabeli 6 rysujemy wykres ωN = f(α) (rys.4).
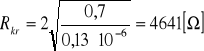
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka