![]()
Sprawozdanie z ćwiczenia nr C11
Temat: Pomiar długości fali za pomocą siatki dyfrakcyjnej i spektrometru.
Podstawy teoretyczne.
Fale elektromagnetyczne są to rozchodzące się w przestrzeni periodyczne zmiany pola elektrycznego i magnetycznego. Falę taką można zapisać za pomocą funkcji falowej
![]()
gdzie ![]()
- amplituda, (t-kx) - faza fali, - częstość kołowa,
k - liczba falowa związana z długością fali ![]()
.
Fala posiada również okres. Okres jest to czas, w którym fala przebiega odległość równą jednej długości fali.
Długość fali jest to odległość między dwoma najbliższymi punktami przestrzeni, w których fala ma tą samą fazę.
Interferencja fali jest to zjawisko powstające podczas nałożenia się dwóch lub więcej fal w danym punkcie przestrzeni.
Obraz interferencyjny można uzyskać za pomocą siatki dyfrakcyjnej.
Siatką dyfrakcyjną nazywamy układ wielu szczelin równoległych do siebie rozmieszczonych w równych odstępach. Najprostszą siatkę realizuje się poprzez nacięcia na płytce szklanej ciągu równoległych rys odgrywających rolę przesłon.
Stałą siatki d nazywamy sumę szerokości szczeliny i odstępu między szczelinami.
Różnica dróg promieni wychodzących z dwóch sąsiednich szczelin, ugiętych pod tym samym kątem wynosi
![]()
Fale wzmacniają się (padając w jeden punkt), gdy różnica ich dróg równa jest wielokrotności długości fali . Warunek wzmocnienia można więc zapisać
![]()
Położenie maksimów zależy zatem od długości fali, co pozwala na rozseparowanie składowych światła białego i wyznaczenie ich długości przez pomiar kąta ugięcia odpowiadający maksimum, przy znanej wartości stałej siatki d. Obrazuje to wzór
![]()
Liczba k określa tzw. rząd widma, a więc mówimy np. o widmie rzędu pierwszego (dla k=1) itd. Prążek zerowy ma barwę światła użytego.
Widma poszczególnych rzędów dla światła "białego" składają się z prążków barwnych odpowiadających długościom fal użytego światła rozłożonych symetrycznie względem prążka zerowego.
Jak wiemy siatkę dyfrakcyjną można wykorzystać do rozdzielenia fal o różnych długościach jednak to jaka może być najmniejsza różnica między długościami fal , tak aby można je było rozróżnić określa tzw. zdolność rozdzielcza R zdefiniowana jako
![]()
gdzie jest jedną z długości dwu linii widmowych a
![]()
jest różnicą dłg. fal między nimi.
Warunkiem na rozdzielenie dwóch fal o bliskich sobie długościach jest
kryterium Rayleigha, które mówi, że aby dwa maksima główne były rozróżnialne, to odległość kątowa powinna być taka, aby minimum jednej linii przypadało w maksimum drugiej. Stąd
![]()
gdzie m - rząd widma, N - liczba szczelin.
Wykonanie ćwiczenia.
1. Ustawienie spektrometru :
- nastawienie krzyża lunety na ostrość
- nastawienie lunety na nieskończoność tzn. na ostrość obrazu dalekiego przedmiotu
- nastawienie kolimatora na ostry obraz oświetlonej szczeliny (wtedy szczelina jest w ognisku soczewki kolimatora).
- wypoziomowanie stolika spektrometru
2. Ustawiamy siatki dyfrakcyjnej pionowo i prostopadle do osi kolimatora W tym celu oświetlamy szczelinę kolimatora światłem sodowym i obserwujemy widma dyfrakcyjne po obu stronach prążka zerowego. Prostopadłe ustawienie siatki sprawdzamy, mierząc kąty ugięcia dla tego samego rzędu po obu stronach siatki. Równość kątów świadczy o prawidłowym ustawieniu siatki.
3. Oświetlamy siatkę dyfrakcyjną źródłem światła o znanej długości fali. W naszym wypadku użyliśmy lampy sodowej.
Następnie wyznaczamy stałą siatki d posługując się wzorem
![]()
stąd otrzymujemy
![]()
4. Oświetlamy siatkę dyfrakcyjną badanym źródłem światła tzn. lampą neonową, a następnie wyznaczamy długość fali dla wielu prążków Neonu : czerwony 1, czerwony 2, żółty, zielony, poprzez pomiar kąta odchylenia prążka zarówno po lewej jak i po prawej strone osi optycznej kolimatora.
Długości tych fal obliczamy ze wzoru:
![]()
Otrzymaliśmy następujące długości fal dla badanych prążków Neonu, które porównujemy z wartościami w tablicach. Obrazuje to poniższa tabela:
Kolor prążka |
Długość fali z pomiarów |
Długość fali z tablic |
Czerwony 1 |
649,419,9 |
640,2 |
Czerwony 2 |
614,219,9 |
614,3 |
Żółty |
596,019,9 |
585,2 |
Zielony |
554,619,9 |
540,0 |
Dyskusja błędów.
1.Znajdujemy błąd wynikający z dokładności odczytu
![]()
gdzie 2' - dokładność odczytu kąta
![]()
- szerokość kątowa szczeliny
Wynosi ona:
- dla Sodu ![]()
- dla Neonu ![]()
2. Znajdujemy błąd ![]()
z poniższego wzoru
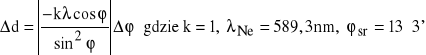
po podstawieniu otrzymujemy
![]()
a ![]()
czyli stała siatki d=(2678,352,8) nm
3. Znajdujemy błąd ![]()
ze wzoru
![]()
Uwaga! Pochodną cząstkową po k pomijamy bo wynosi 0.
Czyli otrzymujemy
![]()
Oznacza to, że długości fal kolejnych prążków Neonu wynoszą:
- dla czerwonego 1 =(649,419,9) nm
- dla czerwonego 2 =(614,219,9) nm
- dla żółtego =(596,019,9) nm
- dla zielonego =(554,619,9) nm
Interpretacja wyników i wnioski.
1. Można zauważyć, że rozszczepiając światło za pomocą siatki dyfrakcyjnej układ kolejnych prążków barwnych jest odwrotny niż w pryzmacie: najbliżej prążka zerowego położony jest prążek fioletowy a najdalej - czerwony, odpowiadający najdłuższej fali widzialnej.
2. Dla niewielkich kątów ugięcia sinus kąta można zastąpić przez jego tangens
![]()
gdzie x - przesunięcie liniowe na ekranie badanego prążka, względem prążka zerowego.
l - odległość siatki od ekranu.
Uwzględniając powyższe w przekształceniu wzoru: dsin=k (dla k=1) otrzymujemy
![]()
Wynika z tego, że liniowe przesunięcie prążka na ekranie zwiększa się z długością fali, co dowodzi słuszności wniosku 1-go.
Laboratorium z Fizyki.
3