Politechnika Krakowska		rok: 1998/99	nr ćwiczenia
Fizyka Techniczna	MARCIN	semestr: I	42
Grupa: C	KUK	Ocena:	Podpis:
Zespół: 8

Pomiar współczynnika absorpcji promieni
emitowanych przez
w równowadze promieniotwórczej z
w glinie przy użyciu licznika Geigera - Műllera.

1. Teoria.

Promienie
pierwiastków radioaktywnych stanowią strumienie elektronów o prędkościach zmieniających się w sposób ciągły od 0 do pewnej wartości maksymalnej, charakterystycznej dla danego pierwiastka. Ich zdolność jonizacyjna i przenikliwość zależą od energii. Promienie o dużych energiach (do 3 Me V) tzw. twarde, przenikają przez blachy Al. grubości kilku milimetrów i warstwy powietrza grubości kilku metrów. Podczas przechodzenia przez materię cząstki
tracą energią na skutek oddziaływań z atomami absorbenta i zmieniają kierunek ruchu. Strumień elektronów rozprasza się i ulega absorpcji. Doświadczenia mówi, że wiązka równoległych promieni
o natężeniu
po przejściu warstwy substancji grubości
posiada natężenie
wyrażające się wzorem:

gdzie
nazywa się współczynnikiem absorpcji promieni
danego pierwiastka radioaktywnego dla badanej substancji, np. Al. Jednostką
jest
.

W naszym ćwiczeniu cząstki
powstają na skutek rozpadu kilku pierwiastków należących do szeregu promieniotwórczego uranu
(okres połowicznego rozpadu
lat).

Uran
wskutek emisji cząstek
przechodzi w
(UX, T=241 dni), który w dalszym ciągu emituje cząstki
oraz promienie
i przechodzi w
Pa (
, T=1,14 min) również promieniotwórczy.

Pierwiastek ten emituje dwie grupy cząstek
o dwóch różnych energiach maksymalnych ( 2,31 Me V i 1,52 Me V), a zatem różnych współczynnikach absorpcji, jednak cząstki o dużej energii (2,31 Me V) stanowią ułamek procentu całego promieniowania
. Również pozostałe grupy promieni
pochodzące od dalszych członów szeregu uranowego, jakkolwiek występujące w większych ilościach, nie wpływają na wyniki pomiaru, ponieważ są tak „miękkie”, że zostają zaabsorbowane przez płytki Al. o grubości około 0,1 mm.

W celu wyznaczenia
przykrywamy źródło promieni
(warstewkę ciała radioaktywnego) kolejno płytkami blachy aluminiowej o różnych grubościach x i mierzymy liczbę cząstek
przechodzących w minucie przez płytkę. Pisząc równanie
dla warstw o grubościach
i
i logarytmując je stronami, mamy:

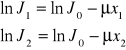
stąd:

Postępowanie dokładniejsze polega na mierzeniu natężeń przy stopniowo wzrastającej grubości absorbenta i sporządzeniu wykresu ilJ jako funkji x. Wykres ten, jak widać z równania :

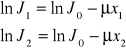
powinien być linią prostą. Obieramy na prostej 2 dostatecznie odległe punkty i wstawiając do:

dane odczytane z wykresu, obliczamy
. Wykres lnJ=f(x) odbiega od prostej w przypadku, gdy promieniowanie
pierwiastka jest mieszaniną 2 lub więcej grup promieni znacznie różniących się współczynnikiem absorpcji.

Przystępując do pomiarów licznikowych należy zwrócić uwagę na następujące okoliczności: rozkład w czasie cząstek jonizujących, wpadających do licznika, jest przypadkowy. Jeżeli 2 cząstki wpadają po sobie w odstępie czasu krótszym od „czasu martwego” licznika, wówczas są policzalne jako jedna. Ilość takich pominiętych cząstek rośnie wraz z ilością cząstek wpadających w jednostce czasu. Rzeczywista ilość wpadających cząstek jest większa od wskazań przelicznika. Przyjmiemy jednak, że przy przeliczniku elektronowym i zliczeniach kilkuset cząstek na minutę błąd ten jest do pominięcia.

Przed rozpoczęciem pomiarów należy też ustalić z jakim błędem chcemy wielkość mierzoną uzyskać. Według teorii prawdopodobieństwa błąd średni
obserwowanej ilości N zdarzeń przypadkowych wynosi:

Błąd procentowy:
. Jeżeli chcemy znać N z dokładnością np. 5%, to musimy obserwować około 400 impulsów, jeżeli z dokładnością 1% - już 10 000. Jeżeli licznik przy danym natężeniu promieniowania liczy np. 50 impulsów na minutę, to obserwacja w I przypadku musi trwać
minut, w II
minut. Błąd średni sumy lub różnicy wyników dwóch pomiarów
i
wynosi:

.

W celu pomiaru liczby cząstek jonizujących, wpadających do licznika w 1 minucie postępujemy następująco:

• Wyznaczamy tzw. tło licznika, tj. liczbę cząstek zliczonych w jednej minucie bez preparatu radioaktywnego; pochodzą one od zanieczyszczeń radioaktywnych w otoczeniu i w materiale licznika, od promieniowania kosmicznego i innych przyczyn.

• Wyznaczamy liczbę zliczeń
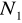
  w obecności preparatu radioaktywnego, przysłoniętego płytką absorbującą o danej grubości x.

• Ponieważ nasz preparat prócz cząstek
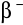
  wysyła jeszcze dość przenikliwe promieniowanie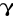
  , na które licznik reaguje, chociaż z małą wydajnością, należy uwzględnić udział tego promieniowania w rejestrowanych impulsach, chociażby w sposób przybliżony. Przysłąniamy w tym celu źródło płytką aluminiową grubości 3-4 mm, tak by wszystkie cząstki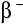
  były zaabsorbowane, a pozostały tylko promienie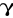
  . Stwierdzamy to w ten sposób, że dokładanie dalszych 1-2 mm Al. nie zmienia ilości zliczeń w minucie. Cząstki rejestrowane obecnie pochodzą od „tła” i promieni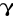
  . Oznaczamy ich ilość łączną w minucie przez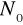
  .

• Różnica
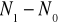
  podaje liczbę cząstek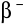
  zarejestrowanych w minucie przez licznik

1. Doświadczenie.

Błąd systematyczny grubości absorbera
.

Błąd średni
różnicy dwóch pomiarów wynosi

Opracowanie wyników pomiaru wielkości zależnych liniowo.

Współczynniki: a, b obliczamy posługując się metodą regresji liniowej.

n- liczba pomiarów

Lp.
1	3,416662232	55,16815127	0,2116	7,427526592	0,46
2	3,857504723	51,98827037	0,286225	7,210289201	0,535
3	4,359337746	51,07182365	0,3721	7,146455321	0,61
4	6,670117561	38,85969803	1,1449	6,23375473	1,07
5	8,045678372	27,653014	2,3409	5,258613315	1,53
6	8,278320744	26,76976341	2,56	5,173950465	1,6
7	8,140803973	23,62136398	2,805625	4,860181476	1,675
8	8,298670291	22,48748689	3,0625	4,742097309	1,75
9	8,198059837	13,76060791	4,8841	3,709529338	2,21
10	7,48322153	7,855153595	7,1289	2,802704693	2,67
Suma	66,74837701	319,2353331	24,79685	54,56510244	14,11

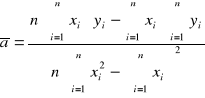
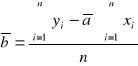
Po obliczeniu parametrów a i b prostej należy obliczyć ich odchylenie standardowe Sa i Sb.

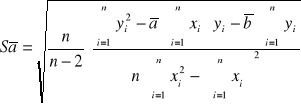
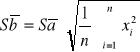
Lp.	Grub. kol. płyt. Absorb. [mm]	Grubość absorb. [mm]	Czas obs.	N	N (1 min.)	N-N0	ln(N-N0)
N0	3,68		02:00,0	580	290
tło	Tło		14:59,9	1977	132
	Glin
1	0,46	0,46	01:59,9	3940	1972	1682	7,43	47,56	0,03
2	0,075	0,535	02:00,6	3303	1643	1353	7,21	43,97	0,03
3	0,075	0,61	01:59,3	3101	1560	1270	7,15	43,01	0,03
4	0,46	1,07	01:59,6	1594	800	510	6,23	33,01	0,06
5	0,46	1,53	01:59,2	958	482	192	5,26	27,79	0,14
6	0,07	1,6	02:00,1	934	467	177	5,17	27,51	0,16
7	0,075	1,675	01:59,7	836	419	129	4,86	26,63	0,21
8	0,075	1,75	01:59,8	808	405	115	4,74	26,36	0,23
9	0,46	2,21	02:00,1	662	331	41	3,71	24,92	0,61
10	0,46	2,67	02:00,2	614	306	16	2,80	24,42	1,48
Miedź
1	0,06	0,06	02:00,1	4839	2417	2127	7,66	52,03	0,02
2	0,06	0,12	02:00,0	3191	1596	1306	7,17	43,43	0,03
3	0,06	0,18	01:59,3	2234	1124	834	6,73	37,60	0,05
4	0,06	0,24	01:59,9	1692	847	557	6,32	33,72	0,06
5	0,06	0,3	01:59,9	1258	630	340	5,83	30,33	0,09
6	0,06	0,36	01:59,3	1048	527	237	5,47	28,58	0,12
7	0,06	0,42	02:00,1	838	419	129	4,86	26,62	0,21
8	0,06	0,48	02:00,1	732	366	76	4,33	25,61	0,34
9	0,06	0,54	02:00,9	700	347	57	4,05	25,24	0,44
10	0,06	0,6	02:00,1	680	340	50	3,91	25,09	0,50

Wyliczenie współczynnika absorpcji pierwszego materiału:

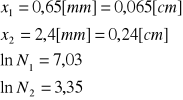
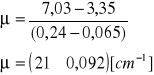
Współczynnik absorpcji w przybliżeniu odpowiada współczynnikowi glinu. (Tab. 17[cm^-1])

Wyliczenie współczynnika absorpcji drugiego materiału:

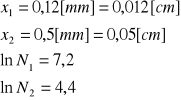
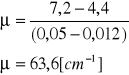
Współczynnik absorpcji w przybliżeniu odpowiada współczynnikowi miedzi i mosiądzu. (Tab. 56[cm^-1])

Wyznaczenie prostokątów niepewności pomiarowej.

Błąd systematyczny: Δx=0,005[mm]

Wnioski:

Błędy występujące w doświadczeniu spowodowane są przede wszystkim przez brak zitegrowania licznika z czasomierzem. Wyniki tabicowe współczynnika absorbcji dla glinu i miedzi nie mieszczą się w przedziale wyliczeń.

1

5

---