Wydział: FTiMK	Imie i Nazwisko: Marcin Wiśniowski	Nr. Zepołu 8	Ocena Ostateczna
Grupa: Trzecia	Tytół ćwiczenia: Wyznaczanie przyspieszenia ziemskiego przy użyciu wachadła prostego	Nr. Cwiczenia 1	Data Wykonania: 05.10.2001

1. Wprowadzenie

Przyspieszenie ziemskie g jest to przyspieszenie ciał swobodnie spadających w polu grawitacyjnym Ziemi, tj. przy braku oporów ruchu.

Z prawa powszechnej grawitacji Newtona można wyliczyć, że na powierzchni Ziemi jego wartość dana jest wzorem:

gdzie G jest stałą grawitacji, M­­_Z­ i R_­Z są odpowiednio masą i promieniem Ziemi. Zatem na biegunach, gdzie promień naszej planety jest najmniejszy, będzie ono miało największą wartość. Zmiana wartości przyspieszenia g wraz z szerokością geograficzną jest nie tylko wynikiem kształtu ziemi. Na efektywną g wpływa również jej ruch obrotowy. Związane z nim przyspieszenie ziemskie na wszystkich szerokościach geograficznych wyjątkiem biegunów. Oczywiście wartość przyspieszenia ziemskiego maleje wraz z wysokością nad powierzchnią Ziemi.

2. Metoda pomiaru

Wartość przyspieszenia ziemskiego możemy wyznaczyć wykożystójąc prawa ruchu

wahadła prostego. Wahadło proste to kulka zawieszona na nie rozciągliwej, lekkiej nici, której ciężar możemy zaniedbać. Wychylona z położenia równowagi i swobodnie puszczona kulka wykonuje ruch drgający prosty. Okres drgań takiego wahadła jest określony zależnością:

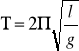
gdzie l to długość wahadła, g to przyspieszenie ziemskie. Lecz założenie to jest spełnione wówczas gdy kąt wychylenia wahadła ϕ jest mniejszy od 5°. Powyższe równanie pozwala na wyznaczenie przyspieszenia ziemskiego, jeśli znamy długość wahadła l i okres jego drgań Τ:

3. Tabele pomiarowe i obliczenia.

Lp	10T[s]	T[s]	(Ti-T) [s]	(Ti-T)^2 [s]	Lp	S [m]	2r [m]
1	18,8	1,88	0,021	0,000441	1	0,874	0,0188
2	18,4	1,84	- 0,019	0,000361	2	0,869
3	18,8	1,88	0,021	0,000441	3	0,864
4	19,0	1,90	0,041	0,001681	4	0,866
5	18,1	1,81	- 0,049	0,002401	5	0,865
6	18,8	1,88	0,021	0,000441	6	0,866
7	18,2	1,82	- 0,039	0,001521	7	0,864
8	19,0	1,90	0,041	0,001681
9	18,4	1,84	- 0,019	0,000361
10	18,4	1,84	- 0,019	0,000361

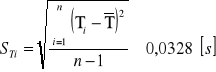
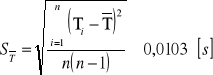
Δ_dT = 0,1 [s]

r = 0,0094 [m]

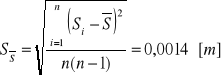
4. Błędy pomiarowe

• Niepewność kwadratowa przyspieszenia ziemskiego:

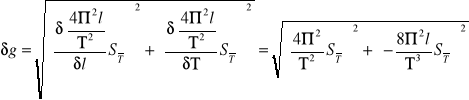
• Niepewność maksymalna

• Niepewność procentowa

Ostateczny wynik przyciągania ziemskiego:

5. Wnioski:

g zmierzone i wyliczone z ćwiczenia:

g z tablic fizycznych dla Krakowa:

porównując wyniki otrzymane i tablicowe zauważamy że wyniki są zbliżone. Wynika z tego to, że metoda którą zastosowaliśmy jest poprawna. Jednak ta rozbieżność wyników może być spowodowana:

• Zaniedbaniem oporu powierza

• Niedokładność przyrządów pomiarowych lub osób posługujących się nimi

---