Liczby zespolone.

1. Elementarne pojęcie liczby zespolonej.

Liczbą zespoloną nazywamy zbiór liczb rzeczywistych w postaci z=x+iy gdzie i²= -1.

x=Re(z) - część rzeczywista

y=Im(z) - część urojona

2. Działania na zbiorze liczb zespolonych.

1. Suma liczb zespolonych.

(x+iy)±(x'+iy')=x±x'+i(y±y')

(2-i)+(1+3i)=3+2i

2. Iloczyn liczb zespolonych.

(x+iy)(x'+iy')=xx'-yy'+i(xy'+x'y)

(1+i)²(1-3i)=(1+2i-1)(1-3i)=6+2i

3. Dzielenie liczb zespolonych.

Uwaga: aby podzielić dwie liczby zespolone należy pomnożyć je przez liczbę sprzężoną z dzielną

z*z_sp=x²+y²

3. Interpretacja geometryczna liczby zespolonej.

Dla każdej liczby zespolonej istnieje punkt o współrzędnych (x, y). Obrazem liczby zespolonej jest wektor w=[x, y].

Modułem liczby zespolonej nazywamy długość wektora w.

Argumentem liczby zespolonej nazywamy kąt ϕ zawarty między wektorem w a osią X.

arg z=ϕ -Π ≤ ϕ ≤ Π

Argumentem liczby z nazywamy θ=ϕ + 2kΠ k∈<-∞, ... , -2, -1, 0, 1, 2, ... ,∞>.

Arg z = arg z + 2kΠ

4. Potęga, wzory MOIVRE'a.

1. Własności modułu i argumentu liczby zespolonej.

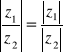
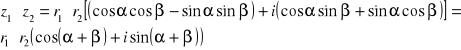
5. Pierwiastek liczby zespolonej.

Założenie:

z=?

k = 0, 1, 2, ... , n-1.

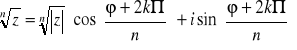
, dla k=0 pierwiastek główny.

6. Postać wykładnicza liczby zespolonej (EULER'a).

- postać wykładnicza liczby zespolonej.

Korzystając z postaci wykładniczej obliczyć

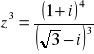
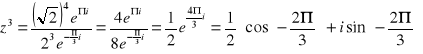
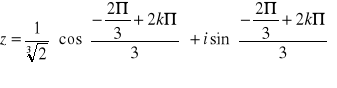
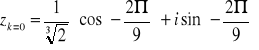
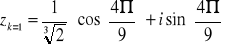
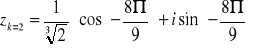
Graficzne rozwiązanie zadania.

Funkcja zmiennej zespolonej.

f(z)=

- część rzeczywista funkcji f(z)

- część urojona funkcji f(z)

Funkcję f(z) nazywamy analityczną jeżeli posiada pochodną, tzn. istnieje funkcja

Przykłady.

1.

2. f(z)=z* (z* - funkcja sprzężona)

dla Δx=0

dla Δy=0

Funkcja f(z*) nie jest analityczna.

3.

Funkcja wykładnicza zmiennej zespolonej

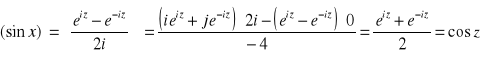
Logarytm funkcji zmiennej zespolonej

r - moduł liczby zespolonej z

Całkowanie funkcji zmiennej zespolonej

z=x+iy

dz=dx+idy

d(uv)=(du)v+u(dv)

dla r=1

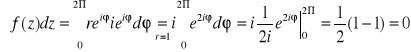
Matematyka - Liczby zespolone i funkcja zmiennej zespolonej

- 5 -

---