![]()
![]()
Ruch wahadła matematycznego o długości l wychylonego z położenia równowagi można opisać równaniem różniczkowym , które otrzymuje się z II zasady dynamiki Newtona.
![]()
Gdzie: ϕ - kąt wychylenia od położenia równowagi , t - czas i g - przyspieszenie ziemskie. Równanie to jest nieliniowym równaniem różniczkowym drugiego rzędu. Jego rozwiązanie otrzymuje się metodami numerycznymi , po zastąpieniu funkcji sinus jej rozwinięciem w szereg potęgowy względem kąta ϕ (wyrażonego w radianach):
![]()
Jeżeli ograniczymy się do małych wychyleń , dokładne jest wtedy przybliżenie sinϕ ≈ ϕ i pierwsze równanie sprowadza się do postaci:
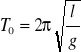
Jest to równanie różniczkowe liniowe , właściwe dla oscylatora harmonicznego. Opisuje ono małe drgania wahadła matematycznego o częstotliwości kołowej ω02=g/l i okresie drgań :
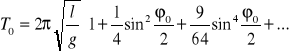
Rozwiązaniem równania trzeciego jest funkcja ϕ ϕ0sin(ω0/lδ), gdzie ϕ0 jest amplitudą drgań . Przy większych wychyleniach , gdy przybliżenia sinϕ ≈ ϕ nie można stosować , rozwiązanie staje się bardziej skomplikowane . Wahadło staje się oscylatorem nieliniowym i w wyrażeniu na wychylenie ϕ pojawiają się składniki zawierające wielokrotność częstości ω0. Okres wahań wahadła można wtedy wyrazić wzorem:
Wzór ten z dobrym przybliżeniem można przedstawić w postaci:
Gdzie: A=ϕ0. Gdy A dąży do zera , co odpowiada przypadkowi małych wychyleń , T(A) przyjmuje wartość T0 .

![]()
Zmiany okresu wahań wraz ze zmianą amplitudy można przedstawić za pomocą bezwymiarowej wielkości :
Dla małych wychyleń (A≈0), f(A)=0. W celu wyznaczenia funkcji f(A) mierzymy średnie okresy wahań da serii wahnięć rozpoczynanych od różnych amplitud. Ponieważ amplituda wahań maleje w czasie pomiaru , wielkość A w ostatnim wzorze zastępujemy wartością średnią Aśr. Jest ona równa średniej arytmetycznej amplitudy początkowej A1 i amplitudy ostatniego wahnięcia A2 w danym pomiarze.
Wykres funkcji f(Aśr) stanowi graficzny obraz względnych zmian okresu wahań. Punkt początkowy wykresu posiada współrzędne Aśr=0,f(0)=0. Różnica f(Aśr)-f(0) jest miarą nieliniowości wahadła.
Tabela 1.
Długość wahadła „l” wynosi 0,33 m.
L.p. |
Liczba wahnięć n |
Czas t [s] |
f(A0) |
Okres T(A0) [s] |
1 |
30 |
35,8 |
0,0356 |
1,193 |
2 |
30 |
35,4 |
0,0243 |
1,18 |
3 |
30 |
35,6 |
0,03 |
1,187 |
4 |
30 |
35,5 |
0,028 |
1,184 |
5 |
30 |
35,7 |
0,033 |
1,19 |
6 |
30 |
35,4 |
0,0243 |
1,18 |
7 |
30 |
35,3 |
0,0217 |
1,177 |
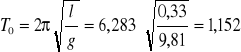
Tabela 2.
1o=0,035 rad.
f(A) |
L.p |
Amplituda |
Liczba wahnięć n |
Czas t [s] |
Okres T(A) [s] |
||
|
|
A1 |
A2 |
Aśr |
|
|
|
0,054 |
1 |
5 |
4,3 |
4,65 |
20 |
24,3 |
1,215 |
0,0633 |
2 |
15 |
14,5 |
14,75 |
20 |
24,5 |
1,225 |
0,0633 |
3 |
25 |
24,3 |
24,65 |
20 |
24,5 |
1,225 |
0,072 |
4 |
35 |
33,3 |
34,15 |
20 |
24,7 |
1,235 |
0,098 |
5 |
45 |
42,5 |
43,75 |
20 |
25,3 |
1,265 |
0,089 |
6 |
55 |
51,5 |
53,25 |
20 |
25,1 |
1,255 |
0,132 |
7 |
65 |
59 |
62 |
20 |
26,1 |
1,305 |
T(Aśr) |
f(Aśr) |
T'(Aśr) |
f'(Aśr) |
1,215 |
0,054 |
1,154 |
0,0017 |
1,225 |
0,0633 |
1,171 |
0,0165 |
1,225 |
0,0633 |
1,207 |
0,047 |
1,235 |
0,072 |
1,263 |
0,096 |
1,265 |
0,098 |
1,343 |
0,166 |
1,255 |
0,089 |
1,451 |
0,26 |
1,305 |
0,132 |
1,582 |
0,373 |
Dyskusja wyników:
Pomiary zostały przeprowadzone w sposób dość dokładny, błędy pomiaru mogą wystąpić dla dużych amplitud , gdyż podczas wprawiania wahadła w ruch występowały nie pożądane drgania poprzeczne wahadła.
1
1
![]()
![]()
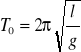
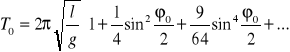
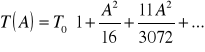
![]()
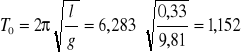
Wyszukiwarka