Na początek rozwiążemy takie zadanie. Mamy daną zmienna losową dwuwymiarową okresloną wzorem:

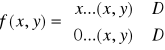
Pierwsza część zadania polegać będzie na znalezieniu stałej

c, gestości rozkładu brzegowego od x, czyli fx(x), a także

fy(y), oraz warunek f(x|y=1/2). Z kolei druga część zadania będzie

polegała na sprawdzeniu, czy x i y są skorelowane i niezależne.

Sprawdzić to można obliczając EX, EY,
.

Skupmy się na razie na pierwszej części. Można wyliczyć w

pamięci ile będzie wynosiła stała c, a będzie ona wynosiła 2.

fx(x) dla
będzie równa:

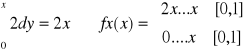
Z kolei fy(y) będzie równa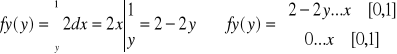
. Teraz liczymy warunek: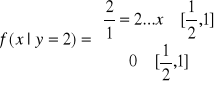
.

I teraz aby policzyć COV(X, Y) i sprawdzić, czy x i y są niezależne i skorelowane, liczymy kolejno:

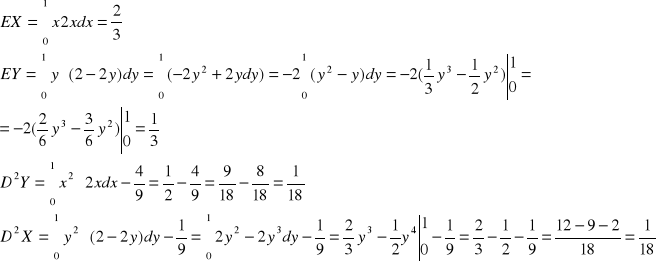
Mając te dane można obliczyć COV(X, Y), oraz prostą regresji mówiącą o niezależności i skorelowaniu. A zatem:

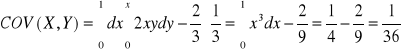
Pracą domową będzie dokończenie powyższego zadania, oraz wykonanie analogicznego z takim rysunkiem:

Z tym że warunek ma być f(x|y=1).

1

1

D

2

2

---