Miary dla populacji i próby (estymacja punktowa)

Populacją generalną nazywamy skończoną lub nieskończoną zbiorowość, w stosunku do której mogą być sformułowane wnioski.

Próbą jest natomiast skończona część populacji podlegająca badaniu statystycznemu.

Sposób wyboru elementów z populacji: próba reprezentatywna - wnioski wyprowadzone na podstawie próby będą wiarygodne, losowanie - losowość, niezależność, liczebność - wielkość próby.

Próba losowa prosta to próba, w której każdy układ n elementów populacji ma to samo prawdopodobieństwo reprezentowania populacji oraz wybór jakiegokolwiek elementu z populacji do próby nie zmienia prawdopodobieństwa wyboru pozostałych elementów; losowanie niezależne - zwrotne (ze zwracaniem), zależne - bezzwrotne (bez zwracania).

Skala nominalna - do umieszczania osobników w różnych grupach systematycznych (małe, duże - wymaga określenia dokładnego progu - skala nominalna dychotomczna - dwa podzbiory), porządkowa - dokładniejsza, przyporządkowuje kolejność (rangi), interwałowa - przypisuje elementom wartość mierzoną w ściśle określonych jednostkach.

Statystyką nazywamy dowolną funkcję zmiennych losowych X₁, X₂, ..., X_n, stanowiących próbę i nie zawierającą nieznanych parametrów.

Miary charakterystyki statystyki położenia, rozproszenia i kształtu.

Miary położenia dla próby: średnia arytmetyczna, ważona, geometryczna i harmoniczna (wzory napisane w kolejności nazw).

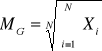
Parametry rozkładu zmiennych losowych (miary położenia i rozrzutu - rpozproszenia dla populacji)

Wybrana miara położenia

Wartość oczekiwana zmiennej losowej (wartość przeciętna, średnia, nadzieja matematyczna, moment zwykły pierwszego rzędu - środek ciężkości masy rozkładu prawdopodobieństwa).

dla zmiennej losowej dyskretnej

E(X)

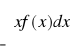
dla zmiennej losowej ciągłej

Miary rozproszenia

1. Wariancja zmiennej losowej (moment centralny drugiego rzędu) - wartość oczekiwana kwadratu odchylenia zmiennej losowej X od jej wartości oczekiwanej.

dla zmiennej losowej dyskretnej

D²(X)

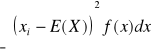
dla zmiennej losowej ciągłej

2. Odchylenie standardowe

3. Współczynnik zmienności (charakteryzuje rozrzut - rozproszenie, podobnie jak wariancja i odchylenie standardowe)

Statystyki (miary położenia i rozrzutu - rozproszenia dla próby)

Miary położenia

Średnia w próbie (średnia arytmetyczna obserwacji)

Mediana (M_e) jest wartością środkową w przypadku nieparzystej liczby obserwacji lub średnią dwóch wartości środkowych w przypadku parzystej liczby obserwacji. Obserwacje muszą być uporządkowane od najmniejszej do największej - szereg pozycyjny.

Moda (dominanta)

x_i - dla którego p_i = P(X=x_i) osiąga maksimum dla zmiennej losowej dyskretnej

x₀ - dla którego funkcja f(x) osiąga maksimum dla zmiennej ciągłej

Kwartyl dolny (Q₁) to mediana tych obserwacji, które nie są większe od mediany w całej próbie.

Kwartyl górny (Q₃) to mediana tych obserwacji, które nie są mniejsze od mediany w całej próbie.

Średnia ucięta to średnia arytmetyczna obserwacji w próbie po usunięciu z niej obserwacji największych i najmniejszych w określonej proporcji (zazwyczaj 5%).

Rozstęp (R) w próbie, to różnica między obserwacją największą i najmniejszą

Miary rozproszenia

Wariancja z próby (średnie odchylenie kwadratowe) z próby to statystyka określona wzorem:

lub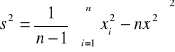

Odchylenie standardowe z próby, to pierwiastek kwadratowy ze średniego odchylenia kwadratowego

Współczynnik zmienności

Przy obliczaniu momentów z szeregu rozdzielczego dla cechy ciągłej zwykle zakłada się, że wszystkie wartości z próby należące do pewnego przedziału klasowego leżą w środkowym punkcie tego przedziału.

, dla cechy dyskretnej (l_i - liczebność klasy, x_i - wart. zmiennej los w klasie)

, dla cechy ciągłej (
- wart. zmiennej los dla środka i-tego przedziału kl.)

W związku z tym obliczone wartości momentów szeregu rozdzielczego są tylko pewnym przybliżeniem momentów wyznaczonych z próby. Przybliżenie jest zależne od długości przedziałów klasowych i jest lepsze, gdy te długości przedziałów są mniejsze. w celu poprawienia obliczonych wartości momentów stosujemy poprawki Shepparda (odejmujemy od wartości momentu).

poprawka Shepparda dla momentu centralnego drugiego stopnia

Podsumowanie

Średnia arytmetyczna wyliczona z próby jest odpowiednikiem wartości oczekiwanej (w populacji). W języku matematycznym trzeba by napisać: Średnia arytmetyczna wyliczona z próby jest estymatorem wartości oczekiwanej (w populacji).

Średnie odchylenie kwadratowe (wariancja z próby) jest estymatorem wariancji (w populacji)

Zadania

Zad. 1. (n nieparzyste) Badając nieśność kur Leghorn w fermie, w ciągu miesiąca uzyskano następujące obserwacje.

26, 25, 24, 28, 22, 26, 24, 25, 25, 27, 23, 24, 28, 21, 22, 25, 23, 22, 24, 26, 22.

Wyznaczyć średnią, medianę, modę, kwartyle, rozstęp, średnie odchylenie kwadratowe, odchylenie standardowe, współczynnik zmienności.

Zad. 2. (n parzyste) Badając nieśność kur Leghorn w fermie, w ciągu miesiąca uzyskano następujące obserwacje.

26, 25, 24, 28, 22, 26, 24, 25, 25, 27, 23, 24, 28, 21, 22, 25, 23, 22, 24, 26, 22.

Wyznaczyć średnią, medianę, modę, kwartyle, rozstęp, średnie odchylenie kwadratowe, odchylenie standardowe, współczynnik zmienności.

Zad. 3.

Próba dotycząca obserwacji poziomu hemoglobiny dla 15 kaczek rasy pekin zawiera następujące pomiary (g/100ml krwi):

11,6 11,3 13,8 14,2 13,0 14,2 12,6 13,8 12,4 13,6 12,0 13,0

12,2 12,6 12,8.

Wyznaczyć miary położenia i rozproszenia.

Zad. 4.

Rzucamy dwa razy symetryczną kostką. Zmienna losowa X każdej parze (k, l) wyrzuconych oczek przyporządkowuje sumę k + l. Wyznacz zbiór wartości zmiennej losowej X i określ rozkład (wartości x_i oraz odpowiadające im p_i. Wyznacz parametry (miary) rozkładu.

Zad. 5.

Oblicz miary położenia i rozproszenia dla zmiennej losowej X mając podany, w postaci tabeli, jej rozkład:

a)

xi	-10	-4	4	5	8
pi	0,10	0,25	0,25	0,30	0,10

b)

xi	1	2	3	5	6	7
pi	0,1	0,1	0,2	?	0,1	0,1

Przed przystąpieniem do obliczeń uzupełnij brakującą wartość prawdopodobieństwa dla zmiennej losowej x₄=5

c)

xi	-5	2	6	5	6
pi	0,15	0,20	0,25	0,30	0,10

---