Równanie różniczkowe liniowe rzędu pierwszego.

Definicja

Równanie

, gdzie

nazywamy równaniem różniczkowym liniowym rzędu pierwszego. Równanie to nazywamy jednorodnym i oznaczamy RJ, jeśli
, natomiast nazywamy niejednorodnym i oznaczamy RN, jeśli
.

Aby wyznaczyć rozwiązanie RN szukamy najpierw rozwiązań odpowiadającego mu RJ:

RJ

1) funkcja
jest rozwiązaniem RJ

2) jeśli
, to otrzymujemy równanie o zmiennych rozdzielonych

Rozdzielając zmienne

całkując

, gdzie

i przekształcając otrzymujemy kolejno

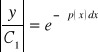
i ostatecznie

, gdzie
.

Jednakże jeśli
, to otrzymujemy wcześniej wyznaczone rozwiązanie
.

Zatem całką ogólną równania jednorodnego CORJ jest rodzina

dla
R.

Twierdzenie

Jeśli
, to
jest całką ogólną RJ, ponadto przez każdy punkt obszaru
przechodzi dokładnie jedna krzywa całkowa tego równania.

Uwaga

Całka ogólna RJ zawiera wszystkie krzywe całkowe RJ.

Aby wyznaczyć CORN (całkę ogólną równania niejednorodnego) stosujemy jedną z dwóch metod.

CORJ
CORN

I. Metoda uzmienniania stałej

Stałą C zastępujemy taką funkcją C(x), aby

było CORN. Wtedy

stąd

zatem

i

jest CORN.

Twierdzenie

Jeśli
, to

jest całką ogólną równania niejednorodnego, ponadto przez każdy punkt obszaru
R
przechodzi dokładnie jedna krzywa całkowa.

Przykład

Znaleźć całkę ogólną równania
.

Nie jest to równanie liniowe funkcji
, ale jest równaniem liniowym funkcji odwrotnej
. Zatem w przedziale w którym
mamy

RN

Szukamy najpierw rozwiązań równania jednorodnego

RJ

przekształcamy

stąd

dla

czyli

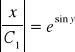
dla

i ostatecznie

dla
.

Jeśli
, to
i
spełnia RJ. Stąd otrzymujemy CORJ:

dla
R.

Uzmienniamy stałą

różniczkujemy

i podstawiając do RN otrzymujemy

czyli

.

Stąd

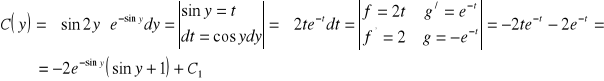
Ostatecznie

- CORN

jest również całką ogólną równania wyjściowego.

Twierdzenie

Niech
- CORJ,

- CSRN (całka szczególna równania niejednorodnego).

Wtedy

- CORN.

Dowód (szkic):

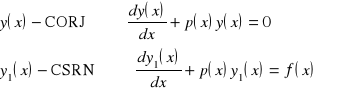
stąd widać, że

- rozwiązanie RN.

II. Metoda przewidywań

Polega na odgadnięciu CSRN, gdy dana jest CORJ, i wtedy CORN=CSRN+CORJ, na podstawie powyższego twierdzenia. Metodę stosujemy, gdy

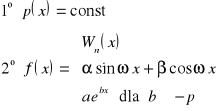
lub jest sumą lub iloczynem powyższych funkcji

Wtedy

CSRN - jest tej samej postaci co funkcja f i zachowuje odpowiednio

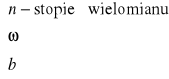
oraz przyjmuje pozostałe współczynniki stałe, które wyznaczymy z RN.

Przykład

Znaleźć całkę szczególną CSR równania
RN,

spełniającą następujący warunek
.

Szukamy rozwiązania równania jednorodnego

RJ

Stąd

dla

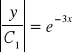
dla

i ostatecznie

.

Ponadto, jeśli

Zatem

- CORJ.

Zastosujmy metodę przewidywań.

Niech

- CSRN.

wtedy

Podstawiając do RN otrzymujemy

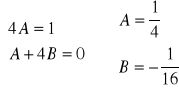
Stąd

- CSRN.

Ostatecznie

- CORN.

Teraz z rodziny CORN wybieramy tę, dla której
. Wtedy

Zatem

- CSRN spełniająca warunek początkowy
.

Twierdzenie

Niech
- całka szczególna równania
RN₁,

- całka szczególna równania
RN₂.

Wtedy

jest całką szczególną równania
RN.

Dowód (szkic):

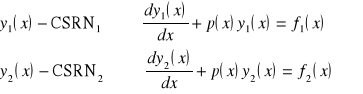
stąd widać że

- rozwiązanie równania RN.

Twierdzenie to wykorzystujemy do obliczenia całek RN w przypadku, gdy funkcja f jest kombinacją liniową wcześniej wymienionych trzech typów funkcji.

Przykład

Znaleźć całkę szczególną równania
RN

spełniającą warunek początkowy
.

Rozwiązaniem równania jednorodnego

RJ

jest

CORJ.

Wyznaczmy CS dwóch równań niejednorodnych

i

stosując metodę przewidywań.

Niech

.

Wtedy

i wstawiając do
otrzymujemy

stąd

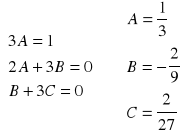
Zatem

.

Niech

.

Wtedy kolejno

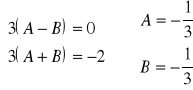
Zatem

.

Stąd otrzymujemy

- CORN

czyli

- CORN

Uwzględniając warunek początkowy

otrzymujemy

i stąd

jest CSRN spełniającą warunek początkowy
.

1

15