2. Wstęp matematyczny

Poniżej przypomniane zostaną wybrane wiadomości z matematyki mające istotne znaczenie dla posługiwania się językiem przyrody. W otaczającym nas świecie mamy głównie do czynienia z wielkościami fizycznymi posiadającymi wartość i nazywanymi skalarami oraz z wielkościami, do opisu których wymagane jest także, oprócz wartości podanie: punktu zaczepienia, kierunku oraz zwrotu i nazywanymi wektorami. Przykładami skalarów są: masa, czas, energia, moc, ładunek, potencjał, rezystancja, strumień indukcji. Do wielkości wektorowych zaliczamy np.: prędkość, przyspieszenie, pęd, siłę, natężenie i indukcję pola wektorowego.

Wektor
możemy rozłożyć na składowe we współrzędnych prostokątnych na wektory
Ostatnie składowe odpowiadają wektorom w kierunku osi x, y i z (rysunek 6). Wprowadzimy teraz wersory, czyli wektory jednostkowe w kierunkach osi x, y i z oraz oznaczymy je jak na rysunku:
Ponieważ są to wektory o wartości równej 1 możemy je zdefiniować w następujący sposób:

,
,
.

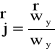
Wykorzystując powyższe równania możemy zapisać wektor
w postaci:

lub skrótowo: (w_x, w_y, w_z).

Rys.6 Rozkład wektora na składowe we współrzędnych prostokątnych

Przypomnimy teraz podstawowe działania na wektorach. Wektory możemy dodawać, odejmować, mnożyć przez liczbę oraz mnożyć wektory przez siebie (iloczyn skalarny lub wektorowy). Dodanie wektorów
i
polega na dodaniu odpowiednio ich współrzędnych. Otrzymujemy równanie:

.

Skrótowo można to zapisać za pomocą znaku sumy Σ:

.

Mnożenie wektora przez skalar polega na wymnożeniu jego wszystkich składowych przez tą samą liczbę:

.

Mnożenie wektorów przez siebie może w wyniku dawać skalar i mówimy wtedy o iloczynie skalarnym lub wektor i mówimy wtedy o iloczynie wektorowym. Iloczyn skalarny wektorów
i
to takie działanie, które tej parze wektorów przyporządkowuje liczbę (skalar) c taki, że jego wartość jest równa:

,

gdzie α jest kątem między wektorami. Ponieważ funkcja cosinus jest parzysta to iloczyn wektorowy jest przemienny:

.

Wartość jednego z wektorów pomnożona przez cosα jest równa długości rzutu tego wektora na kierunek drugiego wektora. Tak więc sens geometryczny iloczynu skalarnego jest taki, że jest to iloczyn długości jednego z wektorów i długości rzutu drugiego na kierunek pierwszego. Warto w tym miejscu zauważyć, że w przypadku wersorów iloczyn skalarny tych samych wersorów jest równy 1 a różnych 0.

dla
(cos 0 = 1),

dla
(cos 90^o=0).

We współrzędnych prostokątnych możemy iloczyn skalarny zapisać:

.

Mając wyliczony iloczyn skalarny (ze współrzędnych) i znane długości wektorów można obliczyć cosinus kąta między nimi:

.

Iloczyn wektorowy wektorów
i
to takie działanie, które tej parze wektorów przyporządkowuje wektor
taki, że:

• jego wartość jest równa: c = u·w·sinα ,

• 
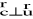
  i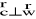
  ,

• zwrot wektora
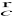
  określamy z reguły śruby prawoskrętnej,

• wektor
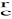
  jest funkcją kąta α.

Zauważmy, że w⋅sinα jest długością wysokości w równoległoboku wyznaczonym przez wektory
i
. Oznacza to, że wartość (długość) wektora
jest równa wartości pola powierzchni równoległoboku zbudowanego na wektorach
i
.

Mając współrzędne wektorów
i
można wyliczyć współrzędne wektora
przy pomocy wyznacznika:

=
=
.

Z własności iloczynu wektorowego wynika, że iloczyn wektorowy wektorów równoległych jest równy 0 (sin 0^o = 0). Iloczyn wektorowy nie jest też przemienny [sin(-α) = - sinα]. Stąd:

.

Aby nie zniechęcić czytelnika zostaną teraz przedstawione niektóre cechy wielkości pochodnych i pierwotnych występujących w fizyce. Łączą się one z matematycznymi pojęciami pochodnej i całki. Wielkość fizyczną (np. szybkość v - skalar) pochodną w stosunku do danej wielkości fizycznej (np. s - droga liczona w układzie toru) możemy traktować jako szybkość zmian tej drugiej w funkcji zmiennej niezależnej (np. czasu - t). Rysunek 7 przedstawia wykres zależności drogi od czasu s(t).

Rys. 7 Ilustracja interpretacji geometrycznej pochodnej funkcji

Na rysunku zaznaczono dwa punkty o współrzędnych (t₁, s₁) i (t₂, s₂) oraz odpowiadające im różnice Δs i Δt. Te ostanie dwie wartości pozwalają wyliczyć iloraz różnicowy Δs/Δt równy tangensowi α₁, czyli współczynnikowi kierunkowemu siecznej przechodzącej przez te punkty. Sens fizyczny tego ilorazu różnicowego wyraża średnią szybkość ciała. Jeśli punkt drugi będziemy przesuwać w kierunku pierwszego (t₂→t₁) to wartość ilorazu różnicowego będzie zmierzać do wartości równej tgα, czyli współczynnikowi kierunkowemu stycznej do wykresu funkcji s(t) dla t=t₁. Wielkość tą nazywamy w tym przypadku szybkością chwilową ciała w momencie t₁. Mówimy, że szybkość definiujemy jako pochodną drogi po czasie i zapisujemy:

.

Tak więc nachylenie stycznej do wykresu s(t) w punkcie t₁ jest miarą pochodnej wielkości zależnej s (funkcji s(t)) względem wielkości niezależnej t. Czyli szybkość v jest pochodną drogi s po czasie t. W drugą stronę s jest wielkością pierwotną w stosunku do v. Policzymy teraz drogę s w przedziale od t₁ do t₂. Rysunek 8 przedstawia zależność szybkości od czasu i sposób liczenia drogi.

Rys.8 Sposób liczenia drogi w przedziale od t₁ do t₂ .

Wycinamy cienki pasek powierzchni Δs tak aby można było przyjąć stałą wartość szybkości v. W tym przedziale pole powierzchni Δs będzie równe:

Δs= v Δt .

Wartość całkowitej powierzchni pod wykresem v(t) obliczymy sumując przyczynki Δs_i w przedziale od t₁ do t₂. Chcąc obliczyć dokładną wartość pola powierzchni pod krzywą v(t) musimy przeprowadzić podział na nieskończenie małe elementy ds (ds to Δs→0), a następnie przeprowadzić ich nieskończone sumowanie. Proces matematyczny odpowiadający tej procedurze nazywamy całkowaniem i zapisujemy:

.

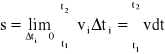
Pole powierzchni pod krzywą jest więc miarą wielkości pierwotnej (drogi) w stosunku do wielkości będącej tu zmienną zależną (szybkości).

Relacje między wielkościami pierwotnymi i pochodnymi obrazuje rysunek 9. Ukazuje on również stopniowanie tych pojęć. Zaznaczono na nim pochodną po czasie z szybkości (drugą pochodną z drogi po czasie) jaką jest przyspieszenie.

Rys. 9 Wielkości pochodne i pierwotne w fizyce

W rozdziale 3 przedstawimy podobną do szybkości, ale wektorową wielkość nazywaną prędkością. Jest ona definiowana jako pochodna wektora położenia po czasie.

,

gdzie
jest wektorem wodzącym w układzie odniesienia.

---