Uniwersytet Medyczny w Łodzi

Wydział wojskowo lekarski

zajęcia laboratoryjne z biofizyki

Piotr

Kowalski

grupa iV

zespół nr 7

Temat: KOLORYMETRYCZNE POMIARY STĘŻEŃ ROZTWORÓW

1. Szacowanie niepewności pomiarów.

Pomiary fizyczne polegają na porównywaniu wielkości mierzonej z przyjętym wzorcem czyli jednostką. Badania fizyki doświadczalnej mają na celu poszukiwanie i ustalanie związków między różnymi wielkościami fizycznymi. Doświadczenia prowadzone w laboratorium fizycznym polegają na dokonywaniu pomiarów różnych wielkości fizycznych. Wielkością fizyczną nazywa się taką cechę ciała lub zjawiska, którą da się w sposób liczbowy porównać z analogicznymi cechami innych przedmiotów lub zjawisk.

Pomiary proste (bezpośrednie) dokonywane są bezpośrednio za pomocą przyrządów pomiarowych np. pomiar długości wykonany suwmiarką, pomiar masy ciała za pomocą wagi, pomiar czasu za pomocą stopera itp.

Pomiary złożone (pośrednie) polegają na wyznaczaniu wartości wielkości złożonej na podstawie znanych zależności między różnymi wielkościami mierzonymi bezpośrednio np. pomiar oporności elektrycznej metodą techniczną na podstawie zmierzonych bezpośrednio wartości natężenia i napięcia albo wyznaczanie przyśpieszenia ziemskiego za pomocą wahadła matematycznego na podstawie pomiaru długości wahadła i jego okresu drgań.

Każdy pomiar jest wykonywany z określoną dokładnością, dlatego wyniki otrzymywane z pomiarów nie wyrażają w sposób absolutny tej wartości, lecz stanowią tylko przybliżenie wartości rzeczywistej. Inaczej mówiąc każdy pomiar obarczony jest pewnym błędem, który może wynikać z : niedoskonałości stosowanych przyrządów pomiarowych, ograniczonych zdolności zmysłów eksperymentatora, zmiany warunków zewnętrznych występujące podczas prowadzenia pomiarów. Dlatego ważnym problemem praktycznym jest ocena wiarygodności otrzymanych wyników pomiarowych oraz oszacowanie lub obliczenie niepewności wyniku pomiaru, który służy do określenia stopnia zaufania do otrzymanego rezultatu.

Niepewność pomiaru jest miarą rozrzutu wyników powtarzanych pomiarów danej wielkości fizycznej. Zapisując wynik pomiaru fizycznego x należy wyraźnie zaznaczyć jednostkę podanej wartości i opatrzyć przedziałem niepewności ၄x:

x Ⴑ ၄x

np. zmierzona mikrometrem średnica drutu d wynosi d = (2,53 Ⴑ 0,01) mm.

2. Typy błędów pomiarowych:

Błędy systematyczne- wynikają z wadliwego działania przyrządu pomiarowego (np. przesunięcie zera skali, spieszący się stoper, zużycie części elementów) lub ze źle zaprojektowanego doświadczenia (np. waga jest ustawiona blisko grzejnika i jedno ramię jej belki jest dłuższe od drugiego). Cechą charakterystyczną tych błędów jest to, że wykazują jednokierunkowość, tzn. są albo stale za małe, albo stale za duże. Błędy systematyczne można eliminować przez kalibrację przyrządów lub takie projektowanie układów pomiarowych aby błędy te nie występowały.

Błędy przypadkowe- wynikają z ograniczonej ostrości zmysłu obserwatora lub z mało widocznych zmian środowiska pomiarowych. Powtarzanie pomiaru wielkości fizycznej daje różne wyniki. Otrzymane wartości (wyniki) rozkładają się wokół wartości rzeczywistej a ich rozrzut zależy od dokładności prowadzonych pomiarów. Cechą charakterystyczną tych błędów jest ich dwukierunkowość, polegająca na tym, że w serii pomiarów wyniki z nadmiarem i niedomiarem występują z tą samą częstotliwością, Niepewności przypadkowe można zmniejszyć stosując dokładniejsze przyrządy i dbając o zapewnienie niezmiennych warunków doświadczenia - nie można ich jednak całkowicie uniknąć.

Błędy grube- powstają wskutek fałszywego odczytu przyrządu lub ewidentnej pomyłki eksperymentatora np. zapisanie wyniku pomiaru długości w centymetrach zamiast w milimetrach. Pomiar obarczony błędem grubym jest łatwy do identyfikacji ze względu na duże wartości. Powtarzanie pomiarów pozwala zatem dostrzec i wyeliminować (odrzucić) wyniki obarczone błędem grubym.

Błąd bezwzględny- mierzony jako różnica między wartością rzeczywistą wielkości X_o a wartością przybliżoną otrzymaną z pomiaru X_i nazywa się rzeczywistym.

ΔX = X_i - X

W związku z tym, że najczęściej wartość rzeczywista nie jest znana, błąd bezwzględny odnosi się do średniej arytmetycznej.

_{gdzie: n- całkowita liczba wykonanych pomiarów}

Błąd względny- stosunek błędu bezwzględnego do prawdziwej wartości wielkości mierzonej i jest bardziej miarodajny od błędu bezwzględnego:

b=

Błąd względny procentowy : bp=
* 100%

3. Szereg statystyczny, wariancja i odchylenie standardowe.

Szereg statystyczny - zebrany w wyniku prowadzonego badania statystycznego materiał statystyczny poddawany analizie, ktora jest prowadzona na kilku poziomach, wśród których wyróżniamy czynności obejmujące:
a) grupowanie, systematyzowanie i klasyfikowanie według zadanych klas, przedziałów, typów, grup, itp.,
b) wizualizację graficzną danych pierwotnych lub wtórnych otrzymanych w wyniku realizacji punktu a),
c) obliczenia numeryczne wybranych wielkości z próby,
d) interpretację empiryczną uwzględniającą wszystkie podpunkty a), b) i c) .

Wariancją z próby nazywamy średnią arytmetyczną kwadratów różnic pomiędzy wynikami badanej cechy a ich średnią z próby.

Odchylenie standardowe:

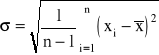
jest miarą niepewności pojedynczego wyniku pomiaru.

4. Rozkład normalny i rozkład Studenta.

Wielokrotne niezależne powtarzanie tego samego pomiaru fizycznego pozwala otrzymać serię wyników x_1, x_2, x₃ ...... x_n gdzie n - liczba wykonanych pomiarów. Rzeczywistej wartości wielkości fizycznej nie znamy ale można wykazać, że najbardziej zbliżona do niej jest średnia arytmetyczna otrzymanych wyników
_.

Wyniki pomiarów układają się wokół wartości średniej arytmetycznej. Przy bardzo dużej liczbie pomiarów (
) rozkład ten może być opisany funkcją

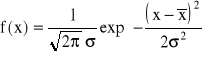
zwaną rozkładem normalnym (Gaussa)

f(x) - gęstość prawdopodobieństwa

- odchylenie standardowe

Rozkład prawdopodobieństwa Gaussa daje możliwość obliczenia prawdopodobieństwa, że dowolny wynik pomiaru znajduje się w zadanym przedziale wartości x.

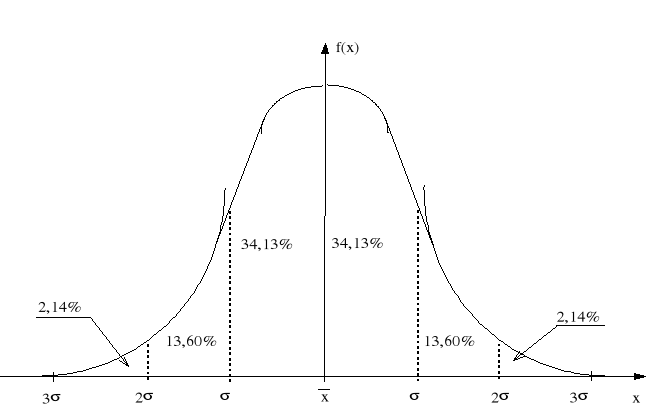
Rys 1. Krzywa Gaussa rozkładu niepewności przypadkowych. Wartości liczbowe określają procentowe prawdopodobieństwa pojawienia się wyniku pomiaru w wyznaczonych przedziałach.

Rozkład Studenta - stosowany jest w przypadku, gdy seria pomiarowa złożona jest z niewielkiej liczby pomiarów (n < 5) jako miarę niepewności średniej arytmetycznej przyjmuje się połowę tzw. przedziału ufności czyli wielkość
. Odchylenie standardowe mnożymy przez pewien współczynnik t(n, p) (współczynnik Studenta) zależny od liczby pomiarów n i zadanego prawdopodobieństwa p. Przedział
nazywa się przedziałem ufności.

Prawdopodobieństwo, że przedział ufności obejmuje wartość rzeczywistą mierzonej wielkości nosi nazwę poziomu ufności.

5. Analiza korelacji i regresji.

Współczynnik korelacji r stanowi informację o współzależności miedzy dwiema zmiennymi i może przyjmować wartości od -1 do 1. Kiedy r=0, brak jest związku między cechami, a gdy r=1 związek ma charakter funkcyjny. Gdy znak r<0, mamy korelację ujemną (wzrostowi zmiennej x towarzyszy spadek zmiennej)

Na podstawie współczynnika korelacji można określić związek korelacyjny między cechami, którego wykresem jest regresja prostoliniowa o równaniu y=ax+b. Równanie to pozwala oszacować wartość cechy zależnej y na podstawie cechy niezależnej x.

O korelacji mówimy, wtedy jeżeli średnim wartościom jednej cechy ściśle odpowiadają wartości drugiej cechy (funkcja - każdej wartości x odpowiada tylko jedna wartość y).

---