Wstęp teoretyczny
Pryzmatem optycznym nazywamy ośrodek załamujący światło, ograniczony nierównoległymi płaszczyznami. Linia przecięcia obu płaszczyzn nosi nazwę krawędzi łamiącej, a kąt przestrzenny zawarty między płaszczyznami - kąta łamiącego pryzmatu. Przekrój pryzmatu prostopadły do krawędzi łamiącej nazywamy przekrojem głównym. Pryzmaty ze szkła lub substancji stałej szlifowanej są w postaci graniastosłupów trójkątnych, o przekroju głównym w postaci trójkąta. Jeżeli smukła wiązka światła białego pada na pryzmat po kątem α, to ulega ona rozszczepieniu na barwną smugę, zwaną widmem, którą cechują różne kąty załamania dla różnych barw światła.
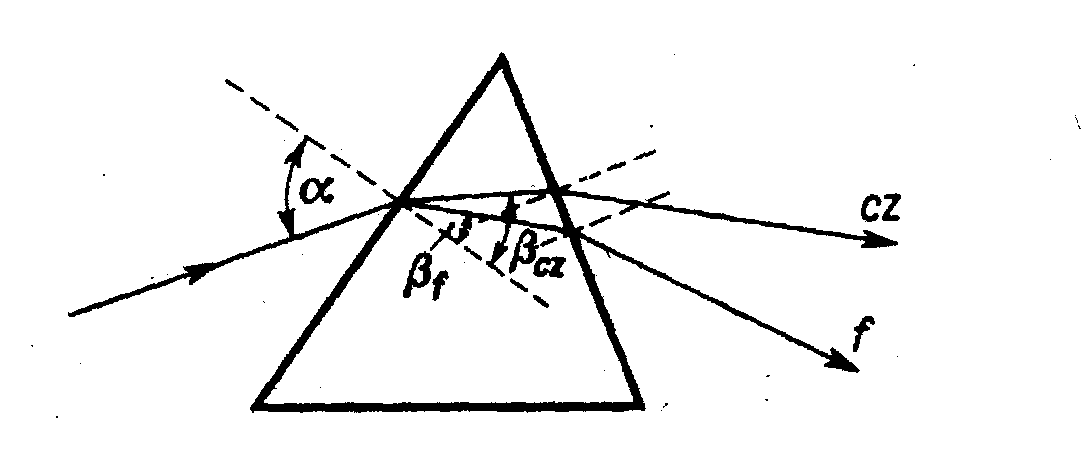
Ponieważ kąt padania α dla wszystkich barw zawartych w świetle białym jest ten sam, a kąty załamania β są różne, wobec tego współczynnik załamania
![]()
dla różnych barw jest różny.
Dla każdej substancji współczynniki załamania różnych barw mają określone wartości.
Promień światła jednobarwnego padający na pryzmat pod kątem α1 ulega dwukrotnie załamaniu i wychodzi z niego, doznając odchylenia którego miarą jest kąt δ
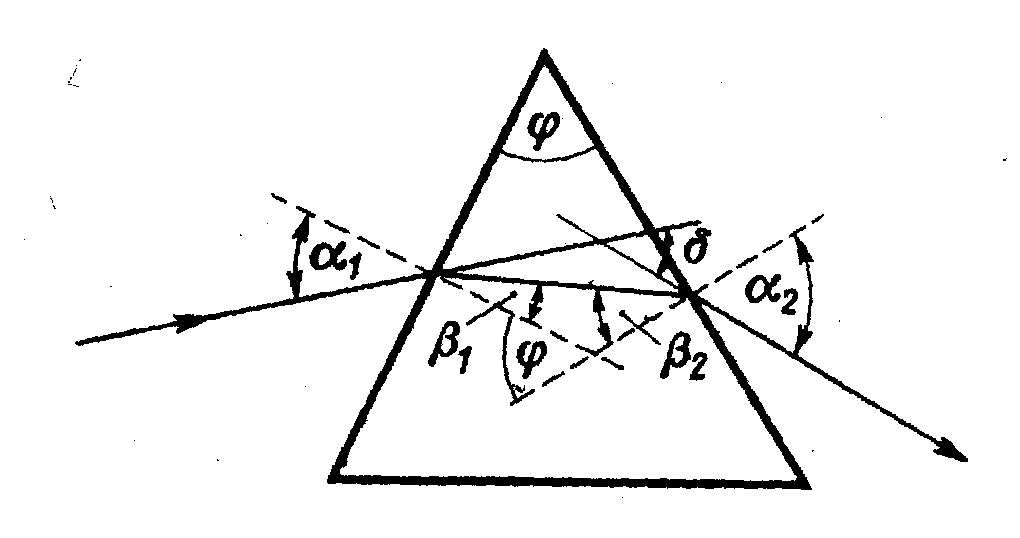
Z konstrukcji geometrycznej przedstawiającej bieg promienia wynika, że
δ=α1-β1+α2-β2,
lub inaczej
δ=α1+α2-(β1+β2);
ale β1+β2=ϕ więc
δ=α1+α2-ϕ.
Kąt odchylenia δ zależy od kąta padania α1, od współczynnika załamania pryzmatu n (α2 zależy od n) i od kąta łamiącego ϕ . Kąt odchylenia osiąga minimum, gdy bieg promieni jest symetryczny w stosunku do pryzmatu, tzn. gdy wewnątrz pryzmatu promień jest prostopadły do dwusiecznej kąta łamiącego. Wówczas α1=α2=α oraz β1=β2=β więc możemy napisać:
δmin=2α-ϕ
Z równania tego wyznaczamy kąt α
![]()
Biorąc pod uwagę β otrzymujemy
β=ϕ/2
Podstawiając znalezione wartości α i β do wzoru definiującego współczynnik załamania
![]()
Otrzymujemy na n wzór następujący:
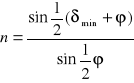
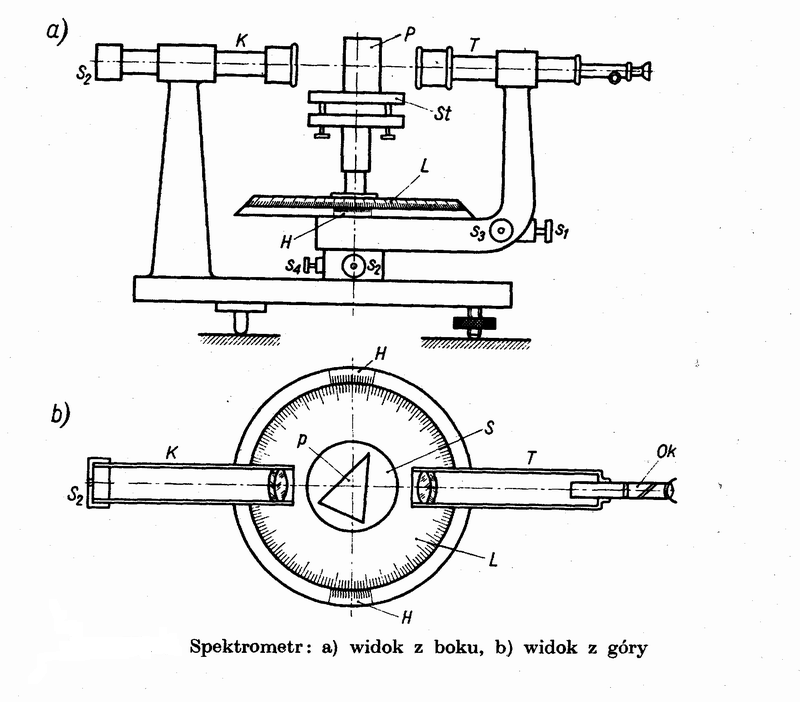
Mierząc kąt łamiący pryzmatu ϕ oraz kąt minimum odchylenia δmin możemy wyznaczyć współczynnik załamania substancji, z której wykonany jest pryzmat. Pomiar obu kątów przeprowadzamy przy pomocy spektrometru.
![]()
![]()
![]()
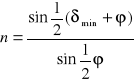
Wyszukiwarka