ADDYTYWNY, LINIOWY MODEL TENDENCJI ROZWOJOWEJ BEZ UWZGLĘDNIANIA
WAHAŃ OKRESOWYCH
Założenia
- model tendencji rozwojowej budujemy na podstawie szeregu czasowego ![]()
, gdy elementy ![]()
nie zawierają wahań okresowych,
- wahania przypadkowe nakładają się na trend zjawiska w sposób addytywny.
Ogólna postać modelu
![]()
; ![]()
gdzie:
![]()
- funkcja trendu opisująca tendencję rozwojową badanego zjawiska, ![]()
![]()
- zmienna losowa reprezentującą wahania przypadkowe.
Postać liniowego modelu tendencji rozwojowej
![]()
; ![]()
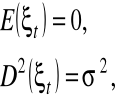
![]()
dla ![]()
Przykład
Lata
|
|
|
|
|
|
1993 |
0 |
175 |
0 |
0 |
180,1 |
1994 |
1 |
248 |
248 |
1 |
235,7 |
1995 |
2 |
288 |
576 |
4 |
291,4 |
1996 |
3 |
343 |
1029 |
9 |
347,0 |
1997 |
4 |
397 |
1588 |
16 |
402,6 |
1998 |
5 |
464 |
2320 |
25 |
458,2 |
|
15 |
1915 |
5761 |
55 |
1915 |
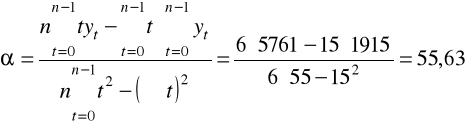
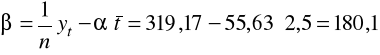
![]()
ADDYTYWNY, LINIOWY MODEL TENDENCJI ROZWOJOWEJ PRZY UWZGLĘDNIENIU
WAHAŃ OKRESOWYCH
Założenia
- model tendencji rozwojowej budujemy na podstawie szeregu czasowego ![]()
, gdy elementy ![]()
zawierają wahania okresowe,
- wahania przypadkowe nakładają się na trend zjawiska w sposób addytywny.
Postać modelu
![]()
![]()
,
gdzie ![]()
są zmiennymi zero-jedynkowymi reprezentującymi poszczególne podokresy cyklu:
1, dla obserwacji dotyczących i-tego kwartału,
![]()
0, dla obserwacji dotyczących pozostałych kwartałów.
![]()
,
![]()
,
![]()
dla ![]()
,
![]()
.
Parametry ![]()
stojące przy zmiennych zero-jedynkowych charakteryzują absolutną wielkość wahań okresowych w poszczególnych kwartałach.
Uwarunkowania
pomiędzy zmiennymi niezależnymi modelu zachodzi zależność liniowa postaci
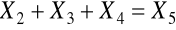
eliminujemy z modelu dowolną zmienną zero-jedynkową, zastępując ją przez kombinację liniową pozostałych zmiennych
parametry dla reprezentowanych w modelu wariantów zmiennej jakościowej mierzą wpływ tych wariantów odniesiony do wpływu wariantów pominiętego
wyraz wolny jest powiększony o wartość mierzącą wpływ pominiętego wariantu cechy jakościowej
ANALIZA WAHAŃ PRZYPADKOWYCH
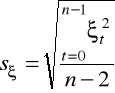
gdzie:
![]()
Wartość odchylenia standardowego reszt mówi, o ile średnio wartości zjawiska obserwowane w poszczególnych okresach odchylają się od wartości teoretycznych tego zjawiska na skutek wahań przypadkowych.
Przykład
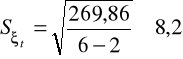
WERYFIKACJA MODELU. TEST DURBINA - WATSONA
Autokorelacja składnika losowego
przyczyna: w szeregu czasowym występuje przeważnie wtedy gdy efekt oddziaływania czynników przypadkowych trwa dłużej niż jednostka czasu przyjęta w badaniu,
pomiar: współczynnik autokorelacji rzędu 1 (odległość pomiędzy składnikami losowymi wynosi jednostkę):
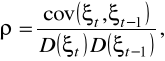
którego nieobciążonym estymatorem jest współczynnik autokorelacji reszt modelu:
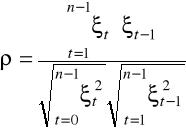
Weryfikacja hipotezy dotyczącej
skorelowania składników losowych
1. Stawiamy hipotezę, że sąsiadujące ze sobą składniki losowe w addytywnym modelu tendencji rozwojowej są nieskorelowane:
![]()
wobec hipotezy alternatywnej:
![]()
2. Jeżeli ![]()
jest prawdziwa, to statystyka d o postaci:
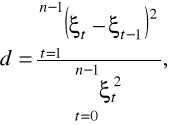
posiada rozkład Durbina - Watsona, który zależy od liczby obserwacji (n) oraz liczby zmiennych niezależnych w modelu (m).
Pomiędzy statystyką d a współczynnikiem autokorelacji z próby ![]()
zachodzi zależność:
![]()
z czego wynika, że ![]()
przy czym
jeżeli ![]()
to ![]()
.
3. Przy danym poziomie istotności 2 ustalamy wartości krytyczne statystyki d oznaczane jako ![]()
i ![]()
, wyznaczające obszary podejmowania decyzji odnośnie sprawdzanej ![]()
:
![]()
odrzucamy,
![]()
nie podejmujemy żadnej decyzji,
![]()
przyjmujemy.
odrzucamy brak przyjmujemy brak odrzucamy
H0 decyzji H0 decyzji H0
0 d1 d2 2 d3 d4 4
(4-d2) (4-d1)
Przykład
![]()
![]()
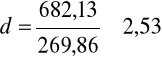
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
PROGNOZA NA PODSTAWIE ADDYTYWNEGO MODELU WAHAŃ W CZASIE Z LINIOWĄ FUNKCJĄ TRENDU
dokonujemy prognozy, opierając się na klasycznym modelu trendu liniowego:
![]()
gdzie:
T=n-1+w - jest okresem prognozowanym,
przy czym:
w - długość prognozy.
estymator średniego błędu prognozy określamy jako:
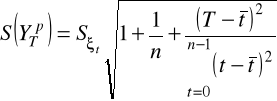
uwzględnienie wahań okresowych
addytywne wahania okresowe:
![]()
.
multiplikatywne wahania okresowe:
![]()
.
Przykład
Dokonujemy prognozy liczby złamań w 2002 roku
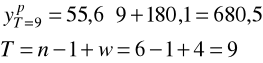
Błąd prognozy
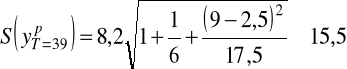
Wyszukiwarka