Cel ćwiczenia
Celem ćwiczenia jest zaobserwowanie zachowania się cieczy w naczyniu cylindrycznym wirującym wokół osi pionowej, oraz teoretyczne i doświadczalne wyznaczanie kształtu swobodnej powierzchni cieczy.
Podstawy teoretyczne
Ciecz jest w równowadze względnej wówczas, gdy pozostaje ona w stanie spoczynku względem ścian poruszającego się naczynia. Występuje to wtedy, gdy naczynie porusza się ruchem jednostajnym, jednostajnie przyspieszonym prostoliniowym bądź ruchem jednostajnie obrotowym wokół osi pionowej. Efektem wizualnym równowagi względnej jest ukształtowanie swobodnej powierzchni cieczy. W naczyniu cylindrycznym ma ona kształt paraboloidy obrotowej, o osi pokrywającej się z osią obrotu naczynia.
Równanie opisujące kształt swobodnej powierzchni cieczy w naczyniu o promieniu R = ![]()
, wypełnionym do wysokości h cieczą i wirującym z prędkością kątową ω jest następujące
![]()
Rysunek i opis stanowiska pomiarowego
Przyrządy użyte przy wykonywaniu ćwiczenia:
- naczynie cylindryczne N, wypełnione wodą, obracające się wokół własnej osi
- urządzenia do regulacji i pomiaru prędkości obrotowej naczynia.
- wodowskaz szpilkowy odgórny G
- stoper
Wyniki pomiarów w protokole.
Obliczenia wg wzorów .
![]()
![]()
1. Doświadczenie pierwsze.
![]()
2. Doświadczenie drugie.
![]()
Wyznaczenie równania paraboloidy obrotowej
Przyrost ciśnienia:
1. Doświadczenie pierwsze.
![]()
dla powierzchni o stałym ciśnieniu równanie ![]()
przyjmuje rozwiązanie :
![]()
dla warunków r = 0; z = z0
![]()
po przekształceniu ![]()
Równanie powierzchni swobodnej:
![]()
(1)
Zakładając, że r = R; z = h, gdzie R jest promieniem naczynia cylindrycznego, h wysokość napełnienia, otrzymujemy:
![]()
(2)
zb - wierzchołek paraboloidy obrotowej
H - wysokość wzniesienia zwierciadła wody w ruchu obrotowym
![]()
Po połączeniu wzorów (1) i(2), otrzymujemy równanie teoretyczne opisujące kształt swobodnej powierzchni cieczy w naczyniu:
![]()
![]()
Obliczenie i narysowanie paraboloidy empirycznej i teoretycznej
1.Doświadczenie pierwsze.
h = 14,7 cm
w1 = 3,77 1/s
R = 48,75 cm
g = 9,81 m/s2
![]()
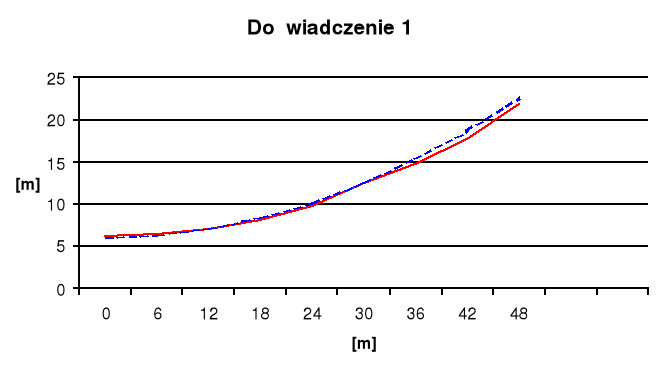
- - - - - - - krzywa teoretyczna
----------- krzywa rzeczywista
2. Doświadczenie drugie.
h = 14,7cm
w2 =1,82 [1/s]
R = 48,75 cm
g = 9,81 m/s2
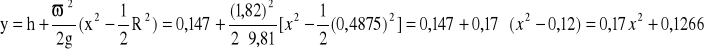
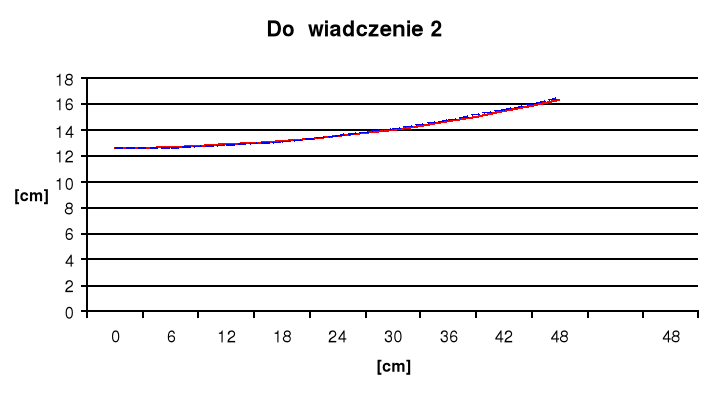
- - - - - - - krzywa teoretyczna
----------- krzywa rzeczywista
Rachunek błędów
![]()
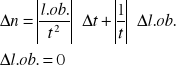
Obliczenie błędu względnego Δt dla pomiaru 1 .
l.p. |
t [s] |
Δt [s] |
1 |
25,1 |
0,033 |
2 |
25,1 |
0,033 |
3 |
25,1 |
0,033 |
4 |
25,0 |
0,067 |
5 |
25,1 |
0,033 |
6 |
25,0 |
0,067 |
x |
25,067 |
0,044 |
![]()
Δn =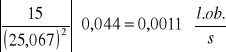
ω=2πn czyli Δω=2πΔn = 0,0069 [1/s]
ω=3,77 ± 0,0069 [1/s]
Obliczenie błędów względnych Δt dla pomiaru 2 .
l.p. |
t [s] |
Δt [s] |
1 |
34,1 |
0,050 |
2 |
34,1 |
0,050 |
3 |
34,2 |
0,050 |
4 |
34,2 |
0,050 |
5 |
34,2 |
0,050 |
6 |
34,1 |
0,050 |
x |
34,150 |
0,050 |
![]()
Δn =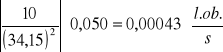
ω=2πn czyli Δω=2πΔn = 0,0027 [1/s]
ω=1,82 ± 0,0027 [1/s]
Dyskusja błędów
Punkty paraboli obliczone wg równania teoretycznego dla pomiaru 1 obarczone są błędem ±0,0069 1/s, wynikającym z pomiaru prędkości kątowej. Natomiast wartości empiryczne obarczone są błędem pomiaru wodowskazem ± 0,01cm. Wartości te nieznacznie różnią się między sobą. W doświadczeniu drugim błąd prędkości kątowej jest mniejszy niż w doświadczeniu pierwszym, wynosi ± 0,0027 1/s, zatem wartości z doświadczenia drugiego obarczone są mniejszym błędem. Różnica między teoretycznym a empirycznym punktem paraboli jest dużo mniejsza niż w doświadczeniu pierwszym.
Wnioski
Wartość w środku wirującego naczynia, czyli wierzchołek paraboli w doświadczeniu1 różni się od wartości w doświadczeniu 2 o 6,4cm, a wartości przy ściankach naczynia o 5,4 cm. Można tez zauważyć, że w doświadczeniu 1 przy większej prędkości kątowej różnica pomiędzy wierzchołkiem paraboli, a punktem stycznym do zbiornika wynosi 15,6 cm, a w doświadczeniu 2 tylko 3,8 cm. Z tego wynika że, przy małej prędkości kątowej paraboloida jest prawie pozioma, a przy dużej mocno wklęsła.
Wyszukiwarka