INZYNIERII I TECHNOLOGII CHEMICZNEJ |
KRZYSZTOF BARANOWSKI |
ZESPÓŁ:
3 |
OCENA: |
GRUPA:
11 |
Wyznaczanie przyśpieszenia ziemskiego za pomocą wahadła matematycznego |
NR. ĆWICZENIA:
1 |
DATA WYKONANIA: 19.02.2003 |
CZĘŚĆ TEORETYCZNA:
NIEPEWNOŚĆ POMIAROWA - jest to połowa szerokości przedziału w którym znajduje się wartość rzeczywista . Wyróżniamy niepewności przypadkowe wynikające z przypadkowego charakteru pomiaru i niepewności systematyczne wynikające ze skończonej dokładności przyrządów.
BŁĄD POMIARU - jest to błąd wynikający z używania niesprawnych przyrządów, niewłaściwego używania lub z niepoprawnej metody pomiaru. Wyróżniamy błędy :
grube (pomyłki wynikające z błędnego odczytu wskaźnika)
systematyczne (niedokładne wykonanie przyrządów)
przypadkowe (zmienna losowa - wielkość, która w sposób przypadkowy przyjmuje wartość z pewnego przedziału liczbowego)
Miarą niepewności przypadkowej bezpośredniego pomiaru xi jest odchylenie standardowe bezpośredniego pomiaru zdefiniowanego następująco:
Sx =
Niepewność systematyczna nie ma charakteru losowego i w jednakowym stopniu wpływa na każdy wynik w serii pomiarów. Na niepewność systematyczną wpływ ma zarówno przyrząd, jak i obserwator. Niepewność przyrządu składa się z:
Δd x - niepewności wynikającej ze skończonego odstepu podziałki i jest równa połowie najmniejszej działki przyrządu.
Δk x - niepewność wzorcowania fabrycznego przyrządu i jest równa :
Δk x = kZ/100
k -klasa przyrządu
Z - jego zakres
Na niepewność systematyczną obserwatora składają się :
Δ0 x - szerokość wskazówki miernika wyrażona w jednostkach skali
Δe x - szerokość obszaru drgań wskazówki wyrazona w jednostkach skali.
Tak więc maksymalna niepewność systematyczna jest równa :
Δxs = Δd x +Δk x + Δ0 x + Δe x
Niepewność pomiarowa wielkości y = f(x1,x2,...xn) jest równa :
δ=
gdzie oznacza pochodną cząstkową funkcji y = f(x1,x2,...xn) w punkcie x=(x1,x2,...xn)
Niepewność maksymalna jest to wyrazenie postaci
Niepewność względna δw jest to miara dokładności metody pomiaru zdefiniowana jako stosunek niepewności pomiarowej
CZĘŚĆ PRAKTYCZNA :
Wykonanie ćwiczenia:
Zawieszono metalową kulkę na cienkiej, nierozciągliwej nitce o długości określonej
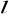
. Następnie dokonano pomiaru długości nici od punktu zawieszenia do powierzchni kulki użyto do tego metra. Średnicę kulki zmierzono za pomocą suwmiarki.
L.p |
|
|
|
cm |
cm |
1 |
61,5 |
2,89 |
2 |
60,9 |
2,87 |
3 |
60,8 |
2,88 |
4 |
61,2 |
2,88 |
5 |
61,0 |
2,89 |
|
|
|
|
||
![]()
= ![]()
[cm]
![]()
= ![]()
[cm] ![]()
[cm]
![]()
= ![]()
+ ![]()
![]()
= 61,08 cm + 1,437 cm = 62,517 [cm] = 0,62517 [m]
L.p |
|
|
|
cm |
cm |
1 |
-0,42 |
0,1764 |
2 |
0,18 |
0,0324 |
3 |
0,28 |
0,0784 |
4 |
-0,12 |
0,0144 |
5 |
0,08 |
0,0064 |
|
∑ = 0,308 |
|
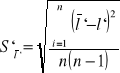
![]()
[cm] = 0,124[cm]=0,00124[m]
ΔS![]()
- niepewność systematyczna długości nici = 0,02 cm = 0,0002 m
ΔS![]()
- niepewność systematyczna pomiaru średnicy kulki = 0,02 cm = 0,0002 m
Δ![]()
max = ΔS![]()
+ 3Δ![]()
⋅ ![]()
α,n
Δ![]()
max = 0,002m + 3⋅0,00124m ⋅ 1,20 = 0,0064[m]
L.p |
|
|
|
cm |
cm |
1 |
-0,016 |
0,000256 |
2 |
0,004 |
0,000016 |
3 |
-0,006 |
0,000036 |
4 |
0,034 |
0,001156 |
5 |
-0,016 |
0,000256 |
|
∑ = 0,00172 |
|
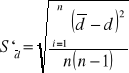
![]()
[cm] = 0,0092[cm] = 0,000092[m]
Δ![]()
max = Δ![]()
S + 3⋅![]()
+ ![]()
α,n
Δ![]()
max = 0,002m + 3⋅0,000092m ⋅ 1,20 = 0,0023[m] = Δr
Δ![]()
= Δ![]()
max + Δr = 0,0064m + 0,0023m = 0,0087[m]
Δ![]()
max ≈ Δds
d = ![]()
± Δ![]()
max = 2,874m ± 0,0023m
Δ![]()
max = Δ![]()
max + Δ![]()
max
Δ![]()
max = 0,0064m + 0,0023m = 0,0087m
Wychylono kulkę z położenia równowagi, pamiętają aby wychylenie kątowe nie było większe niż 5°. Przy pomocy stopera zmierzono czas trwania 20 okresów. Jako jeden okres rozumiemy powrót kulki do jednego ze skrajnych położeń. Pomiar powtórzono 12- krotnie , a wynik zapisano w tabeli :
L.p |
|
T = |
T - |
|
|
s |
s |
s |
s |
1 |
34,2 |
1,71 |
0,085 |
0,0072 |
2 |
34,4 |
1,72 |
0,095 |
0,0090 |
3 |
34,1 |
1,705 |
0,08 |
0,0064 |
4 |
34,0 |
1,7 |
0,075 |
0,0056 |
5 |
34,0 |
1,7 |
0,075 |
0,0056 |
6 |
33,2 |
1,66 |
0,035 |
0,0012 |
7 |
31,1 |
1,555 |
-0,07 |
0,0049 |
8 |
30,6 |
1,53 |
-0,095 |
0,0090 |
9 |
30,4 |
1,52 |
-0,105 |
0,0110 |
10 |
31,2 |
1,56 |
-0,065 |
0,0042 |
11 |
31,4 |
1,57 |
-0,055 |
0,0030 |
12 |
31,4 |
1,57 |
-0,055 |
0,0030 |
|
20 |
|
|
∑=0,0701 |
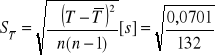
[s]= 0,023[s]
ΔTS = ![]()
[s] = 0,01[s]
ΔTmax = ΔTS + 3![]()
= 0,01[s] + 3 ⋅ 0,023[s] = 0,079[s]
Dane do obliczeń:
T = (1,625 ± 0,079)s
![]()
= (0,6251 ± 0,0064)m
g = ![]()
g = 4 ⋅ (3,14)2 ⋅ ![]()
![]()
= 4 ⋅ 9,869 ⋅ ![]()
![]()
= 9,346 ![]()
Maksymalny błąd wyznaczania przyśpieszenia ziemskiego doświadczalnie wyraża się wzorem
Δgmax = ![]()
Δgmax = ![]()
ΔT = 0,079s Δ![]()
= 0,0087m
T= 1,625s ![]()
= 0,625m
Δgmax = ![]()
Wartość przyspieszenia ziemskiego wyznaczona przy pomocy wahadła matematycznego wynosi:
g = 9,346 ± 1,03 ![]()
względny błąd maksymalny wyznaczenia g wynosi
![]()
= 0,11
błąd procentowy
![]()
⋅ 100% = 11%
Na błąd wyniku z obliczeń wpływ mogą mieć:
niedokładność pomiaru czasu, długości nici
niedokładność przyrządów użytych podczas pomiaru
różny czas reakcji oka ludzkiego.
Wyszukiwarka