Politechnika Radomska Wydział Transportu		LABORATORIUM MIERNICTWA			Data:
Imię i Nazwisko:			Grupa:	Zespół
Nr ćwiczenia:	Temat: Pomiary oscyloskopowe.				Ocena i podpis:

Cel ćwiczenia:

Celem ćwiczenia jest poznanie budowy, zasady działania i obsługi oscyloskopu elektronicznego oraz obserwacja przebiegów jednokrotnych oraz innych przebiegów na ekranie oscyloskopu, a także zapoznanie się z możliwością wykonywania za pomocą oscyloskopu pomiarów takich wielkości fizycznych, jak okres badanego przebiegu, częstotliwość, kąt przesunięcia fazowego.

1. Pomiar częstości i kąta przesunięcia fazowego za pomocą krzywych Lissajous.

Określenie amplitudy A:

A = K ⋅ L

K - stała kalibratora wejścia Y (podana w [V/cm],

L - amplituda analizowanego przebiegu [cm].

Określenie okresu T:

T = l ⋅ μ

l - długość okresu [cm],

μ - wartość podstawy czasu.

Określanie częstotliwości f:

f = 1 / T

Lp.	Amplituda A [V]	Częstotliwość f [Hz]	Okres T [s]	Uwagi
1a	0,7	68960	1,45*10^-5	Sinusoida (f=70kHz)
1b	0,7	6896,5	1,45*10^-4	Sinusoida (f=7kHz)
2a	1,615	21050	4,75*10^-5	Piła (f=20kHz)
2b	1,615	10000	1*10^-4	Piła (f=10kHz)
3a	1,6	31250	3,2*10^-5	Prostokąt (f=30kHz)
3b	1,6	3076,9	3,25*10^-4	Prostokąt (f=3kHz)

2. Pomiar przesunięcia fazowego.

Schemat ideowy:

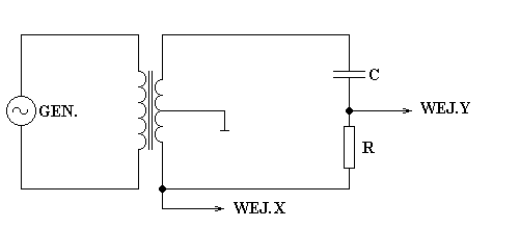
Wzory:

ϕ_obl = 180  arcsin(x_o/x)

ϕ  *ϕ_obl  ϕ*

δϕ 
100%

Przykładowe obliczenia (dla pierwszego pomiaru):

x_o/x = 0,72937

arcsin(x_o/x) = 0,8174

ϕ_obl = 180 - 0,8174 = 179,182

ϕ  *,  , *  ,

δϕ  ( 179,182  ,  ⋅ 100 % = 0,2276 %

Lp.	R []	ϕ [*	xo/x	arcsin(xo/x)	ϕobl [*	ϕ [*	δϕ 
1	20000	138,4	0,221/0,303	0,8174	179,182	40,782	0,2276
2	15000	127,4	0,236/0,265	1,0985	178,901	51,501	0,2878
3	25000	146,3	0,159/0,254	0,6763	179,323	33,023	0,1841
4	10000	110,7	0,250/0,256	1,3538	178,646	67,946	0,3803
5	50000	163,4	0,074/0,262	0,2863	179,713	16,313	0,0907
6	70000	167,4	0,045/0,257	0,1760	179,823	12,423	0,0690

3. Obserwacja przebiegów jednokrotnych.

Schemat ideowy:

Wzory:

δf = 100%

L = 4,51 [mH]

C = 3,53 [nF]

Q - dobroć układu,

N - ilość okresów do momentu, kiedy wartość amplitudy sygnału zmniejszy się do wartości równej 1/e wartości amplitudy maksymalnej sygnału.

Przykładowe obliczenia (dla pierwszego pomiaru):

[Hz]

[Hz]

1) A = 0,9

: a = 0,66 → N = 10

2) A = 0,7

: 0,5 = 0,52 → N = 9

3) A = 0,625

: 0,5 = 0,46 → N = 5

Q = 3.14... ⋅ 10 = 31,41592

δf =
100 % = 16,47 %

Lp.	R []	T [s]	f [Hz]	fobl [Hz]	f [Hz]	δf [%]	Q
1	64000	3*10^-5	33333,33	39908,43	6575,10	16,47	31,41592
2	40000	3*10^-5	33333,33	39908,43	6575,10	16,47	28,27433
3	20000	3,2*10^-5	31250	39908,43	8658,43	21,69	15,70796

Wnioski i spostrzeżenia

W ćwiczeniu korzystaliśmy z oscyloskopu na którym wyświetlane były krzywe Lissajous .

W pierwszej części powyższego ćwiczenia należało dokonać amplitudy, okresu oraz częstotliwości badanego przebiegu. Wartości te uzyskaliśmy na podstawie poniższych wzorów:

A = K * L

T = l *μ

f = 1 / T=1 / l * μ

Uzyskane wyniki są obarczone błędem. Jest on spowodowany niemożliwością dokładnego odczytania wartości indukcyjności oraz l z ekranu oscyloskopu.

Pomiar kąta przesunięcia fazowego między dwoma badanymi przebiegami wykonaliśmy przy pomocy kursorów oraz wzorów:

sinϕ=a/b

ϕ = 180  arcsin(x_o/x)

gdzie:

x₀ - odległość między osią OY i przecięciem się elipsy i osi OX,

x - odległość między osią OY, a punktem styczności elipsy i kursora pionowego.

Również w tym przypadku na błąd wpływa niedokładność odczytania wartości x i x₀ z ekranu oscyloskopu.

Podczas pomiarów błędy są spowodowane również niedokładnością wykonania elementów tworzących układ pomiarowy oraz niepewnymi połączeniami (styki).

Jednak naszym zdaniem decydujący wpływ na wyniki pomiarów ma ograniczona możliwość dokładnego odczytu wartości potrzebnych do obliczenia amplitudy, okresu oraz kąta przesunięcia fazowego.

Gen.

a

b

---