|
Wydział Elektroniki Politechniki Wrocławskiej
|
Laboratorium fizyki ogólnej
|
||
Wykonał Sławomir Wołek
|
Grupa
|
Ćw. nr 28 |
Prowadzący mgr.Sitarek |
|
Pomiar przewodności cieplnej izolatorów |
Data wykonania 99.03.09 |
Data oddania 99.03.16 |
Ocena
|
|
CEL ĆWICZENIA:
Zapoznanie z metodą pomiaru współczynnika przewodności cieplnej izolatorów oraz dokonanie tego pomiaru.
WSTĘP:
Jeżeli przeciwległe ścianki płyty o powierzchni S i grubości d1 mają odpowiednio temperatury T1 i T2 (T1>T2) , to następuje przepływ ciepła w kierunku powierzchni o niższej temperaturze .Ilość ciepła Q przepływającego w jednostce czasu w stanie stacjonarnym wyrazi się wzorem :
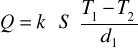
gdzie k to współczynnik przewodności cieplnej, oznacza ilość ciepła przechodzącego w jednostce czasu przez jednostkę powierzchni przy jednostkowym gradiencie temperatury .
Różne ciała mają różne wartości przewodności cieplnej .Ciała o małej wartości współczynnika przewodności cieplnej 10-1-10-2 J/(msK) nazywają się izolatorami .
Płytka bakelitowa, której współczynnik przewodności cieplnej k należy wyznaczyć jest okrągła więc można napisać :
![]()
r1-promień płytki.
Z powyższego wzoru wynika, że by wyznaczyć współczynnik przewodności cieplnej płytki, należy zmierzyć jej grubość d1, promień r1, temperatury T1 i T2 przeciwległych powierzchni oraz ilość ciepła Q przechodzącą w jednostce czasu między tymi powierzchniami .Ta ilość ciepła jest bezpośrednio trudna do zmierzenia, dlatego wyznacza się ją pośrednio metodą stygnięcia.
Jeżeli szybkość stygnięcia jest n, to ilość wypromieniowanego ciepła w jednostce czasu jest równa mcn, gdzie m oznacza masę mosiężnej płyty, a c to ciepło właściwe mosiądzu. Zakładając, że ilość wypromieniowanego ciepła jest proporcjonalna do powierzchni , można wyrazić ilość ciepła wypromieniowaną przez jednostkę powierzchni płyty w jednostce czasu jako:
![]()
gdzie r - promień płytki mosiężnej,
d - grubość płytki mosiężnej.
Uwzględniając, że po ustaleniu się temperatur ilość ciepła przewodzona przez płytkę bakelitową jest równa ilości ciepła wypromieniowanej przez boczną i dolną powierzchnię płyty mosiężnej można napisać :
![]()
czyli
![]()
Powyższy wzór wyprowadzono przy założeniu, że prąd ciepła jest normalny do powierzchni płytki bakelitowej. Warunek ten nie jest całkowicie spełniony ze względu na wypromieniowanie ciepła z brzegów płytki bakelitowej.
Ponadto szybkość stygnięcia płytki mosiężnej w stanie stacjonarnym może być nieco różna od wyznaczonej doświadczalnie, ze względu na większy wpływ prądów konwekcyjnych na stygnięcie powierzchni górnej płytki P2 niż dolnej .Ponadto założenie proporcjonalności ciepła wypromieniowanego do wielkości powierzchni jest pewnym przybliżeniem.
Błąd względny obliczamy ze wzoru :
![]()
a błąd bezwzględny ze wzoru :
![]()
WYKAZ PRZYRZĄDÓW :
• mosiężna puszka o grubym dnie P1
• mosiężna płytka P2 na trzech izolujących nóżkach
• płytka bakelitowa P
• ultratermostat Höpplera
• stoper
• multimetr elektroniczny
• suwmiarka
PRZEBIEG ĆWICZENIA :
1.Plan ćwiczenia.
Z ultratermostatu, połączonego wężami gumowymi , jest nagrzewana puszka P1, a następnie ciepło jest przewodzone przez płytkę P do płyty P2.
Układ płyt ogrzewa się do momentu ustalenia się temperatury T1 górnej płyty i temperatury T2 dolnej płyty .Można wtedy przyjąć , że temperatura górnej powierzchni płytki bakelitowej jest równa temperaturze puszki T1, a T2 jest równa temperaturze dolnej powierzchni płytki bakelitowej.Ustalenie się temperatur zachodzi, gdy ilość ciepła przewodzona przez płytkę bakelitową jest równa ilości ciepła wypromieniowanej przez dolną płytę .Aby określić tę ilość ciepła , należy wyznaczyć szybkość stygnięcia dolnej płytki w pobliżu temperatury T2 .W tym celu , po wyjęciu bakelitowej płytki , ogrzewa się dolną płytkę do temperatury T2+3K, a następnie po zdjęciu puszki wyznacza się szybkość jej stygnięcia .W jednostkowych odstępach czasu (co 10 s) mierzy się temperaturę do chwili gdy temperatura dolnej płyty będzie równa T2-4K .Szybkość stygnięcia mierzona jest dwukrotnie .
Przebieg chłodzenia należy przedstawić graficznie odkładając na osi rzędnych temperatury T, a na osi odciętych czas t .
2.Przebieg pomiarów.
Średnica płytki bakelitowej 2r1= 149,7 mm , promień r1= (74.85![]()
0,1) mm
Grubość płytki bakelitowej d1= (3,2![]()
0,1) mm
Średnica płytki mosiężnej P2 2r= 152 mm , promień r= (76![]()
0,1) mm
Grubość płytki mosiężnej P2 d= (12![]()
0,1) mm
Masa płytki mosiężnej P2 m= (1699![]()
0,2) g
Ciepło właściwe mosiądzu c= (375![]()
40) J/(![]()
)
Puszka P1 została podgrzana do temperatury T1=80˚C=353K
2a.Pierwszy pomiar.
Temperatura płytek ustaliła się na T1-T2=23,6˚C=296,6K
Tabela pomiarów |
t [ s ] |
T1-T2 [ ˚C ] |
Δ(T1-T2) [ ˚C ] |
n [˚C/s ] |
Δn |
0 |
20,6 |
|
|
|
10 |
20,9 |
0,3 |
0,03 |
0,0116 |
20 |
21,1 |
0,2 |
0,02 |
0,0016 |
30 |
21,3 |
0,2 |
0,02 |
0,0016 |
40 |
21,5 |
0,2 |
0,02 |
0,0016 |
50 |
21,7 |
0,2 |
0,02 |
0,0016 |
60 |
21,9 |
0,2 |
0,02 |
0,0016 |
70 |
22,1 |
0,2 |
0,02 |
0,0016 |
80 |
22,3 |
0,2 |
0,02 |
0,0016 |
90 |
22,6 |
0,3 |
0,03 |
0,0116 |
100 |
22,7 |
0,1 |
0,01 |
-0,0084 |
110 |
22,9 |
0,2 |
0,02 |
0,0016 |
120 |
23,1 |
0,2 |
0,02 |
0,0016 |
130 |
23,3 |
0,2 |
0,02 |
0,0016 |
140 |
23,5 |
0,2 |
0,02 |
0,0016 |
150 |
23,7 |
0,2 |
0,02 |
0,0016 |
160 |
23,9 |
0,2 |
0,02 |
0,0016 |
170 |
24,1 |
0,2 |
0,02 |
0,0016 |
180 |
24,3 |
0,2 |
0,02 |
0,0016 |
190 |
24,5 |
0,2 |
0,02 |
0,0016 |
200 |
24,6 |
0,1 |
0,01 |
-0,0084 |
210 |
24,8 |
0,2 |
0,02 |
0,0016 |
220 |
25,0 |
0,2 |
0,02 |
0,0016 |
230 |
25,2 |
0,2 |
0,02 |
0,0016 |
240 |
25,3 |
0,1 |
0,01 |
-0,0084 |
250 |
25,5 |
0,2 |
0,02 |
0,0016 |
260 |
25,7 |
0,2 |
0,02 |
0,0016 |
270 |
25,8 |
0,1 |
0,01 |
-0,0084 |
280 |
26,0 |
0,2 |
0,02 |
0,0016 |
290 |
26,1 |
0,1 |
0,01 |
-0,0084 |
300 |
26,3 |
0,2 |
0,02 |
0,0016 |
310 |
26,5 |
0,2 |
0,02 |
0,0016 |
320 |
26,7 |
0,2 |
0,02 |
0,0016 |
330 |
26,8 |
0,1 |
0,01 |
-0,0084 |
340 |
27,0 |
0,2 |
0,02 |
0,0016 |
350 |
27,1 |
0,1 |
0,01 |
-0,0084 |
360 |
27,3 |
0,2 |
0,02 |
0,0016 |
370 |
27,5 |
0,2 |
0,02 |
0,0016 |
375 |
27,6 |
0,1 |
0,02 |
0,0016 |
n=(0,0184![]()
0,0033)˚C/s
Krzywa stygnięcia
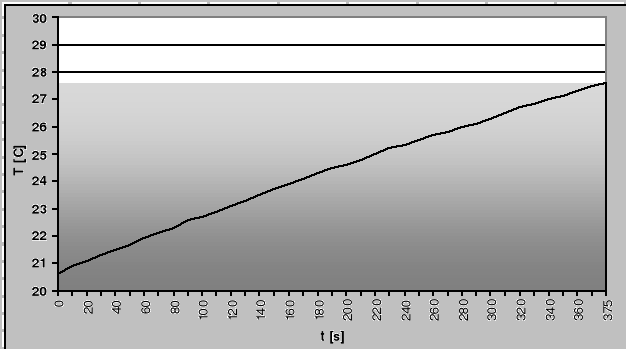
Współczynnik przewodności cieplnej badanej płytki bakelitowej wynosi :
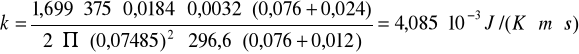
Pomiar błędów :

2b.Drugi pomiar.
Temperatura równowagi ustaliła się na poziomie T1-T2=13,4 ˚C=286,4K
Tabela drugiego pomiaru |
t [ s ] |
T1-T2 [ ˚C] |
Δ(T1-T2)[˚C] |
n [ ˚C/s ] |
Δn |
0 |
10,4 |
|
|
|
10 |
10,8 |
0,4 |
0,04 |
0,007 |
20 |
11,2 |
0,4 |
0,04 |
0,007 |
30 |
11,7 |
0,5 |
0,05 |
0,017 |
40 |
12,1 |
0,4 |
0,04 |
0,007 |
50 |
12,6 |
0,5 |
0,05 |
0,017 |
60 |
13,0 |
0,4 |
0,04 |
0,007 |
70 |
13,4 |
0,4 |
0,04 |
0,007 |
80 |
13,7 |
0,3 |
0,03 |
-0,003 |
90 |
14,1 |
0,4 |
0,04 |
0,007 |
100 |
14,4 |
0,3 |
0,03 |
-0,003 |
110 |
14,7 |
0,3 |
0,03 |
-0,003 |
120 |
15,0 |
0,3 |
0,03 |
-0,003 |
130 |
15,3 |
0,3 |
0,03 |
-0,003 |
140 |
15,6 |
0,3 |
0,03 |
-0,003 |
150 |
15,9 |
0,3 |
0,03 |
-0,003 |
160 |
16,2 |
0,3 |
0,03 |
-0,003 |
170 |
16,4 |
0,2 |
0,02 |
-0,013 |
180 |
16,7 |
0,3 |
0,03 |
-0,003 |
190 |
17,0 |
0,3 |
0,03 |
-0,003 |
200 |
17,2 |
0,2 |
0,02 |
-0,013 |
210 |
17,4 |
0,2 |
0,02 |
-0,013 |
n=(0,033![]()
0,007)[ ˚C/s ]
Krzywa stygnięcia
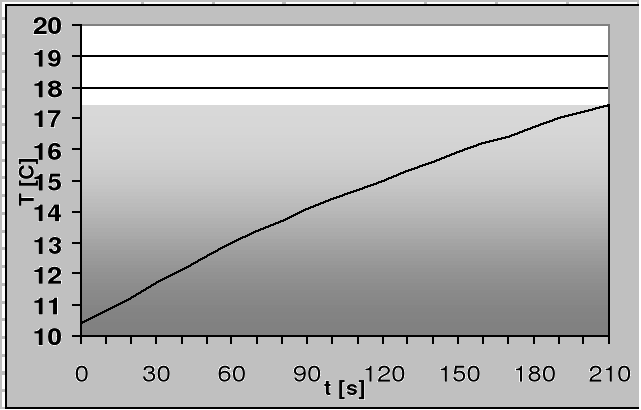
Współczynnik przewodności badanej płytki bakelitowej wynosi :
![]()
Pomiar błędów

WNIOSKI I UWAGI:
Dokonaliśmy dwóch pomiarów współczynnika przewodności cieplnej tego samego izolatora .Jako izolator służyła płytka bakelitowa .
Bardzo duży błąd bezwzględny wnoszą :
• stała ciepła właściwego
• fakt , że płytka izolatora wypromieniowuje ciepło również z brzegów
• szybsze stygnięcie górnej powierzchni płytki mosiężnej spowodowane konwekcją
Bardzo duża rozbieżność w otrzymanych wartościach w dwóch pomiarach
wynika z niemożności zapewnienia w ćwiczeniu warunków laboratoryjnych
(m.in. stałej temperatury zewnętrznej układu) oraz błędów przyrządów .
Nie mniej jednak otrzymane wartości współczynnika przewodności cieplnej
mieszczą się w obliczonych granicach błędów ( w pierwszym pomiarze
k=[ 2,471 ; 5,699 ] , w drugim natomiast k=[ 4,223 ; 10,937 ] ).
W przypadku pomiaru średnicy płyty błąd względny miał mniejszą
wartość od dokładności suwmiarki .Przyjęto więc jako błąd dokładność suwmiarki .
Wyszukiwarka