1 PRACOWNIA FIZYCZNA		Nazwisko i imię:
Uniwersytet Pedagogiczny-KRAKÓW		KIER.:	ROK:	GRUPA:
NR Ćw.: 4	TEMAT ĆW.: WYZNACZANIE WSPÓŁCZYNNIK ZAŁAMANIA ŚWIATŁA METODĄ SZPILEK
DATA WYK.:	UWAGI:				ZALICZENIE
I część teoretyczna II Wyniki pomiarów III Opracowanie pomiarów i wnioski

Prawo odbicia i załamania światła

Prawo odbicia światła

Kąt odbicia światła jest równy kątowi padania, przy czym promień padający, odbity i prosta prostopadła do powierzchni granicznej poprowadzona w punkcie padania leżą w jednej płaszczyźnie.

 

 

Prawo załamania światła

Zmiana kierunku promieni świetlnych podczas załamania nie jest przypadkowa. Opisuje to prawo załamania światła nazywane niekiedy prawem Snelliusa.

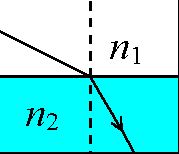
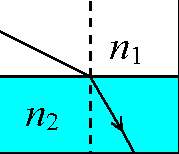
Prawo załamania światła łączy ze sobą dwa kąty - kąt padania na powierzchnię rozgraniczającą dwa ośrodki i kąt załamania powstający gdy promień przejdzie granicę i zacznie się rozchodzić w drugim ośrodku (patrz rysunek niżej).

Warto zwrócić uwagę na fakt, że kąty padania i załamania są liczone od normalnej do powierzchni, a nie od samej powierzchni.

Prawo załamania - postać 1 - podstawowa

		α - kąt padania β - kąt załamania v1 - prędkość światła w ośrodku 1 v2 - prędkość światła w ośrodku 2
Słownie prawo załamania można sformułować następująco: Stosunek sinusa kąta padania, do sinusa kąta załamania jest dla danych ośrodków stały i równy stosunkowi prędkości fali w ośrodku pierwszym, do prędkości fali w ośrodku drugim. Kąty padania i załamania leżą w tej samej płaszczyźnie.Inne postacie prawa załamania Zdefiniujmy wielkość zwaną bezwzględnym współczynnikiem załamania ośrodka:
	v - prędkość światła w ośrodku c - prędkość światła w próżni (c = 299 792 458 m/s) n - bezwzględny współczynnik załamania
Podstawmy teraz tę wielkość do wzoru na prawo załamania, zmieniając nieco postać - tzn. wyliczając prędkość v (wzór otrzymujemy mnożąc obie strony ostatniego równania przez v i dzieląc przez n):
Podstawimy ten wzór raz w wersji dla ośrodka 1  (n1 - bezwzględny współczynnik załamania w ośrodku 1)   A potem w wersji dla ośrodka 2  (n2 - bezwzględny współczynnik załamania w ośrodku 2)

Wtedy otrzymamy:
		n1 - bezwzględny współczynnik załamania ośrodka 1 n2 - bezwzględny współczynnik załamania ośrodka 2 c - prędkość światła w próżni
Stąd ostatecznie będziemy mieli drugą postać prawa załamania światła. Wzór prawa załamania - postać 2   Ta wersja prawa załamania wiąże kąty padania i załamania z bezwzględnymi współczynnikami załamania w obu ośrodkach. Sformułowanie słowne: Stosunek sinusa kąta padania, do sinusa kąta załamania jest równy stosunkowi bezwzględnego współczynnika załamania ośrodka do którego przechodzi fala, do bezwzględnego współczynnika załamania ośrodka, z którego fala pada na powierzchnię rozgraniczającą oba ośrodki. Wzór prawa załamania - postać 3 Jest jeszcze trzecia postać prawa załamania. Powstaje ona po zdefiniowaniu kolejnej wielkości zwanej względnym współczynnikiem załamania:
		n1 - bezwzględny współczynnik załamania ośrodka 1 n2 - bezwzględny współczynnik załamania ośrodka 2 n12 - współczynnik załamania (względny) ośrodka 2 względem ośrodka 1
Warto zwrócić uwagę na fakt, że względny współczynnik załamania czyta się od tyłu: - jest to współczynnik załamania ośrodka drugiego (do którego wchodzi światło) względem ośrodka pierwszego (z którego przychodzi światło). Po podstawieniu względnego współczynnika załamania do 2 postaci prawa załamania otrzymamy: Zatem:   stosunek sinusa kąta padania do sinusa kąta załamania jest równy względnemu współczynnikowi załamania światła ośrodka do którego światło wpada względem ośrodka z którego światło wychodzi.

Względny i bezwzględny współczynnik załamania światła

Bezwzględny współczynnik załamania światła

Bezwzględny współczynnik załamania światła dany jest wzorem 

v - prędkość światła w danym ośrodku
c - prędkość światła w próżni (c = 299 792 458 m/s)
n - bezwzględny współczynnik załamania

Znajomość bezwzględnych współczynników załamania umożliwia szybkie obliczenie prędkości światła w danych ośrodku, wg wzoru:

 

Przykład:

Prędkość światła w szkle wynosi ok. 2/3 prędkości światła w próżni. Współczynnik załamania szkła wynosi więc 3/2 - 1,5.

Względny współczynnik załamania światła

Mając bezwzględne współczynniki załamania ośrodka z którego pada światło i ośrodka do którego załamuje się światło, można obliczyć względny współczynnik załamania :

 

n₁ - bezwzględny współczynnik załamania ośrodka 1 (z którego wychodzi światło)

n₂ - bezwzględny współczynnik załamania ośrodka 2 
(do którego przechodzi światło)

n₁₂ - współczynnik załamania (względny) ośrodka 2 względem ośrodka 1

Względny współczynnik załamania decyduje o tym jak bardzo światło ma tendencję do skręcania swego kierunku podczas przechodzenia do innego ośrodka. Inaczej mówiąc -  przy dużym względnym współczynniku załamania światło będzie się silniej załamywać.

W przypadku, gdy nie ma dokładnego stwierdzenia o jaki współczynnik chodzi, najczęściej samo wyrażenie "współczynnik załamania" należy rozumieć jako "bezwzględny współczynnik załamania".

Przykładowe (bezwzględne) współczynniki załamania

diament: 2,47
lód: 1,31
szkło: ok. 1,5 (wielkość zależna od rodzaju szkła, waha się od ok. 1,45 do 1,8)
woda: 1,33

Przejście światła białego przez płytkę płasko-równoległą.

jeżeli promienie świetlne padają na płytkę płasko-równoległą (przy czym pierwszy i ostatni jest identyczny) to promień wychodzący ma kierunek równoległy od padającego i jest przesunięty względem niego.

Rysunek 1. Załamanie światła w płytce płasko-równoległej : α- kat padania, β - kat załamania

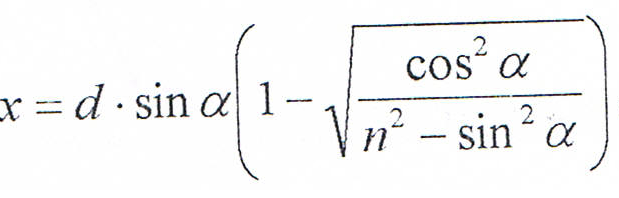
przesuniecie x promienia dla zwykłej płytki:

d-grubość nitki, jest współczynnikiem załamania światła.

Przejście światła białego przez pryzmat.

Pryzmatem nazywamy część ciała przezroczystego(o współczynniku załamania n) ograniczoną dwiema płaszczyznami o wspólnej krawędzi. Kąt wierzchołkowy φ między tymi półpłaszczyznami nazywamy kątem łamiącym pryzmatu.

Kąt odchylenia jest tym większy, im większy jest kąt łamiący i im większy jest współczynnik załamania szkła, z którego jest wykonany pryzmat. Jeżeli przez otworek w zasłonie okiennej puścić na pryzmat promień światła słonecznego, to na ekranie ustawionym za pryzmatem widoczna będzie barwna smuga. Promień światła białego ulegnie rozszczepieniu na promienie barwne. Światło białe jest więc mieszaniną barw, które w szkle biegną z różnymi prędkościami i każda z nich wywołuje w oku wrażenie innej barwy. Barwna smuga na ekranie nazywa się widmem.

            Oko jest czułe na widmo tego zasięgu barw od czerwonej, przez pomarańczową, żółtą, zieloną, niebieską do fiołkowej. Najsłabiej załamuje się w pryzmacie światło czerwone, najsilniej - fioletowe. W widmie można jeszcze stwierdzić obecność światła, na które oko nie jest wrażliwe. Jeśli poza czerwoną częścią widma umieścić zaczernioną banieczkę termometru, to można zauważyć, że poziom rtęci w rurce termometru podnosi się. Ta niewidzialna część widma, wywołująca zjawiska cieplne, nosi nazwę podczerwieni. 

Opracowanie i wnioski:

Podczas tego doświadczenia uzyskałem dość dokładne wyniki zarówno dla płytki jak i dla pryzmatu. Współczynnik załamania światła dla płytki(plexiglas) wyniósł n=1.24,a dokładność pomiaru wynosiła 0,05% zaś dla pryzmatu(szkło) n=1,55 i dokładności 0,01%. Te niewielkie odchylenia od wartości tablicowych były spowodowane czynnikiem ludzkim np. drżąca ręka(szpilka przesunięta w jedna lub druga stronę) , ewentualne wady wzroku, grubość prowadzonych linii co miało wpływ na odczytanie uzyskanych wartości.

Sprawozdanie z ćw.4

1 | Strona

---