Materiały pomocnicze do egzaminu z PODSTAW MATEMATYKI

(I część)

1. Podaj określenie ciągu liczbowego (podaj przykład).

2. Podaj dwa pierwsze wyrazy ciągu o wyrazie ogólnym:
   .

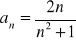
3. Jak nazywamy ciągi w których:

1. 
   ,

2. 
   ?

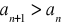
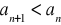
4. Zapisz ciąg ograniczony a_n, którego wyrazy lezą w przedziale (m;M).

5. Czym charakteryzuje się ciąg będący postępem arytmetycznym? (Wykorzystaj odpowiednie zapisy.)

6. Które ciągi nazywamy ciągami monotonicznymi?

7. Zbadaj, czy ciąg
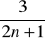
   jest ciągiem monotonicznym.

8. Jak określamy ciąg będący postępem geometrycznym?

9. Jaka istotna różnica zachodzi między postępem arytmetycznym a geometrycznym?

10. Napisz trzy początkowe wyrazy postępu geometrycznego, w którym:

1. 
   ,
   ,

2. 
   ,
   ,

3. 
   ,
   .

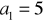
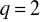
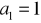
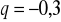
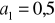
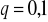
11. Podaj określenie pojęcia funkcji
    .

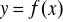
12. Czy ciężar (waga) człowieka jest funkcją wzrostu? Uzasadnić.

13. Określona jest funkcja
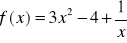
    . Znaleźć wartość podanej funkcji dla:

x=2; x=a; x=0.

14. Podaj warunki jakie musi spełniać funkcja monotoniczna; zapisz formalnie chociaż jeden z warunków monotoniczności funkcji.

15. Podaj (zapisz) warunek funkcji różnowartościowej.

16. Znajdź miejsca zerowe funkcji
    .

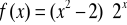
17. Jak określamy funkcję złożoną typu
    ,
    ?

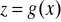
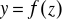
18. Z jakich funkcji złożona jest funkcja:

1. 
   ,

2. 
   ,

3. 
   .

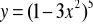
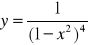
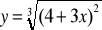
19. Granica funkcji w punkcie x₀. Określenie granicy przy
    lub
    .

20. Obliczyć:

a)
, d)
,

b)
, e)
,

c)
, f)
.

21. Funkcje ciągłe. Należy pamiętać, że granica funkcji w punkcie (np. a) i wartość funkcji w punkcie są to różne pojęcia. W pierwszym przypadku postrzegamy co się dzieje, gdy wartości x zbliżają się do a, nie mamy natomiast informacji co zachodzi w samym punkcie a. Funkcja może mieć granicę, a nie mieć wartości w punkcie a, ale może być i tak, że w jakimś punkcie funkcja ma wartość a nie ma granicy.

22. Podaj określenie funkcji ciągłej w punkcje x=a.

Co można powiedzieć o sumie, różnicy i iloczynie funkcji ciągłych w danym punkcie?

Czy funkcja złożona z funkcji ciągłych jest ciągła w każdym punkcie, w którym jest określona (uzasadnij).

23. Podaj określenie funkcji ciągłej w przedziale
.

24. Pochodna funkcji. Zapisz pochodną funkcji w punkcie x₀ za pomocą ilorazu różnicowego funkcji f.

25. Istnienie pochodnej funkcji f w każdym punkcie pewnego zbioru X oznacza istnienie nowej funkcji zwanej…..

26. Wykorzystując definicję pochodnej, wykaż, że funkcja
ma w każdym punkcie
pochodną równą
.

27. Znaleźć pochodne funkcji korzystając z jej definicji:

a)
,

b)
,

c)
,

d)
.

28. Reguły różniczkowania funkcji elementarnych (bez funkcji trygonometrycznych)

29. Obliczyć pochodne funkcji:

a)
, f)
,

b)
, g)
,

c)
, a - stała, h)
,

d)
, i)
, a, b - stałe.

e)
,

30. Ekstrema funkcji. Podać definicje maksimum i minimum lokalnego funkcji
.

31. Warunek konieczny istnienia ekstremum funkcji różniczkowalnej.

32. Warunek dostateczny istnienia ekstremum funkcji różniczkowalnej.

33. Znaleźć ekstrema funkcji:

a)
, b)
, c)
.

34. Zastosowania pochodnej - koszt całkowity, koszt krańcowy, utarg krańcowy. Elastyczność funkcji.

2

---