Rozwiązania zadań - temat 12
8*/131
I = 1B, pKw = 13,73 w T = 298 K (Tabela I, str. 249 w skrypcie)
pKw = pcH + pcOH; [H+] = 10-pcH ·co
pcOH = 2,93, pcH = 13,73 - 2,93 = 10,80; [H+] = 1.6·10-11 mol/dm3
pcOH = 5,18, pcH = 13,73 - 5,18 = 8,55; [H+] = 2,8·10-9 mol/dm3
pcOH = 8,63, pcH = 13,73 - 8,63 = 5,10; [H+] = 7,9·10-6 mol/dm3
pcOH = 12,85, pcH = 13,73 - 12,85 = 0,88; [H+] = 1,3·10-1 mol/dm3
15/131
I = 3A, pKw = 14,20 w T = 298 K (Tabela I, str. 249 w skrypcie)
R1)
V1 = 200 cm3 mocnego kwasu HX, [H+] = 0,20 mol/dm3
HX →H+ + X- , stąd cHX = 0,20 mol/dm3
R2)
V2 = 150 cm3 mocnej zasady MOH, pcH = 11,50
MOH →M+ + OH-
pcOH = pKw - pcH = 14,20 - 11,50 = 2,70,
stąd cMOH = [OH-] = 10-pcOH ∙co = 2,00∙10-3 mol/dm3 ( trzy cyfry znaczące)
R3) Po zmieszaniu R1 i R2
MOH + HX = MX + H2O
noHX = V1∙cHX = 0,200∙0,20 = 0,0400 mol
noMOH = V2∙cMOH = 0,150 0,00200 = 3,00∙10-4 mol
Ponieważ noHX > noMOH, to n*MOH = noMOH, to ze stechiometrii równania reakcji zobojętniania wynika, że n*HX = noMOH. Stąd w uzyskanym roztworze pozostaje nadmiar niezobojętnionego kwasu HX: nHX = noHX - n*HX = 0,0400 - 3,00∙10-4 = 0,0397 mol
Zakładamy addytywność objętości mieszanych roztworów:
V3 = V1 + V2 = 0,200 + 0,150 = 0,350 dm3
c'HX = nHX/V3 = 0,0397/0,350 = 0,113 mol/dm3
[H+]R3 = c'HX = 0,11 mol/dm3 (dwie cyfry znaczące)
19*/132
CH3COOH ↔ H+ + CH3COO-
Ogólnie: HA ↔ H+ + A-
I = 1A, pKa = 4,55 w T = 298 K (Tabela II, str.250-251 w skrypcie)
Ka = 10-4,55 = 2,82·10-5 (trzy cyfry znaczące!)
cHA = 1,7 mol/dm3
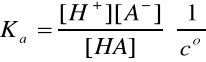
Ponieważ: [H+] = [A-]
oraz
[HA] = cHA - [H+]
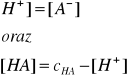
to
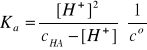
Założenie:
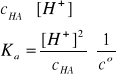
![]()
![]()
Założenie jest bardzo dobrze spełnione, ponieważ cHA 177 razy większe od [H+].
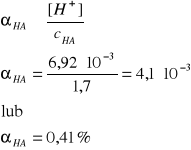
21*/132
NH4OH↔NH4+ + OH-
Ogólnie: BOH↔B+ + OH-
I = 2A, pKb = 4,40 w T = 298 K (Tabela V, str. 256-257 w skrypcie)
pKw = 13,97 w T = 298 K (Tabela I, str. 249 w skrypcie)
Kb = 10-4,40 = 3,98·10-5 (trzy cyfry znaczące!)
p[%]NH3 = 2,7%, d = 1,15 g/cm3, Vr ≡ 1 dm3
mr = Vr·d = 1000·1,15 = 1150 g
mNH3 = mr· p[%]NH3/100 = 1150·2,7/100 = 31.0 g NH3
MNH3 = 17,031 g/mol
nNH3 = 31,0/17,031 = 1,82 mol
cNH3 = 1,82 mol/dm3
Przyjmujemy, że: cNH4OH = cNH3
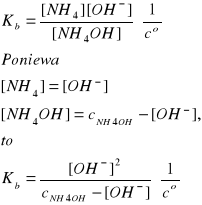
Założenie:
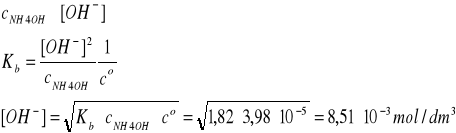
Założenie jest bardzo dobrze spełnione, ponieważ cNH4OH jest 214 razy większe od [OH-].
![]()
pcH + pcOH = pKw, pcH = pKw - pcOH = 13,97 - 2,07 = 11,90
23*/132
A - kwas solny
HCl→H+ + Cl-, pcH1 = 4,26,
pcH = -log[H+]/co = -logcHCl/co; cHCl = 10-pcH ·co = 5,50·10-5 mol/dm3
R = 25, c'HCl = cHCl/R = 2,20·10-6 mol/dm3
pcH2 = - log c'HCl/co = 5,65
B - kwas cyjanowodorowy
HCN↔H+ + CN-, pcH1 = 4,26
I = 2A, pKa = 8,52 (Tabela 2); Ka = 3,02·10-9
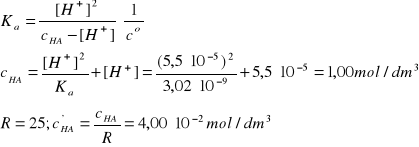
Założenie: c'HA>>[H+]'
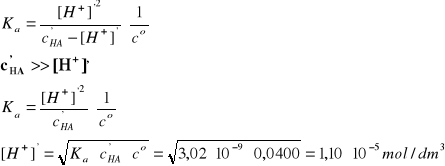
Założenie jest znakomicie spełnione, c'HA jest 3636 razy większe od [H+]'.
pcH2 = -log [H+]'/co = 4,96
22/131
HCOOH↔H+ + HCOO-, ogólnie HA ↔ H+ + A-
I = 3A, pKa = 3,90 w T = 298 K (Tabela II, str.250-251 w skrypcie),
Ka = 1,26·10-4 (trzy cyfry znaczące)
p[%]HA = ?, Vr ≡ 1dm3, dr = 1,22 g/cm3, pcH = 1,79
[H+] = 10-pcH ∙co = 0,0162 mol/dm3 (trzy cyfry znaczące)
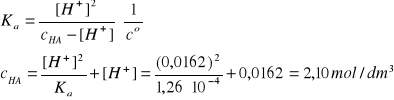
nHA = Vr∙cHA = 2,10 mol, MHCOOH = 46,03 g/mol
mHA = 2,10∙46,03 = 96,7 g
p[%]HA = 100∙mHA/mr = 100∙mHA/Vr∙dr = 100∙96,7/1220 = 7,9% (dwie cyfry znaczące)
25/132
Kwas propionowy, HA, a) 0,010 mol/dm3 , b) 0,050 mol/dm3
I = 1A, pKa = 4,66 w T = 298 K (Tabela II, str.250-251 w skrypcie), Ka = 2,19∙10-5 (trzy cyfry znaczące)
HA ↔ H+ + A
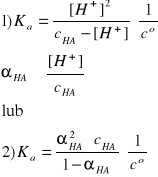
Ponieważ obydwa stężenia kwasu są małe, to należy się spodziewać, że jego stopnie dysocjacji będą większe od 0,01, tzn. większe od 1%. Zatem, należy rozwiązać równania kwadratowe zupełne względem stężenia jonów H+ lub stopnia dysocjacji αHA.
Dla ilustracji postępowania w obydwu przypadkach rozwiążemy kolejno równanie (1) dla cHA = 0,010 mol/dm3 i równanie (2) dla cHA = 0,050 mol/dm3.
a) 0,01 M HA
[H+]2 + Ka[H+] - KacHA = 0
[H+]2 + 2,19∙10-5[H+] - 2,19∙10-7 = 0
Δ = (2,19·10-5)2 + 4∙2,19∙10-7 = 8,76480∙10-7 (sześć cyfr znaczących, bo do dalszych obliczeń bierzemy pierwiastek kwadratowy wyróżnika!)
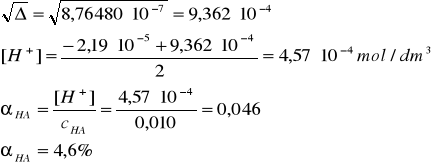
b) 0,050 M HA
cHA·(αHA)2 + KaαHA - Ka = 0
0,050·(αHA)2 + 2,19·10-5·αHA - 2,19·10-5 = 0
Δ = (2,19·10-5)2 + 4·0,050·2,19·10-5 = 4,38048·10-6 (sześć cyfr znaczących!)
![]()
= 2,093·10-3
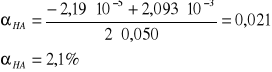
UWAGA: Wzór (2) to tkz. prawo rozcieńczeń Ostwalda, z którego wynika, że stopień dysocjacji słabego elektrolitu (tutaj kwas propionowy) wzrasta wraz z rozcieńczeniem roztworu. Innymi słowy, gdy stężenie słabego elektrolitu maleje, to jego stopień dysocjacji wzrasta.
28*/132
HClO2 ↔ H+ + ClO2-
I = 1A, pKa = 1,61 w T = 298 K (Tabela II, str.250-251 w skrypcie), Ka =2,45·10-2
α = 46,0% czyli 0,460
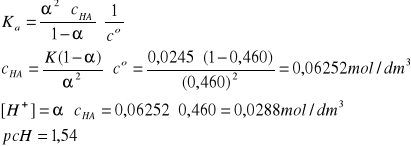
29*/132
HN3 ↔H+ + N3-
I = 3A, pKa = 4,78 w T = 298 K (Tabela II, str.250-251 w skrypcie), Ka = 1,66·10-5
R1: V1 = 100 cm3, c1 = 0,10 M HN3
R2: V2 = 100 cm3 HN3 o pcH = 2,69
[H+]2 = 2,04·10-3 mol/dm3 (trzy cyfry znaczące)
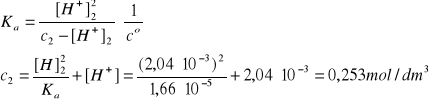
R3: Zakładamy addytywność objętości
V3 = V1 + V2 = 0,100 + 0,100 = 0,200 dm3
Obliczamy liczność kwasu azotowodorowego w uzyskanym roztworze:
nHN3 = V1c1 + V2c2 = 0,100·0,10 + 0,100·0,253 = 0,0353 mol/dm3
c3 = nHN3/V3 = 0,0351/0,200 = 0,176 mol/dm3
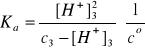
Założenie: c3 >> [H+]3
[H+]3 = (Kac3)1/2 = 1,71·10-3
Powyższe założenie jest spełnione, c3 jest 103 razy większe od [H+]3. Zatem:
α = [H+]3/c3 = 0,0097 lub 0,97%.
11/a.c.d - I = 3A, pKw = 14,20 (Tabela 1, str. 249)
p[%] = 1,00% NaOH, d = 1,22 g/cm3 V ≡1 dm3 = 1000 cm3, MNaOH = 40,01 g/mol
mr = V∙d = 1000∙1,22 = 1220 g
mNaOH = mr∙p[%]/100 = 12,20 g
nNaOH = mNaOH/MNaOH = 12,20/40,01 = 0, 3049 mol
cNaOH = 0,3049 mol/dm3
NaOH → Na+ + OH-
[OH-] = 0,3049 mol/dm3
pcOH = 0,516
pcH = pKw - pcOH = 14,20 - 0,516 = 13,68
cHNO3 = 0,34 mol/m3 = 3,4∙10-4 mol/dm3
HNO3 → H+ + NO3-
[H+] = cHNO3
pcH = 3,47
pcOH = pKw - pcH = 14,20 - 3,47 = 10,73
cKOH = 0,53 mol/dm3
KOH → K+ + OH-
[OH-] = cKOH
pcOH = 0,26
pcH = pKw - pcOH = 14,20 - 0,26 = 13,94
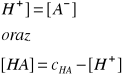
Wyszukiwarka