2010/2011

Odpowiedzi do zadań z matematyki dla Towaroznawstwa

Zestaw IV c.d.

Zadanie 5

1. 
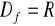
   , miejsce zerowe: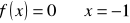
   ,

,

maksimum lokalne dla
, wartość maksymalna
,

funkcja rosnąca dla
i malejąca dla
,

funkcja wklęsła dla
i wypukła dla
,

punkt przegięcia w
.

2. 
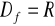
   , miejsce zerowe: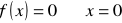
   ,

,

maksimum lokalne dla
, wartość maksymalna
,

minimum lokalne dla
, wartość minimalna
,

funkcja malejąca dla
i rosnąca dla
,

funkcja wklęsła dla
i wypukła dla
,

dwa punkty przegięcia:
oraz
.

3. 
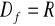
   , nie ma miejsc zerowych,

,

nie ma ekstremów

funkcja rosnąca dla
, czyli w całej dziedzinie poza punktem
,

funkcja wklęsła dla
i wypukła dla
,

dwa punkty przegięcia
oraz
.

4. 
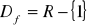
   , nie ma miejsc zerowych,

,
,
,

,
,

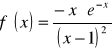
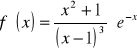
maksimum lokalne dla
, wartość maksymalna
,

funkcja rosnąca dla
i malejąca dla
,

funkcja wklęsła dla
i wypukła dla
,

brak punktów przegięcia.

5. 
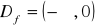
   , miejsce zerowe: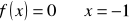
   ,

,

maksimum lokalne dla
, wartość maksymalna
,

funkcja rosnąca dla
i malejąca dla
,

funkcja wklęsła w całej dziedzinie,

nie ma punktów przegięcia.

6. 
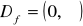
   , miejsce zerowe: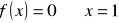
   ,

,

minimum lokalne dla
, wartość minimalna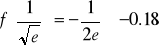
,

funkcja malejąca dla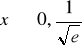
i rosnąca dla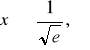
,

funkcja wklęsła dla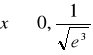
i wypukła dla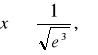
,

punkt przegięcia w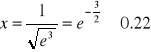
.

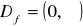
7. 
   , miejsce zerowe: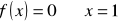
   ,

,

maksimum lokalne dla
, wartość maksymalna
,

funkcja rosnąca dla
i malejąca dla
,

funkcja wklęsła dla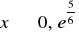
i wypukła dla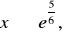
,

punkt przegięcia w
.

Zadanie 6

1. 
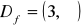
   , miejsce zerowe: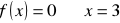
   ,

,

nie ma ekstremów ani punktów przegięcia,

funkcja rosnąca i wklęsła dla
,

2. 
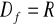
   , nie ma miejsc zerowych,

,
,

,
,

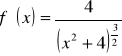
minimum lokalne dla
, wartość minimalna
,

funkcja malejąca dla
i rosnąca dla
,

funkcja wypukła w całej dziedzinie,

nie ma punktów przegięcia.

3. 
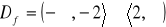
   , miejsca zerowe: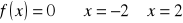
   ,

,
,
,
,

,
,

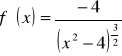
nie ma ekstremów ani punktów przegięcia,

funkcja malejąca dla
i rosnąca dla
,

funkcja wklęsła w całej dziedzinie.

4. 
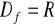
   , nie ma miejsc zerowych,

,
,

minimum lokalne dla
, wartość minimalna
,

funkcja malejąca dla
i rosnąca dla
,

funkcja wypukła w całej dziedzinie,

nie ma punktów przegięcia.

5. 
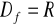
   , nie ma miejsc zerowych,

,
,

maksimum lokalne dla
, wartość maksymalna
,

funkcja rosnąca dla
i malejąca dla
,

funkcja wklęsła dla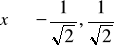
i wypukła dla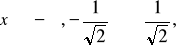
,

dwa punkty przegięcia:
oraz
.

6. 
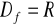
   , miejsce zerowe: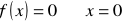
   ,

,
,

,
,

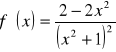
minimum lokalne dla
, wartość minimalna
,

funkcja malejąca dla
i rosnąca dla
,

funkcja wklęsła dla
i wypukła dla
,

dwa punkty przegięcia:
oraz
.

7. 
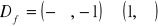
   , miejsca zerowe: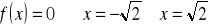
   ,

,
,
,
,

,
,

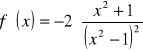
brak ekstremów i punktów przegięcia,

funkcja malejąca dla
i rosnąca dla
,

funkcja wklęsła w całej dziedzinie.

8. 
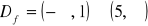
   , miejsca zerowe: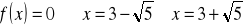
   ,

,
,
,
,

brak ekstremów i punktów przegięcia,

funkcja malejąca dla
i rosnąca dla
,

funkcja wklęsła w całej dziedzinie.

Zadanie 7

Obwód będzie najmniejszy, gdy prostokąt będzie kwadratem o bokach równych
.

Zadanie 8

Pole będzie największe, gdy prostokąt będzie kwadratem o bokach
.

Zadanie 9

Krawędzie podstawy powinny mieć długość 3 cm oraz 6 cm, a wysokość powinna być równa 4 cm.

Zadanie 10

Objętość prostopadłościanu będzie największa dla
. Długości krawędzi będą wtedy równe:
,
oraz
. Maksymalna objętość wynosi
.

Zadanie 11

Przekątna będzie najmniejsza, gdy prostopadłościan będzie sześcianem o krawędziach podstawy i wysokości równych
. Minimalna długość przekątnej wynosi
.

Zadanie 12

Koszt przebycia drogi będzie najmniejszy przy prędkości
.