|
Katedra Metrologii Politechniki Wrocławskiej |
Laboratorium Miernictwa Elektrycznego i Elektronicznego |
Wykonawca: Marcin Klekotko Wydział Elektroniki; kierunek AiR |
Ćwiczenie nr 1 (sala 4) Temat: Statystyczna analiza wyników pomiarowych |
|
Data wykonania ćwiczenia: 2000-03-13 |
Ocena: |
|
I. CEL ĆWICZENIA
Celem ćwiczenia jest zapoznanie studenta ze statystyczną analizą wyników pomiarów, w szczególności: sposobami znajdowania i eliminacji wyników pomiarów obarczonych ”błędami grubymi”, wyznaczania i analizy składowych przypadkowej i systematycznej błędów pomiarów.
II. OPIS ĆWICZENIA
Ćwiczenie realizowane jest na przykładzie pomiarów wymiarów liniowych trójkąta, boków a, b, c oraz odpowiednich wysokości ha, hb, hc. W trakcie ćwiczenia każdy student otrzymuje swój własny trójkąt oznaczony numerem n (n=1,2,...,N) oraz suwmiarkę o rozdzielczości 0.01 mm. Studenci mierzą swoje trójkąty, a następnie wymieniają je między sobą i mierzą trójkąty swoich kolegów. W rezultacie każdy student wypełnia tabelę, wzór poniżej, z pomiarami wszystkich trójkątów, które następnie wprowadza do komputera. Odpowiedni program komputerowy sporządza zbiorczy plik z pomiarami wszystkich studentów a inny program umożliwia każdemu studentowi wyselekcjonowanie wyników pomiarów jego trójkąta dokonanych przez wszystkich studentów w grupie. Program ten oblicza również pola trójkątów, wartości średnie i odchylenia standardowe boków, wysokości oraz pól.
III CZĘŚĆ POMIAROWA:
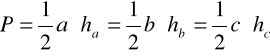
Pomiar pola trójkąta ze wzoru ogólnego:
Gdzie przykładowo: a - podstawa trójkąta
ha - wysokość trójkąta opuszczona na podstawę a
numer |
boki trójkąta |
|
|
wysokości trójkąta |
|
|
studenta |
a |
b |
c |
ha |
hb |
hc |
1 |
94,16 |
84,34 |
75,86 |
64,76 |
72,25 |
80,17 |
2 |
94,31 |
84,37 |
75,88 |
64,71 |
72,25 |
----------------- |
3 |
----------------- |
84,30 |
75,85 |
64,63 |
72,21 |
80,25 |
4 |
----------------- |
84,30 |
75,85 |
64,63 |
72,21 |
80,25 |
5 |
94,17 |
84,32 |
75,84 |
64,72 |
----------------- |
----------------- |
6 |
94,29 |
84,41 |
76,03 |
64,88 |
----------------- |
80,34 |
7 |
94,20 |
84,38 |
75,90 |
64,72 |
72,25 |
80,33 |
8 |
94,16 |
84,34 |
75,84 |
64,68 |
72,21 |
80,25 |
9 |
94,22 |
84,38 |
75,89 |
64,74 |
72,26 |
80,35 |
10 |
94,20 |
84,36 |
75,89 |
64,70 |
72,21 |
80,31 |
11 |
94,20 |
84,40 |
75,90 |
64,70 |
72,30 |
80,38 |
m |
94,21222 |
84,35455 |
75,88455 |
64,71545 |
72,23889 |
80,29222 |
s |
0,054032 |
0,037779 |
0,053547 |
0,067877 |
0,031402 |
0,066479 |
</div>
gdzie: m - wartość średnia danej długości (suma pomiarów / ilość pomiarów)
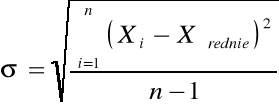
s - błąd średni kwadratowy wyliczany z następującego wzoru:
gdzie: i - numer pomiaru
n - całkowita ilość pomiarów
Xi - wartość i - tego pomiaru
Xśr - wartość średnia z n - pomiarów
Z kratek wykreskowanych usunięto błędy grube, które zwiększały średni błąd kwadratowy do wartości wyższej niż 0,07 mm (dopuszczalny błąd pomiaru wynikający z klasy przyrządu wynosi 0,03 mm).
Analogiczne obliczenia pola trójkąta, ale ze wzoru Herona:
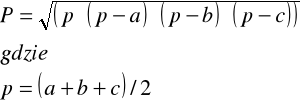
Gdzie: a, b, c - boki trójkąta
numer |
Pa |
Pb |
Pc |
Ph |
1 |
3048,901 |
3046,783 |
3040,848 |
3038,547 |
2 |
3051,4 |
3047,866 |
------------------------ |
3042,288 |
3 |
------------------------ |
3043,652 |
3043,481 |
------------------------ |
4 |
------------------------ |
3043,652 |
3043,481 |
------------------------ |
5 |
3047,341 |
------------------------ |
------------------------ |
3037,543 |
6 |
3058,768 |
------------------------ |
3054,125 |
3047,815 |
7 |
3048,312 |
3048,228 |
3048,524 |
3041,486 |
8 |
3045,134 |
3045,096 |
3043,08 |
3037,909 |
9 |
3049,901 |
3048,649 |
3048,881 |
3041,477 |
10 |
3047,37 |
3045,818 |
3047,363 |
3040,646 |
11 |
3047,37 |
3051,06 |
3050,421 |
3042,007 |
m |
3049,389 |
3046,756 |
3046,689 |
3041,08 |
s |
3,938767 |
2,460201 |
4,265664 |
3,105928 |
Gdzie analogicznie do poprzedniej metody:
m - wartość średnia danej długości (suma pomiarów / ilość pomiarów)
s - błąd średni kwadratowy
IV WNIOSKI:
W ćwiczeniu tym jedyne błędy jakie mogły się pojawić to błąd urządzenia (wynikający z rozregulowania) oraz przede wszystkim błąd wynikający z czynnika ludzkiego: niedokładne wyzerowanie suwmiarki i błąd pomiaru - ten ostatni miał największy wpływ na opracowywane wyniki.
Wzorem, na dokładność wyniku którego błąd pomiaru ma mniejszy wpływ, przy obliczaniu pól danych trójkątów, miał być wzór Herona (ze względu na duże uśrednianie cząstkowych sum) jednak widać, że tak nie jest - najprawdopodobniej z winy mierzących.
4
![]()
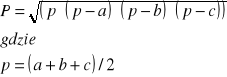
Wyszukiwarka
