EAIiE	Szadkowski Paweł Sypiański Radosław			Rok I-wszy		Grupa IV		Zespół 6
Laboratorium Fizyczne	Temat : Przerwa energetyczna w germanie							Nr ćw. 122
Data wykonania: 20.05.99	Data oddania: 26.05.99	Zwrot do poprawy :	Data odbioru:		Data zaliczenia:		Ocena :

Cel ćwiczenia:

Wyznaczenie szerokości przerwy energetycznej przez pomiar zależności oporu monokryształu germanu od temperatury.

Wprowadzenie:

Półprzewodnikami nazywamy grupę materiałów, które w temperaturze bliskiej zera bezwzględnego są izolatorami, natomiast w wyższych temperaturach posiadają wartość przewodności pośredniej między metalami i izolatorami.

Wykres poziomów energetycznych półprzewodnika, podobnie zresztą jak i izolatora, charakteryzuje obecność przerwy energetycznej, to znaczy przedziału energii, którego nie mogą zajmować elektrony.

Przerwa energetyczna oddziela pasmo walencyjne (w niskich temperaturach całkowicie wypełnione przez elektrony) od pustego pasma przewodnictwa. W przeciwieństwie do izolatora, w półprzewodnikach szerokość przerwy energetycznej
jest mała. Ze wzrostem temperatury część elektronów zostaje wzbudzona do pasma przewodnictwa i staje się elektronami swobodnymi. W paśmie walencyjnym powstaje zatem taka sama liczba dodatnich nośników prądu - dziur.

Postarajmy się teraz, opierając się na najprostszych pojęciach teorii pasmowej, wprowadzić zależność koncentracji elektronów swobodnych
i dziur
od temperatury dla półprzewodnika samoistnego (bez domieszek).

Z obliczeń opartych na modelu elektronów swobodnych wynika, że gęstość stanów (liczba stanów w przedziale energii
) jest pierwiastkową funkcją energii, liczonej od dna pasma przewodnictwa względnie wierzchołka pasma walencyjnego.

Prawdopodobieństwo obsadzenia stanu przez elektron podaje funkcja rozkładu Fermiego-Diraca

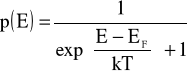
W naszym uproszczonym modelu, w którym pasmo walencyjne jest symetrycznym odbiciem pasma przewodnictwa, poziom Fermiego
znajduje się w połowie szerokości przerwy energetycznej. Liczba elektronów w przedziale energii
jest więc równa
. Całkowitą liczbę elektronów swobodnych można obliczyć przez scałkowanie tej wielkości po całej szerokości pasma przewodnictwa

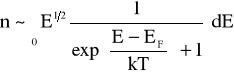
Dla zwykłych przewodników
, dlatego w powyższym wzorze jedynkę w mianowniku można pominąć, co umożliwia obliczenie całki metodą podstawiania

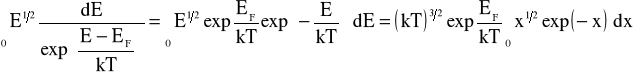
Wyrażenie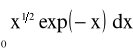
stanowi pewną liczbę rzeczywistą, której nie będziemy obliczać, gdyż wpływa ona tylko na nieznany współczynnik proporcjonalności. Jeżeli za zero energii przyjęliśmy dno pasma przewodnictwa, to
, gdzie
jest szerokością przerwy energetycznej. Zależność koncentracji nośników od temperatury przybiera zatem postać

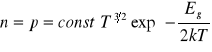
Przewodność właściwa półprzewodnika jest określona wzorem

gdzie
oznacza ładunek elementarny, a
i
- odpowiednio ruchliwość elektronów i dziur.

Przewodnictwo zmienia się z temperaturą zarówno na skutek wzrostu liczby nośników prądu, jak i zmiany ich ruchliwości.

Ruchliwość nośników w półprzewodnikach, podobnie jak w metalach, maleje ze wzrostem temperatury w wyniku oddziaływania z drganiami sieci krystalicznej. Spadek ruchliwości prawie całkowicie kompensuje czynnik
we wzorze na zależność koncentracji nośników od temperatury i w rezultacie temperaturowa zależność przewodności właściwej względnie oporu elektrycznego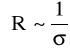
jest

opisana przez czynnik wykładniczy

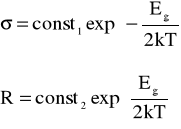
W celu uzyskania wartości E_g wyniki pomiarów oporności monokryształu germanu w funkcji temperatury przedstawiamy w formie

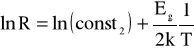
Wykres zależności
w funkcji
przedstawia prostą, której współczynnik nachylenia a jest proporcjonalny do szerokości przerwy energetycznej

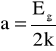
Wyniki pomiarów :

Temperatura [°C]	Oporność [Ω]
		German	Termistor
24	431,8	352,1
30	355,7	256,7
35	296,8	207,7
40	245,5	170,3
45	201,3	140,2
50	167,0	117,4
55	137,0	98,7
60	115,6	85,0
65	96,7	72,2
70	77,6	57,9
75	64,9	49,0
80	53,6	41,2
85	44,8	34,9
90	37,4	29,3
95	30,8	25,2

Opracowanie wyników :

Współrzędne punktów doświadczalnych naniesionych na wykresie zawarte są w tabeli:

1/T [1/K]	ln R ( german )	ln R ( termistor )
0,00337	6,0680	5,8639
0,00330	5,8741	5,5479
0,00325	5,6931	5,3361
0,00319	5,5033	5,1376
0,00314	5,3048	4,9431
0,00310	5,1180	4,7656
0,00305	4,9200	4,5921
0,00300	4,7501	4,4427
0,00296	4,5716	4,2794
0,00292	4,3516	4,0587
0,00287	4,1728	3,8918
0,00283	3,9815	3,7184
0,00279	3,8022	3,5525
0,00275	3,6217	3,3776
0,00272	3,4275	3,2268

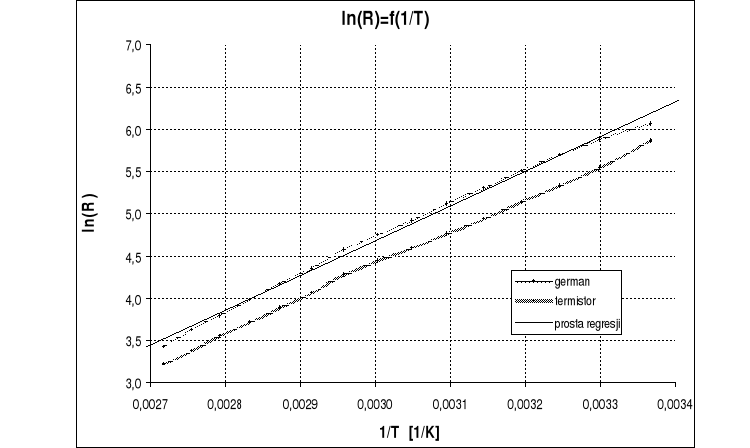
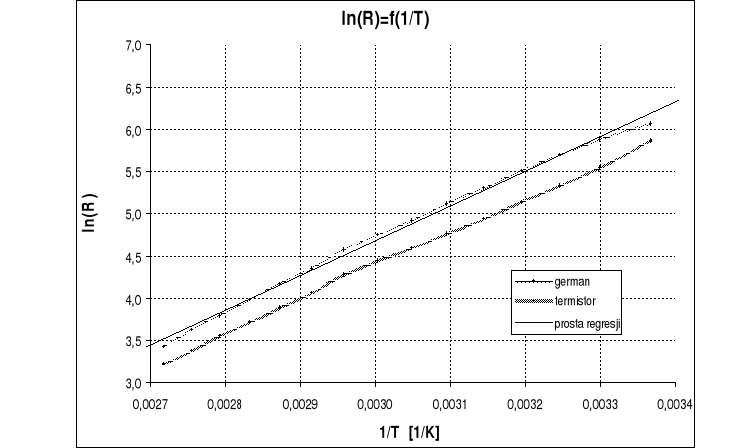
Metodą najmniejszych kwadratów została wyznaczona prosta regresji.

Współczynniki a i b do prostej zostały wyznaczone na podstawie wzorów:

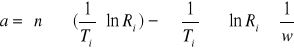
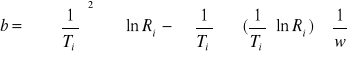
gdzie :

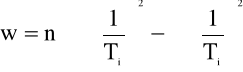
Po podstawieniu danych liczbowych uzyskaliśmy następujące współczynniki:

a = 4109,2

b = -7,651

Wykresy zależności ln(R)=f(1/T) dla germanu i termistora oraz prosta regresji :

Natomiast błędy współczynników a i b zostały wyznaczone na podstawie wzorów:

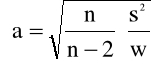
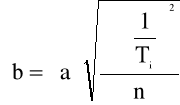
gdzie

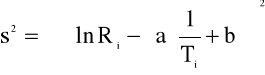
Po podstawieniu danych liczbowych otrzymujemy:

czyli

a = 4109,2 ±0,2

b = -7,651 ±0,003

Zatem prosta regresji ma równanie:

Wartość przerwy energetycznej w germanie wyznaczona została z zależności

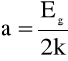
Z powyższego wzoru wynika, że przerwa energetyczna w germanie wynosi

gdzie

k - stała Boltzmana = 1,380·10^-23 [J·K^-1]

Czyli po wstawieniu danych liczbowych

E_g = ( 1,13414 ± 0,00006 ) ⋅10^-19 [J]

Wnioski :

Wykres ln(R)=f(1/T) dla germanu, który otrzymaliśmy jest prawie prosty czyli bardzo zbliżony do wykresu teoretycznego.

Widzimy również, że wykres ln(R)=f(1/T) dla termistora jest bardzo podobny do wykresu dla germanu z tym że przesunięty jest na osi ln(R) o pewną stałą wartość co może sugerować że termistor jest zbudowany właśnie z germanu ( możliwe że inaczej domieszkowanego, co mogłoby powodować powstałą odchyłkę ).

1

5