CABAN Piotr A-51 25.10.10
Rozwiązania zadań z wykładu pierwszego
TREŚĆ ZADANIA A3:
3. Równanie ruchu ma taką samą postać moment bezwładności taką samą wartość jak w poprzednim zadaniu. Jednakże
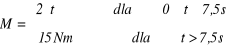
gdzie moment M wyrażony jest w Nm, gdy czas t jest podstawiony jest w sekundach. Rozwiązać równanie ruchu dla obydwu warunków początkowych podanych w poprzednim zadaniu. Narysować wykresy funkcji α(t) oraz ω(t).
W przedziale 0 ≤ t ≤7,5s równanie ruchu ma postać ![]()
. Należy je rozwiązać. Będąca rozwiązaniem funkcja α(t) powinna być parabolą trzeciego stopnia, funkcja ω(t) - parabola drugiego stopnia. Należy obliczyć wartości α i ω dla t = 7,5 s. W przedziale t > 7,5 równanie ruchu ma postać jak w zadaniu A2. Wartości α i ω dla t = 7,5 s należy wykorzystać jako warunki początkowe rozwiązania dla t > 7,5 s. Wykonując wykres w Excelu należy zadbać aby program „znał” wartości α i ω dla t = 7,5 s. Jeżeli w tablicy Excela wartości te zostaną pominięte, to na wykresach pojawią się niczym nie uzasadnione skoki.
ROZWIĄZANIE:
a- kąt obrotu |
w- prędkość kątowa |
M=15[Nm]- moment siły |
J=10 [kg*m^2] - moment bezwładności |
t- czas |
1) Dla 0 ≤ t ≤ 7,5s dane jest rówanie:
![]()
, dla zgodności jednostek do równania `dokładam' stałą x=1[Nm/s]:
![]()
Liczę całki po czasie, gdzie J i x to stałe:
![]()
, co daje:
![]()
wiedząc, że ![]()
to: ![]()
, następnie:
![]()
i ostatecznie:
![]()
Z warunków początkowych (dla t=0, a=0, w=0) wiemy, ze c1 i c2 równe są zero, wiec:
![]()
oraz ![]()
Dla t=7,5[s]:
![]()
![]()
2) Dla t>7,5s dane jest rówanie:
![]()
Liczę całki po czasie, gdzie J i M to stałe:
![]()
, co daje:
![]()
, wiedząc, że ![]()
to: ![]()
, następnie:
![]()
i ostatecznie:
![]()
Gdzie warunkami początkowymi ruchu są warunki końcowe ruchu dla 0 ≤ t ≤ 7,5s, czyli:
![]()
oraz ![]()
Dla t=15[s] (suma 7,5s ruchu dla M=2t oraz 7,5s ruchu dla M=15Nm):
![]()
![]()
WYKRESY:
2
Wyszukiwarka