1. PRZEDMIOT BADAŃ OPERACYJNYCH - MATEMATYCZNY MODEL DECYZYJNY I ETAPY JEGO BUDOWY.

1. Badania operacyjne - to naukowa metoda rozwiązywania problemów z zakresu podejmowania decyzji kierowniczych.

2. Geneza badań operacyjnych

Skojarzenie z nauką o zarządzeniu. Matematyczny opis wspieraniu kierowników w ich decyzjach. Bazuje na metodach ilościowych.

3. Pole zastosowań badań operacyjnych obejmuje:

1. sporządzenie matematycznych i statystycznych modeli decyzyjnych i modeli sterowania w celu analizy sytuacji charakteryzujących się dużą złożonością i niepewnością

2. analiza przyszłych konsekwencji wyboru decyzji i formułowanie odpowiednich mierników efektywności w celu oszacowania wartości alternatywnych rozwiązań.

4. Przykłady zagadnień, do których stosuje się badania operacyjne:

1. planowanie produkcji i zapasów

2. problemu optymalnych przydziałów (m.in. zagadnienie transportowe, zagadnienie optymalnego rozmieszczenia pracowników czy zagadnienie optymalnego przydziału maszyn)

3. planowanie eksploatacji i remontów urządzeń

4. optymalizacja mieszanek (w tym zagadnienie diety)

5. optymalizacja procesów technologicznych (w tym minimalizacja odpadów czy minimalizacja zanieczyszczeń)

6. planowanie inwestycji

5. Cechy charakterystyczne badań operacyjnych:

1. ukierunkowanie na podejmowanie decyzji

2. możliwość oceny działania na podstawie kryteriów ekonomicznej efektywności

3. zaufanie do modelu matematycznego

4. konieczność stosowania elektronicznej techniki obliczeniowej.

6. Etapy budowy modeli optymalizacyjnych w ekonomii:

1. Sformułowanie celu działania (kryterium optymalizacji), określenie zmiennych decyzyjnych i dobór parametrów strukturalnych.

2. Budowa modelu rzeczywistej sytuacji decyzyjnej - wybór typu modelu (deterministyczny, stochastyczny, strategiczny) i jego postaci analitycznej (liniowy, nieliniowy), sformułowanie warunków zadania i funkcji celu

3. Rozwiązanie modelu czyli wyznaczenie optymalnej strategii decydenta. Wykorzystujemy w tym celu różne metody w zależności rodzaju modelu:

1. programowanie liniowe

2. programowanie nieliniowe

3. programowanie cało liczbowe

4. programowanie dynamiczne

5. programowanie sieciowe

6. teorię gier

7. teorię kolejek (teorię masowej obsługi)

8. teorię odnowy i wymiany urządzeń

9. programowanie zapasów

10. programowanie wielko kryterialne

D. weryfikacja (badanie przydatności) modelu i jego rozwiązania, a w szczególności uzyskanie odpowiedzi na pytania:

• Czy model odpowiada analizowanej sytuacji decyzyjnej?

• Czy jego rozwiązanie jest zgodne z aspiracjami decydenta?

• Jaka jest wrażliwość rozwiązania na zmiany warunków zadania?

E. Wdrożenie wyników badań i doskonalenie modelu.

7. Reguły decyzyjne w metodzie simpleks z maksymalizowaną funkcją celu:

Załóżmy, że dla każdego i=1,2,...m oraz dla każdego j=m+1, m+2,...n obliczyliśmy współczynniki kombinacji liniowych z_ij oraz wskaźniki optymalności Δ_j. Wówczas może mieć miejsce jeden z trzech przypadków:

1. Jeżeli Δ_j≥ 0 dla j=m+1, m+2, ...n, to wartość funkcji celu nie może być zwiększona i plan początkowy jest optymalny.

2. Jeżeli Δ_j≤0 dla pewnego j i wszystkie odpowiadające temu indeksowi wielkości z_ij są niedodatnie (z_ij ≤ 0, i=1,2...m), to funkcja celu zadania jest nieograniczona na zbiorze rozwiązań dopuszczalnych i zadanie nie posiada rozwiązania.

3. Jeżeli Δ_j< 0 i dla każdego takiego j co najmniej jedna z liczb z_ij jest dodatnia, wówczas rozwiązanie można ulepszyć.

W przypadku minimalizowanej funkcji celu znaki przy wskaźnikach optymalności zmieniamy na przeciwne - możemy ulepszyć rozwiązanie, jeżeli istnieją dodatnie wskaźniki optymalności dla pewnych j i dla każdego takiego j co najmniej jedna z liczb z_ij jest dodatnia.

8. Podstawowe twierdzenia dotyczące rozwiązań liniowych modeli decyzyjnych:

Twierdzenie 1. Zbiór rozwiązań dopuszczalnych zadania programowania liniowego jest wielościennym zbiorem wypukłym.

Twierdzenie 2. Jeśli istnieje optymalne rozwiązanie zadania programowania liniowego, to istnieje przynajmniej jedno optymalne rozwiązanie wierzchołkowe (bazowe) tego zadania.

Twierdzenie 3. Jeśli istnieją dwa optymalne rozwiązania danego zadania programowania liniowego, to dowolna wypukła kombinacja liniowa tych rozwiązań jest również optymalnym rozwiązaniem zadania.

9. MATEMATYCZNY MODEL DECYZYJNY - jest to opis sytuacji decyzyjnej w języku matematyki

Elementy:

1. zmienne decyzyjne: x₁, ..... x_n

2. parametry a, b, c.

Parametry są to dane wielkości. Zmienne - wielkości które należy ustalić, stałe elementy decyzyjne. Funkcja celu (funkcja kryterium) - funkcja, która mierzy cel jaki chce osiągnąć decydent (np. max, zysk, min kosztów)

Ograniczenia - opis sytuacji decyzyjnej:

• ograniczenia:

• warunki wewnętrzne zgodności (warunki uboczne) - układ równań lub nierówności

• warunki brzegowe (dodatkowe) - nakładają na zmienne pewne dodatkowe warunki

Funkcja celu -> L(x)

1. MODELE PROGRAMOWANIA LINIOWEGO (PL)

Model PL gdzie funkcja celu jak i wszystkie warunki wewnętrznej zgodności są liniowe, a jedynym warunkiem brzegowym jest założenie o nieujemności zmiennych decyzyjnych

• dwa warianty modelu:

1. zasada racjonalnego gospodarowania - max efektów działań lub min kosztów

• postać standardowa modelu PL

x₁, x₂, x₃ -> zmienne decyzyjne

L(x) = c₁x₁ + c₂x₂+...+c_nx_n -> max

Warunki wewnętrznej zgodności:

a₁₁x₁+a₁₂x₂+a_1nx_n≤b₁

a₂₁x₁+a₂₂x₂+a_2nx_n≤b₂

a_n1x₁+a_n2x₂+a_nnx_n≤b_n

warunki brzegowe:

Y₁…..x_n ≥0

a_ij -> norma zużycia i - tego czynnika produkcji przy produkcji jednostki j - tego wyrobu

b - ograniczone zasoby czynników produkcji.

1. wariant drugi:

L(x) = c₁x₁ + c₂x₂+...+c_nx_n -> min

a₁₁x₁+a₁₂x₂+a_1nx_n≥b₁

a₂₁x₁+a₂₂x₂+a_2nx_n≥b₂

a_n1x₁+a_n2x₂+a_nnx_n≥b_n

a_ij - zawartość I - tego składnika odżywczego w jednostce j - tego produktu.

1. Metoda geometryczna rozwiązywania zadań PL

Stosujemy gdy mamy 2 zmienne decyzyjne, wykreślanie nierówności na płaszczyźnie.

Twierdzenie 1. Zbiór rozwiązań dopuszczalnych (decyzja możliwa do podjęcia, układ wartości zmiennych decyzyjnych, który spełnia wszystkie ograniczenia (wielościenny zbiór wypukły - wraz z 2 punktami, odcinek)

Twierdzenie 2. Rozwiązanie optymalne jest to najlepsze rozwiązanie spośród rozwiązań dopuszczalnych. Może być 1 rozwiązanie optymalne lub wcale. Optymalne rozwiązanie należy szukać na wierzchołku.

Twierdzenie 3. Jeżeli istnieją 2 optymalne rozwiązania danego zadania programowania liniowego to dowolna wypukła kombinacja liniowa tych rozwiązań liniowych jest również optymalnym rozwiązaniem zadania.

2. Metoda gradientu.

Graficzna metoda wyznaczania wierzchołka optymalnego. Gradient -> wektor pochodny cząstkowy (funkcji celu), wyznacza kierunek najszybszego wzrostu funkcji celu.

Metoda ta polega na tym, że rzutujemy prostopadle wierzchołki na gradient. Ten który znajduje się najwięcej na gradiencie jest optymalny.

3. Postać kanoniczna modelu PL

Wszystkie warunki wew. zgodności są równościami. Zamiany nierówności i równości.

1. Wprowadzenie dodatkowych zmiennych lub odjęcie jeśli ≤ to aby uzyskać = to do lewej strony dodajemy zmienne, jeśli ≥ to dodatkowe zmienne odejmujemy. Każda nierówność to jedna (inna) dodatkowa zmienna Dodatkowe zmienne (swobodna, uzupełniająca)

2. Rozwiązanie bazowe: To rozwiązanie, które powstaje przez przyjęcie, że n-m zm.=0, i rozwiązanie układu równań Ax=B

3. Rozwiązanie podstawowe: Nieujemne rozwiązanie bazowe, czyli takie rozwiązanie dopuszczalne, w którym występuje co najmniej m dodatnich wartości x_j.

4. Metoda algebraiczna - rozwiązywania zadania PL. Polega na pełnym przeglądzie zbiorów rozwiązań bazowych.

1. Metoda SIMPLEKS.

Ukierunkowany przegląd zbioru rozwiązań bazowych. Wychodzimy od pewnego rozwiązania podstawowego i je ulepszamy, tzn. przechodzimy do coraz to lepszych bądź nie gorszych rozwiązań podstawowych tym przeglądzie pomijamy wszystkie bazowe rozwiązania bazowe niedopuszczalne oraz gorsze od już znalezionych.

Wzór na ulepszenie rozwiązania:
, dla każdego i=1,2,.....m

Wzór na wskaźnik optymalności:


Nowa wartość funkcji celu:
Rozwiązanie jest lepsze gdy Δ_j jest ujemna.

Gdy wskaźnik nie jest optymalny (bo jest ujemny), więc x₁ nie jest optymalne, więc należy ulepszać.

2. Algorytm simpleks.

Jest to formuła tablicowa metody simpleks. W algorytmie simpleks wychodzimy od najgorszego rozwiązania podstawowego, tj takiego w którym przyjmujemy, że zmienne decyzyjne są = 0.

c_i - współczynnik funkcji celu przy zmiennych bazowych

c_j - współczynnik funkcji celu przy wszystkich zmiennych.

Wektory bazy - kolumny macierzy A stojące przy zmiennych bazowych

B - w pierwszej tablicy wyrazy wolne w warunkach ubocznych i jednocześnie pierwsze rozwiązanie podstawowe, a w każdej dalszej tablicy aktualnie rozwiązanie podstawowe.

A - kolumna macierzy A







3. Rozwiązania można ulepszyć gdy delty są ujemne.

Ulepszając tablicę simpleks:

1. wybieramy kolumnę kluczową -> wskazuje zmienna wprowadzoną do bazy (wybieramy tę, która ma najmniejszą ujemną wartość wskaźnika delta, gwarantuje nam najszybszy wzrost wartości funkcji celu

2. wiersz kluczowy -> wskazuje zmienną która opuszcza bazę, czyli ta która się wyzerowuje, aby to zrobić należy wyliczyć
   

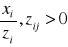
3. Na przecięciu wiersza kluczowego i kolumny kluczowej znajduje się element rozwiązujący

4. reguły przekształcania tablicy simpleks:

1. elementy wiersza kluczowego dzielimy przez element rozwiązujący

2. pozostałe elementy uzyskujemy wg. wzoru, nowy element to będzie:
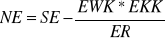
   , EWK - element wiersza kluczowego, EKK - element kolumny kluczowej, ER - element rozwiązujący, NE - nowy element, SE - stary element

5. Metoda sztucznej bazy (metoda M)

Metoda sztucznej bazy jest rozwinięciem algorytmu simpleks na przypadek, gdy występuje problem ze znalezieniem pierwszego rozwiązania podstawowego, tzn. wówczas gdy w postaci standardowej zadania występują warunki typu „≥” bądź „=”.

W metodzie tej do każdego warunku, który w postaci standardowej był typu „≥” bądź „=” dodajemy po jednej zmiennej SZTUCZNEJ. Modyfikujemy również funkcję celu: jeśli funkcja jest maksymalizowana to odejmujemy od niej sumę zmiennych sztucznych ze współczynnikiem M a jeśli jest minimalizowana to dodajemy sumę zmiennych sztucznych ze współczynnikiem .

Jeśli wyjściowe zadanie jest niesprzeczne to w optymalnym rozwiązaniu zadania ze zmiennymi sztucznymi (zadania rozszerzonego) wszystkie zmienne sztuczne się wyzerują.

6. Zagadnienie transportowe a kryterium kosztów.

Zakładamy, że mamy m - dostawców jednorodnego towaru w ilościach a₁, a₂,....a_m, mamy n - odbiorców tego towaru, których zapotrzebowanie wynosi b₁,b₂....b_n. Dodatkową informację wielkości c_ij - jednostka koszty transportu na trasie od i - tego dostawcy do j- tego odbiorcy.

x_ij - > wielkość przewozu ładunku na trasie od i -tego dostawcy do j - tego odbiorcy





-> jeśli tak jest, to zadanie transportowe ZBILANSOWANE, może być inaczej, czyli „>” to zadanie otwarte, NIEZBLINASOWANE, jeśli jest „=” to warunki uboczne bez zmian





, x_ij≥0 dla i=1,2.....m, j=1,2.....n -> jest to program liniowy

7. Algorytm Hitchocka

Ilość zmiennych nxm, warunki m+n, ilość niezerowych wartości będzie miało rozwiązanie bazowe -> m+n-1

Niezdegenerowane rozwiązanie bazowe zagadnienia transportowego ma dokładnie m+n-1 niezerowych przepływów x_ij, jeśli jest zdegenerowane to mniej niż m+n-1 (bo więcej 0). Żeby zbilansować to zadanie należy dopisać fikcyjnego odbiorcę, który koszty transportu ma równe 0.

8. Etapy algorytmy Hitchocka

1. opracowanie planu początkowego:

• metoda lewego górnego rogu (metoda kąta pn. zachodniego)

• metoda minimum macierzy

b. badanie optymalności i ulepszenie planu początkowego, plan początkowy -> wpisujemy max możliwy przepływ.

9. Metoda minimum macierzy

W tej metodzie wpisujemy maksymalny możliwy przepływ w miejsce z najmniejszym kosztem jednostkowym. (wykreślamy - kolumnę - przydział ładunku zaspokajający popyt odbiorcy, wiersz - wiersz jeśli przydział ładunku zaspokaja całą podaż dostawcy), Dalej w następne miejsce z max możliwy przepływ itd....

Plan niezdegenerowany to jeśli ma więcej niż 7 przepływów.

Wskaźniki optymalności:
, c_ij - jednostkowe koszty transportu, c_ij - koszty pośrednie.

Plan początkowy jest optymalny jeśli wszystkie wskaźniki optymalności są niedodatnie, czyli Δ_ij≤0. Plan początkowy można ulepszyć jeśli istnieją jakieś dodatnie wskaźniki delta ij.

Koszty pośrednie - metody liczenia:

1. metoda różnic

2. metoda potencjałów

Metoda różnic - należy tu jako koszty pośrednie dla wszystkich niezerowych tras jako koszty pośrednie przyjmujemy koszty bezpośrednie (jednostkowy koszty transportowe), (koszty pośrednie mogą być ujemne). Metoda ta opiera się na obserwacji, że różnice między elementami dwóch dowolnych kolumn lub wierszy są stałe. Gdy występują dodatnie wartości to nie jest dobry.

Metoda potencjałów - wypisujemy koszty transportowe gdzie nie są zerowe przepływy, a następnie wprowadzamy pomocnicze zmienne u₁, u₂, u₃...., v₁...v₂. Pozostałe koszty pośrednie otrzymane sumując pozostałe ulepszenie planu początkowego, bo nie jest optymalny (wprowadzamy jedną nową trasę, a jedną likwidujemy). Wprowadzamy do bazy trasę z największą wartością wskaźnika optymalności.

Plan początkowy ulepszamy wpisują znak + w miejscu z największa delta, a następnie wytyczamy obwód zamknięty wstawiając na przemian znaki „-„ i „+”. Jako wartość Θ wielkość ładunku na nowej trasie, jako Θ przyjmujemy najmniejszą z liczb oznaczoną znakiem „-„ i następnie zgodnie z oznaczeniem „+” lub „-„.

K₂=K₁- ΘΔ_ij

Δ_ij - jednostkowe zyski na transporcie wynikające z uruchomienia danej trasy.

10. Twierdzenia o zagadnieniu transportowym.

Twierdzenie 1. Zagadnienie transportowe w którym łączna objętość dostaw jest równa łącznej objętości zapotrzebowania, posiada rozwiązania.

Twierdzenie 2. Jeżeli wielkość dostaw i zapotrzebowania zadania transportowego wyrażają się liczbami całkowitymi, to optymalne rozwiązanie tego zadania jest również całkowitoliczbowe.

Twierdzenie 3. Aby zadanie transportowe było niezdegenerowane potrzeba i wystarcza, aby nie było takiej niepełnej grupy punktów dostawcy, dla której łączna objętość dostarczonego produktu równa się sumarycznemu zapotrzebowaniu pewnej grupy punktów odbioru.

11. Zagadnienie transportowo - produkcyjne

Zakładamy, że nasi dostawy są producentami, koszty transportu i produkcji możemy liczyć razem.


, c_ij -> jednostkowe koszty transportu na każdej z tras, p_i -> jednostkowe koszty produkcji u każdego z producentów:



, j=1,2....n -> zaspokojeniu popytu każdego z odbiorców


,-> zdolność produkcyjna dostawcy (producenta)

Przekształcając tablicę kosztów jednostkowych, do kosztów transportowych dodajemy koszty produkcji. C^*=[c_ij^*] -> macierz łącznych kosztów jednostkowych transportu i produkcji (trzeba wprowadzić fikcyjnego odbiorcę, który reprezentuje niewykorzystane zdolności produkcyjne).

12. Zagadnienie transportowo - magazynowe


-> podaż przekraczająca popyt, c_ij -> jednostkowe koszty transportu, m_i - > jednostkowe koszty magazynowania (to co niewywiezione to magazynowane).

Zagadnienie transportowe magazynowe polega na ustaleniu takich tras przewozu, które będą minimalnym kosztem transportu i kosztu magazynowania.

Funkcja celu:
, Wprowadzamy fikcyjnego odbiorcę, n+1 będzie reprezentował magazyny u dostawców.

13. Dualizm w programowaniu liniowym

Twierdzenia o dualizmie:

Twierdzenie 1. Dla dowolnych rozwiązań dopuszczalnych programu pierwotnego i programu dualnego zachodzi


Twierdzenie 2. Jeśli oba programy sprzężone posiadają rozwiązania optymalne x^o i y^o to są takie i tylko takie rozwiązania dla których wartości funkcji celu są sobie równe tj. L(x^o)=K(y^o)

Twierdzenie 3 (O komplementarności) Rozwiązania dopuszczalne x^o i y^o programów pierwotnego i dualnego są rozwiązaniami optymalnymi tych programów wtedy i tylko wtedy gdy dla każdego i=1,...m oraz j=1...n zachodzi





WNIOSEK: Jeżeli rozwiązanie optymalne jednego z programów spełnia pewien warunek uboczny z ostrą nierównością, to odpowiadająca mu zmienna zadania sprzężonego przyjmuje w rozwiązaniu optymalnym wartość równą 0.

Etapy:

1. programy sprężone mają to, że jeśli znamy rozwiązanie jedno to znamy też drugie

2. Program będzie miał zmienne programu dualnego -> tyle zmiennych ile jest warunków i odwrotnie, ile jest w programie pierwotnym

3. Funkcja celu z max przechodzi na min lub odwrotnie

4. Parametry funkcji celu PD są ograniczeniami w warunkach ubocznych PP i odwrotnie.

5. Znaki nierówności zamieniamy na przeciwne

6. Macierz współczynników a_ij w warunkach ubocznych jest transpozycja macierzy współczynników PP

7. Tyko wtedy gdy ≤ to stosujemy PD, jeśli będzie ≥ to mnożymy przez -1, jeśli = to zamieniamy ≤,≥ i jedno przez -1.

Optymalne wartości zmiennych dualnych odczytamy jako wartości bezwzględne, wskaźniki optymalnych dla zmiennych swobodnych w optymalnej tablicy simplex.

1. Interpretacja dla wyjściowej sytuacji decyzyjnej.

Optymalne wartości zmiennych dualnych są to krańcowe efektywności środków produkcji, tzn. mówią one nam o ile wzrośnie funkcja celu jeśli zwiększymy limit danego środka produkcji o jednostkę.

2. Programy nieliniowe

1. metoda mnożnika Langrange'a - stosowane dla nieliniowych programów w postaci kanonicznej

2. Metoda (twierdzenie) Kuhna - Tuckera - stosowane dla nieliniowych programów w postaci standardowej.

Obie te metody mają zastosowanie do rozwiązywania zadań programowania wypukłego, tj. zadań w których maksymalną wklęsłą lub minimalną wypukłą funkcją celu a zbiór rozwiązań dopuszczalnych jest wypukły.

Funkcja f jest ściśle wypukła bądź ściśle wklęsła, jeżeli w zależnościach nierówności nieostre zostaną zastąpione nierównościami ostrymi.

Twierdzenie 1. Warunkiem koniecznym tego, aby w punkt x^o istniało ekstremum funkcji f przy danych warunkach jest zerowanie się różniczki zupełnej rzędu jeden funkcji Lagrange'a.

Twierdzenie 2. Funkcja f osiąga w punkt x^o spełniającym warunek 1 min (max) warunkowo, jeśli różniczka zupełna rzędu dla funkcji Lagrange'a a względem wektora x.

3. Analiza portfelowa.

Analiza portfelowa dotyczy analizy na giełdzie. Optymalizacja portfelowa A i B (akcje) w jakich proporcjach kupować A i B

Seria 30
1. Firma z Saint Louis z MSI wartym opisania w książce Kaczmara - Monsanto /str 29

2. Ile biedni Polacy wydali na badania w 99 (gówno mnie to w sumie obchodzi) - 250 mln zł

3. Graficzna forma prezentacji wyników analiz służy do ilustracji wielkości względnych lub skumulowanych - Histogram /str 320

4. Pytanie o funkcję wykładniczą rosnącą / str 308

5. Kolorowe kwestionariusze i test chi-kwadrat / str. 290 i tu chyba jakieś zadanko parchate

6. Tabulacja dwudzielna w której dane z odpowiedzi nierozłącznych krzyżują się z danymi z odpowiedzi rozłącznych jest charakterystyczna dl pomiaru - nominalnego albo przedziałowego

7. Model czynnikowy - eksperyment statystyczny / str 239

8. Instrument pomiaru w obserwacji uczestniczącej - dziennik obserwacji / str 229

9. Badacz aby coś zbadać musi określić obiekt. Opis obiektu w języku etnicznym - definicja /str 73 chyba

10. W konstruowaniu problemu decyzyjnego badacz musi określić dokładnie sytuację. Pomaga mu w tym - analiza informacji uzyskanych od decydentów / str 49

11. Badacz budując kwestionariusz najpierw musi określić niezbędność pytań, ilość i zakres, bezpośredniość. Kolejna czynność to sprawdzenie czy - respondent jest zdolny udzielić dokładnej odpowiedzi. / 3 to skłonność do odpowiedzi. Str 100

12. Najprostsza ze skal złożonych pomiaru postaw to - skala pozycyjna / str 123

13. Kto wydaje ( a kogo normalnego to obchodzi?) „Statistics and Economics” - Euromonitor

14. Pocztą elektroniczną lub pisemnie odpowiada się na (listy hehe) - znajdźcie sobie

15. O czym decyduje badacz po ustaleniu składu obliczonej próby - reprezentatywność

Seria 31
1. (31)W jakich pomiarach ma zastosowanie krzywa poligraficzna? I co myślicie, że w fizjologicznych - a co jeśli wszystkie są wymienione?

2. W jakich latach rozpoczęto powszechnie stosowanie komputerów w badaniach rynkowych?
/no i tego Kaczmar nie ma w swej książce wprost nigdzie. Do wyboru było: po 80 / 70-80 / 60-70 / 50-60/ 40-50/

3. Zadanie - populacja 1000, próbka 100 z czego podzielona 50/50. Jaki błąd wystąpi? /0,05

4. W jakich blebleble ma zastosowanie współczynnik alfa (Cronbacha czy coś) - metoda połówkowa

5. Jaka organizacja ma siedzibę w polsce i zrzesza badaczy rynkowych - PTBRIO czy jakoś tak - pierwsze w każdym razie

6. Jaka metoda badania popularności stron internetowych czy czegoś tam w Internecie jest stosowana a w Polsce jeszcze w powijakach? - infometria

7. Jakieś pytanie bezczelne o tabulację dwudzielną i pełno podobnych odpowiedzi.

8. Która firma (jakby tylko jedna na świecie taka była) ma wypasiony MSI ale tam to było opisane tak bardziej na okrętkę - Monsanto (czy jakoś tak)

9. Co robi badacz jak już się pokapuje, że ziom jest skłonny do odpowiedzi? - mi tam wszystko pasowało

10. Jaka informacja redukuje całkiem niepewność i ryzyko podjęcia decyzji? -doskonała

11. Pytanie o Kahna - futurolog, metoda scenariuszowa

Seria 32 okruchy
1. Reprezentanci różnych dyscyplin rozwijają niezależnie od siebie pojęcia i działania jak identyfikacja potrzeb… (SIK) nic nie czaje : -badań marketingowych

2. Błędny wynik wynikający z różnicy między danymi niezbędnymi a poszukiwanymi - błąd problemu badawczego

3. Która z podanych niżej metod doboru próby nie wymaga określenia minimalnej liczebności próby przed zebraniem danych w terenie? / ponoć wszystkie odpowiedzi są dobre

4. Jak nazywa się pojęcia w systemach dedukcyjnych, które przyjmuje się bez definicji - aksjomaty

5. Analiza mocy różnicujące to pojawia się przy babraniu się w - skali Likerta

6. Od jakich źródeł powinien zaczynać wielki badacz jak Kaczmar? -wewnętrznych wtórnych

7. Do jakiej metody zbierania danych ze źródeł pierwotnych odnosi się większość metod redukcji bbo? - ankieta pocztowa

8. ZA którą grupę metod zbierania danych ze źródeł pierwotnych odpowiedzialny jest moderator? - wywiad grupowy

9. Piardu piardu dział strategii i takich tam - 3M

10. Ile grup kontrolnych ma eksperyment dwugrupowy z serią pomiarów? - 1

11. Co nie bierze udziału przy ocenie skuteczności badań? -etyka

12. Pytanie o coś ale odpowiedź - wskaźniki natężenia

13. Średnia ruchoma - wahania sezonowe

Seria 33

1. Co następuje po wyznaczeniu dnaych do rozwiązania problemu decyzyjnego i sformułowaniu hipotez? - formułowanie problemu badawczego

2. SQI w firmie wybranej przez Kaczmara - Federal Express

3. co następuje po analizie danych? - prezentacja ustna

4. Co nie należy do zbierania danych ze źródeł pierwotnych? /czytanie przez Kaczmara pisemek w czytelni chyba wszystkie odpowiedzi mu się posrały

5. coś o terminalach - instrumenty stacjonarne (chyba)

6. Średnia ruchoma scentrowana - analiza wahań sezonowych

7. Zadanie na obliczenie chi-kwadrat

8. Zadanie na liczebność próby (wzory na ściągę!!!)

9. Firma przeprowadzająca badania lojalności pracowników - Protector (choć niektórzy twierdzą, że konsalnet ale książka mówi, że ten pierwszy)

10. Skala proporcjonalna to inaczej - skala stosunkowa (bez skojarzeń)

11. Instrukcja kwestionariusza „Jeśli skończyłeś to oddawaj kartkę i wypier…” - kierujące procesami pomiaru

12. Porównawcza i skala sumowanych ocen (?) - skala prosta

13. Wykaz produktów z odpowiadającymi im symbolami cyfrowymi z zakodowaną klasyfikacją - nomenklatura towarowa

14. Rodzaje eksperymentów, który należy do eksperymentów z wieloma zmiennymi niezależnymi? - czynnikowy

15. Coś o firmach i usługach przez nie świadczonych

SERIA I

1. Informacja jest stanem niematerialnym, nie jest ani energią, ani materią. Jej przeniesienie może odbywać się pod warunkiem, że:

1. Zostanie użyty zmysł wzroku,

2. Przybierze ona określoną postać fizyczną w formie nośnika,

3. Określi się dokładnie jej granicę występowania,

4. Zostanie przekazana przez nadawcę do adresata,

5. Wystąpi w czystej postaci poza systemem nerwowym człowieka.

2. Jeżeli wystąpi różnica między wynikami przekazanymi przez badacza a informacją odebraną przez użytkownika to jest to błąd:

1. Prezentacji wyników analizy,

2. Problemu badawczego,

3. Pomiaru,

4. Wytypowania niewłaściwej populacji generalnej,

5. Analizy danych

3. Lista odwzorowująca wszystkie elementy badanej populacji nazywa się:

1. Wykazem,

2. Operatem (losowania),

3. Zarówno operatem jak i wykazem

4. Książką adresową

5. Zupełnie inaczej.

4. Podstawowym warunkiem konstrukcji instrumentu zwłaszcza konwencjonalnego jest dostosowanie odpowiednich skal do

instrumentu, czy instrumentu do tych skal. Czynność ta nazywa się:

1. Przyporządkowanie symboli cechom obiektu,

2. Cechowaniem instrumentu,

3. Wyznaczaniem poziomu pomiaru,

4. Skalowaniem instrumentu,

5. Zarówno skalowaniem jak i wyznaczaniem poziomu pomiaru.

5. W ramach stosowanej metody odpowiedzi losowanych zadano respondentowi 2 pytania:

A-Czy kupowałeś cokolwiek w tym sklepie w ostatnim miesiącu?

B-Czy urodziłeś się w maju?

Zakładając, że mechanizm losowania jakim jest rzut monetą daje równe szanse wyboru pytania A i B,

proporcja twierdzącej odpowiedzi łącznie na dwa pytania (A i B) wyniosła 0,20,

a ze statystyk spisu powszechnego wynika, że 20% mieszkańców urodziło się w maju - proporcja twierdzącej odp na pytanie wyniosłą:

1. 20%

2. 25%

3. 30%

4. 35%

5. 40%

6. Każda składowa skali somatycznej jest zazwyczaj skalą dwubiegową z dwu stron parą:

1. Rzeczowników,

2. Antonimów,

3. Przymiotników,

4. Synonimów,

5. Wyróżników.

7. Który z wymienionych niżej czynników decyduje o wiarygodności pomiaru wtórnego?

1. Trafność,

2. Dostępność,

3. Dokładność,

4. Aktualność,

5. Jeden z wyżej wymienionych.

8. Osiągnięty ostatecznie procent odpowiedzi (70%) przez redakcję miesięcznika „Turystyka Zagraniczna” upoważnia

do wyrażenia opinii, że:

1. BBO zalicza się do bezpiecznych i nie wymaga jego oszacowania,

2. BBO mieści się co prawda w bezpiecznych granicach, ale istnieje duże ryzyko popełnienia błędu przy podejmowaniu decyzji,

3. BBO przekroczył granicę bezpieczeństwa i należy dokonać szacunków metodą próbki z próby,

4. BBO okazał się tak duży, że przekreśla całkowicie przeprowadzone badanie,

5. Należało poświęcić zdecydowanie więcej czasu na przygotowanie badania.

9. Oto przykład trzynastopozycyjnego kodu kreskowego EAN: 7 310040 013186. W podkreślonych pięciu cyfrach zakodowano:

1. Numer producenta

2. Liczbę kontrolną,

3. Kraj pochodzenia produktu

4. Cenę produktu,

5. Numer produktu.

10. Symulowany test rynkowy STM znalazł główne zastosowanie w:

1. Pomiarach efektywności oddziaływania reklamy pocztowej,

2. Ocenie pilotowego programu telewizyjnego

3. Określenia efektywności reklamy prasowej,

4. Identyfikacji reklamy produktów konkurencyjnych,

5. Testowanie najczęściej kupowanych produktów konsumpcyjnych.

11. Załóżmy, że respondent odpowiedział, iż nigdy nie słyszał o danym produkcie, podczas gdy z odpowiedzi na inne pytanie

tego samego kwestionariusza wynika, że używa on tego produktu. Błąd tego rodzaju redaktor powinien zaliczyć do:

1. Odpowiedzi nieadekwatnych,

2. Sprzeczności i niezgodności,

3. Odpowiedzi niekompletnych i niejednoznacznych,

4. Pomiarów fikcyjnych,

5. Żadnego spośród wymienionych wyżej rodzajów błędów i braków.

12) Średnia arytmetyczna może być obliczona tylko z danych uzyskanych z pomiaru:

1. Interwałowego,

2. Porządkowego,

3. Ilorazowego,

4. Zarówno jednostkowego jak i proporcjonalnego,

5. Nominalnego.

13) Grupa specjalistów będących respondentami w pomiarze metodą delfiaka nazywana jest:

1. Próbą,

2. Grupą ekspertów,

3. Grupą korespondentów,

4. Panelem,

5. Zupełnie inaczej.

14) Jak zapisałbyś liczbę 50,89 w raporcie?

1. 50,9

2. 50,89

3. 50,8

4. 51

5. 51,0

15) Które spośród niżej wymienionych grup przedsiębiorstw są jednocześnie wykonawcami badań marketingowych na zlecenie oraz zleceniodawcami tych badań:

1. firmy badawcze,

2. przedsiębiorstwa wytwarzające dobra konsumpcyjne,

3. przedsiębiorstwa handlowo-usługowe,

4. firmy świadczące usługi finansowe,

5. agencje reklamowe.

SERIA II

1. Dane o rynkach zbierano już w Średniowiecznej Europie, czego dowodem było m. in. To, że każdy z

domów bankowych dysponował własną służbą informacyjną. Działalność tych służb dała początek:

1. Rozwojowi firm badawczych,

2. Pierwszym gazetom,

3. Badaniom ankietowym,

4. Sformalizowanym badaniom marketingowym,

5. Wywiadowi gospodarczemu.

2. W ramach definiowania problemu badawczego najważniejszą wstępną czynnością badacza jest ścisłe określenie:

1. Hipotez badawczych,

2. Planu współpracy z decydentami,

3. Rodzaju pytań kwestionariuszowych,

4. problemu decyzyjnego,

5. problemów wymienionych w punktach a i c razem.

3. W praktyce istnieje pewna maksymalna ilość metod doboru losowego i nielosowego prób. Ta maksymalna liczba metod wynosi:

1. 12, b) 16, c) 32, d) 24, e) 64.

4. Czynność odwzorowania mierzonej cechy przy pomocy wybranej skali nazywa się:

1. Cechowaniem,

2. Wyznaczaniem poziomu pomiaru,

3. Symbolizowaniem,

4. Skalowaniem,

5. Pomiarem.

5. Układając pytania kwestionariuszowe należy dążyć do ich jednoznaczności. Jednoznaczność oznacza, że:

1. Odpowiedz na pytanie dostarcza ścisłych danych,

2. Pytanie jest całkowicie jasne dla respondenta,

3. Uzyskuje się dane na temat ściśle określonego zagadnienia,

4. Wszyscy respondenci rozumieją pytanie jednakowo,

5. Pytanie nie zawiera problemów drażliwych i kłopotliwych.

6. Wynikiem analizy danych zebranych przy pomocy skali somantycznej jest zwykle obraz graficzny przedstawiający

porównawczy zestaw linii nazywamy:

1. Siecią preferencji,

2. Somantyczną skalą podstaw,

3. Profilem polaryzacji,

4. Zestawem skal porządkowych.,

5. Dwuwymiarowym obrazem preferencji.

7. Problem porównywalności dostępnych danych występuje w statystykach międzynarodowych wówczas,

gdy mamy do czynienia z różnymi:

1. Wykazami statystycznymi towarów,

2. Klasyfikacjami towarowymi,

3. organizacjami i biurami statystycznymi,

4. nomenklaturami towarowymi,

5. wykazami kodów statystycznych towarów.

8. Za najbardziej efektywną metodę oszacowania błędu wynikającego z braku odpowiedzi (BBO) uważa się:

1. Metodę ekstrapolacji,

2. Metodę próbki z próby,

3. Metodę szacowania subiektywnego,

4. Metodę porównywania ze znanymi parametrami,

5. Metodę szacowania subiektywnego.

9. Oto przykład trzynastopozycyjnego kodu kreskowego EAN 7 310040 013186. W podkreślonych cyfrach zakodowano:

1. Cenę produktu,

2. Numer produktu,

3. Liczbę kontrolną,

4. Numer producenta,

5. Kraj pochodzenia produktu.

10. Jeżeli po upływie pewnego czasu część respondentów odmawia udziału w eksperymencie lub następują

inne nieprzewidziane zmiany naturalne to mówimy, że błąd spowodowany został:

1. Zmianą składu próby,

2. Wpływem czynników niekontrolowanych,

3. Reakcją respondentów,

4. Wpływem pierwszego pomiaru,

5. Łącznie zmianą składu i reakcją respondentów.

11. Poza konkretnymi metodami dokonywania poprawek i uzupełnień należy przestrzegać pewnych zasad ogólnych poprzez:

1. Konieczność przygotowania instrukcji redagowania danych, gdy zatrudnia się więcej niż jednego redaktora,

2. Upewnienie się, że kiedy przedmiot pomiaru był uwzględniony w dobranej próbie,

3. Podawanie redakcji wyników pomiarów bezpośrednio po ich zakończeniu,

4. Przydzielanie redaktorowi tych samych osób prowadzących pomiary,

5. Stosowanie wszystkich wymienionych wyżej sposobów jednocześnie.

12. Średnia arytmetyczna, mediana i dominanta różnią się między sobą w przypadku:

1. Gdy porównuje się ze sobą dwie lub więcej populacji,

2. Asymetrycznego rozkładu częstości wyników pomiaru,

3. Gdy zostaną wykreślone na jednym układzie współrzędnych,

4. Szeregów silnie asymetrycznych,

5. Dużych wartości skrajnych w danym szeregu.

13. Metody eksploatacyjne wykazują niewielkie możliwości w przewidywaniu:

1. Tempa wzrostu lub spadku,

2. Rozwoju wydarzeń w długim okresie,

3. Punktów zwrotnych, w których tempo wzrostu lub spadku gwałtownie się zmienia,

4. Rozwoju zjawisk w niestabilnych warunkach,

5. Sprzężeń zwrotnych.

14. Wzory i kopie użytych w badaniu instrumentów pomiarowych (konwencjonalnych)

najlepiej jest zaprezentować słuchaczom a wykorzystaniem:

1. Filmu,

2. Handoutu,

3. Planszy,

4. Slajdu,

5. Video taśmy.

15. Usługi badawcze polegające na zbieraniu regularnie danych na określony temat,

przetwarzanie ich i sprzedawanie zainteresowanym klientom w formie raportów lub okresowych opracowań,

zwykle na zasadzie subskrypcji (nie zlecenia) nazywane są w Stanach Zjednoczonych i Wielkiej Brytanii usługami typu:

1. Custom - designed,

2. Syndicated research (sevices),

3. Ad - hoo rsearch,

4. Full - service,

5. Information broker.

SERIA III

Jedna z definicji mówi, że “funkcją badań marketingowych” jest dostarczanie informacji, która mogłaby

wesprzeć przedsiębiorstwo w podejmowaniu decyzji. Autorami tej definicji są:

1. Zeltman i Berger,

2. Kotler,

3. Aken i Day,

4. Tull i Hawkins

5. Crisp.

2. Trafne zdefiniowanie (określenie)zarówno problemu decyzyjnego jak i badawczego jest zdeterminowane

zrozumieniem przez badacza istniejącego stanu rzeczy. W związku z tym zaczyna on swoje postępowanie badawcze od:

1. Formułowania problemu decyzyjnego,

2. Analizy sytuacji,

3. Określenia hipotez badawczych,

4. Wywiadu z decydentem,

5. Zapoznania się z poprzednimi raportami.

3. Dobrane przy pomocy określonej metody jednostki próby mogą być poddane pomiarom pod warunkiem, że jednostki te zostały:

1. Wytypowane przez badacza,

2. Pobrane w terenie,

3. Dokładnie zaplanowane,

4. Operacyjnie zdefiniowane,

5. Rozdzielone pomiędzy osoby prowadzące pomiary.

4. Typem skali pomiarowej pozwalającej na stwierdzenie równości lub różności między mierzonymi cechami jest skala:

1. Absolutna,

2. Interwałowa,

3. Ilorazowa,

4. Porządkowa.

5. Jeżeli badacz chce ukryć rzeczywisty cel pomiaru przed respondentem to powinien on zastosować pytania:

1. Otwarte,

2. Pośrednie,

3. Zamknięte,

4. Bezpośrednie,

5. Sugestywne.

6. Skala Stapela jest przykładem skalowania wymuszonego ponieważ:

1. Jest skalą zrównoważoną,

2. Jest skalą jedenastodniową

3. Nie ma przedziałów neutralnych,

4. Nie muszą być zastosowane antonimy,

5. Wystarczy zastosować jeden przymiotnik lub rzeczownik dla każdej skali składowej.

7. Symbol statystyczny konkretnego wyrobu (2454-411) zawarty w SWW (Systematyczny Wykaz Wyrobów) oznacza,

że produkt ten został wytworzony przez:

1. Przemysł spożywczy,

2. Ogrodnictwo,

3. Przemysł metali niezależnych,

4. Przemysł materiałów budowlanych,

5. Przemysł elektromaszynowy.

8. Kryterium podziału paneli na statystyczną i dynamiczną jest:

1. Temat badania,

2. Sposób pomiaru,

3. Skład uczestników panelu,

4. Ciągłość pomiaru w czasie,

5. Przedmiot pomiaru.

9. Która z niżej wymienionych form pomiaru bezpośredniego charakteryzuje się największym poziomem głębokości:

1. Wywiad osobisty,

2. Metody projekcyjne,

3. Wywiad grupowy,

4. Obserwacja naturalna,

5. Rejestracja skaningowa.

10. Następujący schemat eksperymentu A/EM/: P1*P2 jest eksperymentem:

1. Jednogrupowym z dwoma pomiarami,

2. Dwugrupowym z jednym pomiarem,

3. Jednogrupowym z jednym pomiarem,

4. Dwugrupowym z dwoma pomiarami,

5. Jednogrupowy z serią pomiarów.

11. Najłatwiejsze do zliczenia są dane uzyskane z odpowiedzi:

1. Niewyskalowanych,

2. Na pytania zamknięte,

3. Rozłącznych,

4. Wyskalowanych,

5. Nierozłącznych.

12. Obliczanie średniego (standardowego) błędu szacunku średniej arytmetycznej konieczne jest gdy:

1. Liczebność próby jest mniejsza nią 30,

2. Używa się pojedynczych wartości i pomiaru próby,

3. Szacowanym parametrem jest odchylenie standardowe,

4. Próba składa się z więcej niż 50 jednostek,

5. Badana populacja ma rozkład asymetryczny.

13. Jednym z podstawowych warunków zastosowań metod ekstrapolacyjnych w prognozowaniu jest możliwość:

1. Określenie sposobu kształtowania się danego zjawiska w przyszłości,

2. Zastosowanie ilościowych metod statystycznych lub ekonometrycznych,

3. Przewidzenia tendencji rozwoju danego zjawiska w przyszłości,

4. Eliminacji zmian sezonowych i losowych,

5. Powiązania przyczyn ze skutkami.

14. Jeżeli wyniki badania nie przyczyniają się do całkowitego rozwiązania określonego problemu lub decyzji to badanie określa się jako:

1. Źle zaprojektowane (niedostosowane),

2. Całkowicie lub częściowo nietrafne,

3. Niezaakceptowane przez decydentów,

4. Nieefektywne,

5. Całkowicie nieprzydatne.

15. Główne czasopismo teoretyczne traktujące o badaniach marketingowych w Stanach Zjednoczonych zatytułowane

jest „Journal of Marketing Research: wydawane jest kwartalnie przez:

1. AMA

2. ACM

3. ABF

4. CASRO

5. Że z wyżej wymienionych.

SERIA IV

1. Wiadomo, że proces badań marketingowych jest procesem cyklicznym. Takim samym procesem cyklicznym jest także:

1. Analiza rynku,

2. Analiza marketingowa,

3. Badania konkurencji,

4. Analiza produktu,

5. Dobór próby.

2. Wszystkie formy pomiaru wyodrębnia się zgodnie z kryterium drogi przepływu danych od ich źródła do badania.

Wszystkie ankiety zalicza się do pomiarów:

1. Pierwotnych sondażowych bezpośrednich,

2. Pierwotnych sondażowych eksperymentalnych,

3. Pierwotnych sondażowych pośrednich,

4. Wtórnych,

5. Wymienionych łącznie w punktach a i c.

3. Wraz z rosnącą wielkością próby i rosnącą ilością prób dobranych metodą losowania prostego:

1. Rozkład średnich z tych prób jest coraz bardziej zbliżony do rozkładu normalnego,

2. Rośnie standardowy błąd średniej z próby,

3. Średnia wszystkich prób zbliża się do średniej z populacji,

4. Prawdziwe jest zarówno twierdzenie a jak i c

5. Łatwiej jest obliczyć prawdopodobieństwo wylosowania próby.

4. Pomiar porządkowy nie daje informacji o wielkości kolejnych różnic między przedziałami. Przyczyną tego stanu rzeczy jest:

1. Nierównomierne uporządkowanie cech na skali,

2. Brak jednostki miary,

3. Brak możliwości odejmowania i dodawania odległości na skali porządkowej,

4. Jakościowy charakter mierzonych cech,

5. Żadne z wyżej wymienionych czynników.

5. Pytanie otwarte charakteryzuje się tym, że odpowiedź na nie jest odpowiedzią:

1. Szacjonalną,

2. Wyskalowaną,

3. Całkowicie swobodną,

4. Nie wyskalowaną,

5. Bezpośrednią.

6. Zastosowanie jednolitych skal intensywności (skal porządkowych) opisanych werbalnie za pomocą pięciu

kategorii jednakowych dla każdego badanego przypadku jest charakterystyczne dla skal:

1. Stapela,

2. Semantycznej,

3. Pozycyjnej,

4. Likerta,

5. Porównywania parami

7. Z której nomenklatury towarowej stosowanej w handlu międzynarodowym pochodzi numer statystyczny o symbolu 735.91?

1. JHTEE,

2. SWW,

3. NTES,

4. SITC,

5. NCGCT.

8. Która za niżej wymienionych form pomiaru pośredniego zapewnia respondentowi osobistą anonimowość?

1. Ankieta audytoryjna,

2. Ankieta bezpośrednia,

3. Ankieta pocztowa,

4. Ankieta prasowa,

5. Ankieta ogólna.

9. Decyzję o wyborze wywiadu prostego standaryzowanego podejmuje badacz wówczas, gdy:

1. Prowadzący wywiad i respondent rozumieją się wzajemnie co do celu pomiaru i rodzaju poszukiwanych danych,

2. Respondent jest zdolny do dostarczenia potrzebnych danych,

3. Respondent jest skłonny udzielić odpowiedz,

4. Wymienione wyżej czynniki są spełnione jednocześnie,

5. Kwestionariusz wywiadu jest standaryzowany (z wyskalowanymi odpowiedziami).

10. Eksperyment jednogrupowy z serią pomiarów ma największe zastosowanie do oceny wpływu:

1. Zmian ocen na wielkość sprzedaży,

2. Kampanii reklamowej na zmiany w udziale w danym..........,

3. Dotychczasowej wielkości sprzedaży na cenę,

4. Opinii uczestników panelu na strategię promocyjną...........,

5. Dotychczasowej tendencji w zakupach na politykę reklamową firmy.

11. Najbardziej poprawna logicznie i najłatwiejsza do interpretacji jest tabulacja dwudzielna obejmująca dane pochodzące

1. Tylko z odpowiedzi rozłącznych,

2. Z odpowiedzi wyskalowanych,

3. Z odpowiedzi nierozłącznych i rozłącznych jednocześnie,

4. Tylko z odpowiedzi nierozłącznych,

5. Z odpowiedzi na pytania zamknięte.

12. Średnia liczba pracowników zatrudnionych w firmach ......(w tym polonijnych) w Polsce w roku 1986 oszacowana

na podstawie pomiaru .........elementowej próby, z której średni .......-300 pracowników, a odchylenie standardowe

s......przy poziomie ufności 93,445, dla którego.....wyniosła:

1. 260-340

2. 270-330

3. 290-320

4. 290-310

5. 295-305

13. Pary współrzędnych (t1,y1), (t2,y2),.....(tn,yn) w układzie równań w metodzie najmniejszych kwadratów określają:

1. parametry linii prostej,

2. współczynnik kierunkowy prostej,

3. poszczególne pomiary,

4. trend rozwojowy prognozowanego zjawiska,

5. zupełnie co innego.

14. W najpełniejszy sposób badacz bierze udział w zastosowaniu wyników badania w praktyce, gdy występuje w roli:

1. Doradcy,

2. Prezentera wyników badania,

3. Obserwatora,

4. Członka kadry kierowniczej,

5. Niezależnego badacza.

15. Badanie ankietowe przeprowadzone w Wielkiej Brytanii w 1984 roku wykazało, że procent przedsiębiorstw

prowadzących badania we własnym zakresie lub zlecając je agencjom badawczym wynosi:

1. 27, b) 45, c) 62, d) 81, e) 93.

SERIA V

1. klasyfikację badań marketingowych przeprowadza się według różnych kryteriów. Najbardziej rozbudowana jest

klasyfikacja według zasady:

1. przedmiotu badania,

2. horyzontu czasowego,

3. podmiotu badania,

4. szczegółowości badania,

5. ciągłości badania.

2. Plan badania opinii klientów sklepów wolnocłowych „Baltony” został opracowany przy zastosowaniu:

1. Wywiadu osobistego,

2. Metody CPM,

3. Elektronicznej techniki obliczeniowej,

4. Metody MCX,

5. Metody PERT.

3. Wzrost liczebności próby polepsz pozycję estymatora, ale wielkość próby:

1. Nie zależy od wielkości populacji,

2. Decyduje o kosztach badania,

3. Zależy od liczebności populacji badanej,

4. Jest uzależniona od rodzaju estymatora,

5. Jest ograniczona od góry.

4. Budowa skali jednobiegunowej polega na tym, że przy danym jednym biegunie drugi biegun jest jego:

1. Negacją, b) Zaprzeczeniem, c) Odbiciem, d) Przeciwieństwem, e) Odwzorowaniem.

5. Pytanie zamknięte charakteryzuje się tym, że odpowiedź na nie jest odpowiedzią:

1. Pośrednią,

2. Niewyskalowaną,

3. Ograniczoną,

4. Bezpośrednią,

5. Wyskalowaną.

6. Pomiar wieloczynnikowy ma największe zastosowanie do:

1. Testowania nowego produktu,

2. Porównywania kilku produktów w jednym układzie współrzędnych,

3. Testowania kilku nowych produktów,

4. Testowania kilku środków reklamy jednocześnie,

5. Oceny preferencji nabywców względem dwóch produktów.

7. Przedmiotem pomiaru wtórnego są:

1. Źródła pisane,

2. Cechy osób, rzeczy i zdarzeń,

3. Źródła drukowane,

4. Źródła pierwotne i wtórne,

5. Wyniki wcześniejszych pomiarów pierwotnych lub wtórnych.

8. Która z wymienionych niżej form pomiaru pośredniego zapewnia ankieterowi największą kontrolę?

1. Ankieta komputerowa,

2. Ankieta pocztowa,

3. Ankieta audytoryjna,

4. Ankieta bezpośrednia,

5. Ankieta opakowaniowa.

9. Testy obrazkowe są instrumentami pomiarowymi w ramach metod:

1. Konstrukcji,

2. Uzupełnień,

3. Skojarzeń,

4. Wyobrażeń,

5. Zarówno konstrukcji jak i wyobrażeń.

10. Podstawowym zadaniem grupy kontrolnej w eksperymencie jest:

1. Eliminacja wszystkich błędów,

2. Wyodrębnienie i określenie niektórych źródeł błędów,

3. Kontrolowanie przebiegu eksperymentu,

4. Umożliwienie losowego doboru jednostek w grupie eksperymentalnej,

5. Pomiar ubocznych efektów oddziaływania zmiany eksperymentalnej.

11. O poprawności logicznej każdej klasyfikacji decyduje przede wszystkim:

1. Zasada zupełności,

2. Zasada dokładności,

3. Zasada rozłączności,

4. Zasada zupełności i rozłączności jednocześnie,

5. Zasada jednoznaczności.

12. Standardowy błąd proporcji dla p=0,50 szacowanej z próby n=26 wynosi:

1. 0.05 b) 0,10 c) 0,15 d) 0,20 e) 0,25

13. metoda średnich ruchomych (absolutna) jest stosowana do celów prognozowania wówczas gdy zebrane dane

charakteryzuje trend liniowy a wahania sezonowe są:

1. addytywne,

2. cykliczne,

3. o stałej amplitudzie,

4. multiplikatywne,

5. addytywne i o stałej amplitudzie.

14. Ochroną prawną w zakresie badań marketingowych objęto:

1. Tylko respondentów,

2. Tylko klientów,

3. Klientów, respondentów i firmy badawcze,

4. Tylko firmy badawcze,

5. Nikogo spośród wyżej wymienionych.

15. Największą firmą badawczą w Wielkiej Brytanii jest:

1. Research Burean,

2. A.C.Nielsen,

3. Top Group,

4. AGB

5. MRB International.

SERIA X

1. Do jakiego kryterium badań zalicza się badania konkurencji wg kryterium przedmiotowego:

1. Polityki sprzedaże eksportowej,

2. Procesów innowacyjnych,

3. Skuteczności badań marketingowych,

4. Otoczenia krajowego i zagranicznego,

5. Nabywców i ich wymagań.

2. Do jakiego rodzaju błędów zalicza się różnicę między danymi niezbędnymi do rozwiązania określonego

problemu decyzyjnego a danymi poszukiwanymi przez badacza:

1. Pomiaru,

2. Analizy danych,

3. Problemu badawczego,

4. Niewłaściwego stosowania próby,

5. Braku analizy sytuacji.

3. Jednostka próby może być jednocześnie elementem populacji badanej. Element populacji jest zwykle jednostką naturalną na przykład:

1. Plan nowego obszaru,

2. Rodzina,

3. Mieszkańcy domu,

4. Pracownicy przedsiębiorstwa,

5. Produkt.

4. Która z podanych niżej skróconych definicji popytu jest najbardziej zbliżona do operacyjnej definicji popytu?

1. Popyt jako ilość towaru,

2. Popyt jako zapotrzebowanie,

3. Popyt jako zamiar kupna,

4. Popyt jako ......... przeznaczonego na zakupy,

5. Popyt jako potrzeba.

5. W ramach stosowanej metody odpowiedzi losowych zadano respondentowi dwa pytania:

A-„Czy dokonał pan kradzieży w tym sklepie w ostatnim miesiącu?”

B-„Czy urodził się pan w maju?”

Zakładając, że mechanizm losowania jakim jest rzut monetą daje równe szanse wyboru pytania

A i B, proporcja twierdzącej odpowiedzi na dwa pytania (A i B) łącznie wyniosła 0,10 a ze statystyk spisu powszechnego wynika,

że 10% mieszkańców urodziło się w maju - proporcja twierdzącej odpowiedzi na pytanie A wyniosła:

a) 5%, b) 6%, c) 7%, d) 8%, e) 10%.

6. Która skala jest głównym elementem skali pozycyjnej?

1. Jednostkowa, b) Nominalna, c) Porządkowa, d) Rang, e) Ocen.

7. Która z niżej wymienionych ksiąg adresowych jest wydawana w Polsce przez GUS?

1. REGON,

2. Leksykon Eksporterów,

3. Panorama Firm,

4. BKF,

5. Żadna z wyżej wymienionych.

8. Co zalicza się do głównych zalet ankiety pocztowej:

1. Indywidualność każdego przypadku,

2. Możliwość zastosowania procedury zmniejszania BBO (błąd braku odp)

3. Możliwość doboru reprezentatywnej próby losowej,

4. To co się mieści w punktach a i c jednocześnie,

5. Bezpośredni kontakt z respondentem.

9. Jakim skrótem oznaczono w Europie system zunikowanego kodu produktu za przykładem amerykańskim w celu

rejestracji skaningowej ruchu towarów w sieci detalicznej:

1. IANA, b) UPC, c) EUR, d) ANA, e) EAN.

10. Jakimi wymiarami charakteryzuje się eksperyment w postaci modelu czynnikowego:

1. 4*4, b) 2*3, c) 3*4, d) 3*3, e) wszystkimi wymienionymi.

11. Jakim skrótem określa się system skomputeryzowanych wywiadów osobistych:

1. CAWI, b) SWOT, c) CATI, d) FOSDIC, e) CAPI.

12. W roku 1995 sprzedano towarów za 50 mln zł, a w roku 1999 - za 95 mln zł. Ile wyniosło średnioroczne tempo wzrostu sprzedaży tych towarów w latach 1995-1999?

1. 21%, b) 20%, c) 18%, d) 15%, e) 17%.

13. Odmianą jakiej metody jest metoda analogii historycznej jako jakościowej metody prognozowania:

1. Scenariusza, b) przypadków, c) delfickiej, d) opinii specjalistów, e) ekstrapolacji.

14. Kiesy stosuje się wykresy liniowe:

1. Gdy dane odzwierciedlają długi okres rozwoju zjawiska,

2. Kilka zjawisk porównuje się na tym samym wykresie,

3. Zależy nam na dynamicznym ukazaniu danego problemu,

4. Gdy wykres zawiera prognozę lub szacunek,

5. Gdy wystąpi jakakolwiek wymieniona wyżej sytuacja.

15. Która z wymienionych firm amerykańskich ma największe dochody spoza granic USA:

1. IMS International, b) Burke, c) Luis Harris, d) Arbirron, e) A.C. Nielsen.

SERIA XI

1. W Europie pierwszym czasopismem na temat badań rynkowych wydawanym od 1958 roku było:

1. Marketing Research,

2. Marketing and Research Today,

3. Journal of Business Research,

4. Journal of the Market Research Society,

5. Journal of Consumer Research.

2. Do której z niżej wymienionych grup metod zbierania danych należy ankieta interwałowa:

1. Sondaży bezpośrednich,

2. Metod eksperymentalnych,

3. Pomiarów wtórnych przy pomocy internetu,

4. Sondaży pośrednich,

5. Do żadnej z wyżej wymienionych.

3. Jak nazywają się składowe ilości jednostek próby z obliczonej wcześniej wielkości próby podzielone proporcjonalnie do udziałów poszczególnych warstw w badanej populacji:

1. Jednostkami typowymi,

2. Kwotami,

3. Jednostkami naturalnymi,

4. Grupami wielodzielnymi,

5. Grupami zależnymi od siebie.

4. Jak nazywa się definicja zawierająca zalecenia służące pomiarowi definiowanej cechy:

1. Teoretyczna,

2. Pomiarowa,

3. Koncepcyjna,

4. Instrumentalna,

5. Operacyjna.

5. Czym charakteryzują się pytania, które wszyscy respondenci rozumieją i interpretują jednakowo:

1. Sugestywnością,

2. Tendencyjnością,

3. Bezpośredniością,

4. Otwartością,

5. Jednoznacznością.

6. Jak nazywa się pomiar dotyczący wielu powiązanych ze sobą cech jednego produktu preferencji respondentów:

1. Skalowaniem wielowymiarowym,

2. Pomiarem wieloczynnikowym,

3. Pomiarem preferencji,

4. Pomiarem pełnego profilu wyboru,

5. Pomiarem semantycznym.

7. Do której nomenklatury towarowej należy kod statystyczny o symbolu 1053-122:

1. SWW, b) STC, c) NC, d) NCGTC, e) BTN.

8. W której z niżej wymienionych ankiet ankieter bierze bezpośredni udział:

1. Audytoryjna, b) Telefoniczna, c) Pocztowa, d) Prasowa, e) Ogólna.

9. Do jakich pomiarów używa się tachistoskopu oraz wideokamery sprzężonej z komputerem:

1. Pomiarów projekcyjnych,

2. Pomiarów psychograficznych,

3. Pomiarów fizjologicznych,

4. Pomiarów prawdomówności,

5. W żadnej z wyżej wymienionych.

10. Który z niżej wymienionych modeli eksperymentów zastosowałbyś w celu zidentyfikowania wpływu zmiennej eksperymentalnej na tendencję w sprzedaży:

1. Dwugrupowy z serią pomiarów,

2. Eksperyment Salomona,

3. Dwugrupowy w dwoma pomiarami,

4. Dwugrupowy z czterema pomiarami,

5. Symulowany.

11. Jakim symbolem oznacz się skomputeryzowane wywiady osobiste:

1. CAM, b) FOSDIC, c) CAPI, d) MRT, e) SPSS.

12. Który z niżej wymienionych testów służy do weryfikacji wyników z pomiaru porządkowego:

1. Chi - kwadrat,

2. Test ANOVA pojedynczy,

3. Test Z,

4. Test wielomianowy,

5. Test K - S.

13. Jak nazywa się ranking oceny metod zbierania danych ze względu na etykę związaną z tym postępowaniem:

1. System Zipfa,

2. System Wade'a,

3. Ranking Davisa,

4. Ranking Crawforda,

5. Kodeks etyczny.

14. Kto jest właścicielem największej na świecie firmy badawczej:

1. WPP Group Plc,

2. Control Data,

3. Daz & Bradstreet,

4. Saatchi & Saatchi,

5. Booz Allen & Harnilton.

15. Jak nazywa się badanie polegające na regularnym zbieraniu danych, analizie i udostępnieniu ich zainteresowanym klientom:

1. Syndicated Research,

2. Standardowe,

3. Prasowe,

4. Syndykatowe,

5. Full - service.

SERIA XII

1. Przez kogo został założony pierwszy dział marketingowy w roku 1911 w firmie The Curtis Publishing Company:

1. Nicholasa - Sheparda, b) Parlina, c) Fredericka, d) Nielsena, e) Duncana.

2. W przypadku planowania bardzo skomplikowanych i długotrwałych badań marketingowych stosować można metody planowania sieciowego. Która z tych metod pozwala na jednoczesne planowanie określenia kosztów badania:

1. PERT, b) SPSS, c) MRT, d) Metoda diagramu, e) żadna z wyżej wymienionych.

3. Która z niżej wymienionych skal pomiarowych ma umowny punkt zerowy:

1. Proporcjonalna,

2. Jednostkowa,

3. Absolutna,

4. Nominalna,

5. Porządkowa.

4. Który rodzaj pytań pozwala na ograniczenie błędu związanego ze zdolnością respondenta do odpowiedzi:

1. Pytania zamknięte,

2. Pytania sugestywne,

3. Pytania filtrujące,

4. Pytania otwarte,

5. Pytania bezpośrednie.

5. Jak nazywa się złożona skala postaw składająca się z kilku lub kilkunastu siedmiostopniowych skal porządkowych,

z których każda jest na biegunach antonimami:

1. Skala semantyczna,

2. Skala Stapela,

3. Skala rang,

4. Skala pozycyjna,

5. Skala Likerta.

6. Do jakiego rodzaju źródeł informacji zaliczamy opakowania produktów konkurencyjnych:

1. Zewnętrznych źródeł pierwotnych,

2. Zewnętrznych źródeł wtórnych,

3. Wewnętrznych źródeł wtórnych,

4. Baz danych konkurencji,

5. Do żadnych z wyżej wymienionych.

7. W której z niżej wymienionych pośrednich metod zbierania danych może mieć zastosowanie w pełni reprezentatywna próba losowa:

1. Ankieta prasowa,

2. Ankieta audytoryjna,

3. Ankieta faksowa,

4. Ankieta pocztowa,

5. Ankieta internetowa.

8. Z badań prowadzonych systematycznie przez firmę Walker Research w USA wynika, że preferencje wyboru metody

zbierania danych w badaniach marketingowych różnią się między badaczami a respondentami.

W stosunku do której metody zbierania danych preferencje te różnią się najbardziej:

1. Wywiad telefoniczny,

2. Wywiad osobisty,

3. Wywiad grupowy,

4. Obserwacja,

5. Wywiad grupowy,

6. Ankieta pocztowa.

9. Do której grupy eksperymentów zalicza się eksperyment w postaci modelu czynnikowego:

1. Losowych,

2. Z serią pomiarów,

3. Rzeczywistych,

4. Statystycznych,

5. Quasi - eksperymentów.

10. Jaką literą oznacza się największą różnicę między wartościami skumulowanego rozkładu empirycznego i

wartościami skumulowanego rozkładu hipotetycznego w teście K - S:

1. Wartość U, b) Wartość H, c) Wartość X, d) Wartość Y, e) Wartość D.

11. Do której grupy metod prognozowania zalicza się metody wczesnych symptomów:

1. Ekstrapolacyjnych,

2. Przyczynowo - skutkowych,

3. Jakościowych,

4. Regresji,

5. Do żadnej z wyżej wymienionych.

12. Jaką metodę graficzną należy zastosować w raporcie gdy dane odzwierciedlają kilka zjawisk jednocześnie ,

długi okres ich rozwoju oraz gdy chcemy porównać je między sobą:

1. Histogram, b) Wykres kołowy, c) Wykres liniowy, d) Piktogram, e) Wykres słupkowy.

13. Jakiemu problemowi przeciwstawiane jest prawo do poszukiwania obiektywnej prawdy w zakresie etyki badań marketingowych:

1. Anonimowości danych,

2. Poufności danych,

3. Wymuszonej zgody respondenta,

4. Ochrony respondentów,

5. Niewymuszonej zgody respondenta.

14. Kto jest właścicielem największych na świecie firm badawczych A. C. Nielsen oraz IMS International Inc. mających swoje

siedziby w USA:

1. Control Data,

2. WPP Group Plc.

3. Dun & Bradstreet,

4. KLP Group Plc.

5. Saatchi & Saatchi.

15. Która z niżej wymienionych polskich firm badawczych ma swoją siedzibę w Gdańsku:

1. Pracownia Badań Społecznych,

2. Demoskop,

3. Eurotest,

4. ProMedia,

5. Estymator.

SERIA VI

1. Największa organizacja na świecie zrzeszająca członków badaczy indywidualnych: MRS

2. Największe czasopismo w Europie: JMRS Journal of Marketing

Research Society

3. W skali nominalnej zmienne z jednej lub dwóch prób niezależnych szacowana jest za pomocą testu: χ2

4. Wczesnymi symptomami wzrostu popytu w gospodarce jest: zwiększona liczba kupowanych dóbr

konsumpcyjnych

5. Co jest jednocześnie źródłem pierwotnym i wtórnym: folder

6. W skali przedziałowej mapy przyjęte są jako: arbitralne

7. Jaka skala jest stosowana do pomiaru preferencji: skala semantyczna

8. O czym decyduje wybrana metoda doboru próby: o reprezentatywności

9. Do jakiego rodzaju instrumentów pomiarowych zalicza się skaner: do konwencjonalnych

10. Co musi uzyskać badacz od uczestników wywiadu grupowego, aby badanie mogło być przeprowadzone:

Niewymuszoną zgodę

SERIA VII

1. Internatonal Trade Forum wydaje: UNCTAD - GATI

2. Marketing Sales Management wydaje: indeks siły nabywczej

3. Trafność daje błędy systematyczne

4. Przed rozpoczęciem pomiaru wybiera się metodę analizy danych. Użyteczną metodą umożliwiającą dobór sposobów analizy jest: pomiar imitacyjny z użyciem

wstępnie zaprojektowanych instrumentów

5. Jaki program komputerowy ma mój oddział (firma badawcza) w Krakowie: SPSS

1. Jaki procent kobiet odpowiedział na pytanie „Czy przerywała pani ciążę?” tak 32%

2. Za pomocą jakiej metody zostało przeprowadzone badanie sklepu Baltona w 1984r metoda PERT

3. Jaka organizacja wydała IMR AMA

4. Kto tworzył definicję badań marketingowych:

”Funkcją badań marketingowych jest dostarczanie informacji w celu wsparcia kierownictwa przedsiębiorstw w podejmowaniu trafnych decyzji” D. I. Hawkins i D. S. Tull

„Systematyczne projektowanie, zbieranie, analizowanie i prezentowanie danych i wyników badań związanych istotnie ze specyficzną sytuacją marketingową „ P. Kotler

„Badania marketingowe wiążą daną organizację z jej rynkowym otoczeniem. Organizacja projektuje badania, gromadzi, analizuje i interpretuje dane, aby pomóc kierownictwu w zrozumieniu otoczenia, zidentyfikowaniuproblemów i sprzyjających sytuacji oraz w rozwoju i przeprowadzaniu działań na określonych rynkach” D. Aaker i G. Day

5. Ile wynosi kombinacja możliwości wyboru metod losowych i nielosowych doboru i prób: 2*16=32

6. Za pomocą jakich środków prezentuje się użytkownikom wyniki badania zawierającego instrukcję definiującą użyte instrumenty: konspekt

7. Jak nazywają się usługi polegające na regularnym zbieraniu danych na określony temat: Syndicated research

8. Która z metod szacowania BBO jest najbardziej efektywna: metoda próbki z próby

9. Jaką gałąź gospodarki oznacza kod 2809 - ITMZ: przemysł spożywczy

10. Co oznaczają liczby w kodzie kreskowym 73100400113186: numer produktu

11. Czynności odwzorowania mierzonej cechy za pomocą wybranej skali nazywa się skalowaniem

12. Polega na przyporządkowaniu określonych symboli cechom mierzonych obiektów: pomiar

13. Jakie pytania należy zadawać aby ukryć cel pomiaru przed respondentem: pytania pośrednie, neutralne

14. Co to jest dobór próby: jest to sposób w jaki elementy

Populacji badanej są wybierane z tej populacji

15. Jaki jest pierwszy etap realizacji projektu: Jest to zbieranie danych ze źródeł

wtórnych, pozostała część danych pochodzi ze źródeł pierwotnych

16. Co się dzieje, gdy badanie nie daje oczekiwanego rezultatu: jest źle sformułowana ankieta

17. Co wpływa na zmianę wyników badania:

18. Instrumenty konwencjonalne: kwestionariusz, test, dziennik,

instrukcja, model

19. Kiedy oblicza się średni błąd próby: gdy n>30

20. Co to jest pomiar: przyporządkowanie określonych

symboli cechom mierzonych obiektów

21. Kiedy się stosuje skale nominalne:

22. Jakie pytania zawarte w kwestionariuszu najlepiej się sumuje: zamknięte i wyskalowane

23. Jak wygląda skala semantyczna: zestaw kilku lub kilkunastu skal

porządkowych

1. Nomenklatura ITHZ: przemysł spożywczy

2. Co to jest, gdy problem porównywalności dostępnych danych występuje wówczas, gdy badacz ma do czynienia z wywiadem bezpośrednim, różnymi klasyfikacjami towarów w statystykach międzynarodowych oraz w statystykach handlu zagranicznego poszczególnych krajów: klasyfikacja towarów

3. Podział paneli ze względu na skład uczestników: statyczne i dynamiczne

27. Co to jest kodowanie: przyporządkowanie symboli danym zawartym

w instrumentach pomiarowych

28. Czym różnią się od siebie średnia arytmetyczna, mediana i dominanta:

29. W przewidywaniu czego niewielkie możliwości mają metody ekstrapolacyjne: punktów zwrotnych w których tempo wzrostu

lub spadku gwałtownie się zmienia

30. W jakiej grupie firm są najbardziej popularne badania marketingowe: firmy wydawnicze i rozpowszechniające infor

31. Największa firma badawcza w Wielkiej Brytanii:

32. Wzór na średni błąd próby:

33. Wzór Likerta:

34. Czego początkiem była służba informacyjna banków: gazet

35. Które ze skal pozwalają na stwierdzenie równości lub różnic między mierzonymi cechami: skale nominalne

36. Czego przykładem jest skala Stapela: skalowania wymuszającego bo nie ma

przedziałów neutralnych

37. Jeżeli każdej pozycji towarowej przyporządkowany jest symbol cyfrowy z zakodowaną klasyfikacją to mówi się o:

Jedności nomenklatury i klasyfikacji

38. Jakie odpowiedzi najłatwiej się zlicza: wyskalowane

39. SNTZM - Scalona Nomenklatura Handlu Zagranicznego

CN - Scalona Nomenklatura Towarów Krajów Wspólnoty Europejskiej

SWW - Systematyczny Wykaz Wyrobów

STTC - Scalona Klasyfikacja Handlu Międzynarodowego

PIHZ - Polska Izba Handlu Zagranicznego

KIG - Krajowa Izba Gospodarki

40. Odpowiedzi na pytania zamknięte są: wyskalowane

41. Która metoda ankiety daje największą kontrolę: ankieta bezpośrednia

42. Jaki jest wpływ grupy kontrolnej w eksperymencie:

43. Do jakich metod należą testy obrazkowe: metod konstrukcji

44. Co jest przedmiotem pomiaru wtórnego: nie jest osoba, rzecz, stan czy zdarzenie

lecz cechy wymienionych kategorii

45. O poprawności logicznej w klasyfikacji świadczy:

46. Najobszerniejszym kryterium przy klasyfikacji rodzajów badań marketingowych jest: kryterium przedmiotowe

47. Do czego służy pomiar wieloczynnikowy: to pomiar preferencji respondentów

względem kilku powiązanych ze sobą czynników (cech) jego produktów. Ma on zastosowanie głównie do testowania nowych produktów i środków reklamy.

48. Do czego służy średnia ruchoma: do programowania trendu liniowego o wahaniu..

49. Kto ma ochronę prawną: respondenci, klienci,grupy społ.,firmy badawcze

50. Na jakiej ulicy mieści się w Warszawie GUS: Aleja Niepodległości

51. Jakie metody są najbardziej pogłębione: metody projektowe

52. Która z metod jest najgłębsza: ankieta osobista lub wywiad grupowy

53. Kiedy stosujemy metodę ekstrapolacji: istotą tej metody jest ilościowe przedłużenie

Dotychczasowych tendencji na pewien okres w przyszłości. Metody te są efektywne w prognozowaniu krótkookresowym.

54. W ramach definiowania problemu badawczego najważniejszą wstępna czynnością badacza jest ścisłe określenie:

Problemu decyzyjnego

55. W praktyce istnieje pewna maksymalna ilość metod doboru losowego i nielosowego prób. Ta liczba to: 32

56. Jednoznaczność oznacza, że: wszyscy respondenci rozumieją pytania jednako

57. Wynikiem analizy danych zebranych przy pomocy skali semantycznej jest zwykle obraz graficzny. Zestaw linii nazywa się:

Profilem polaryzacji

58. Problem porównywalności dostępnych danych występuje w statystykach międzynarodowych wówczas, gdy mamy do czynienia z różnymi: klasyfikacjami towarowymi

59. Jeżeli po upływie pewnego czasu część respondentów odmawia udziału w eksperymencie lub następują inne nieprzewidziane zmiany naturalne, to mówimy, że błąd spowodowany został: zmianą składu grupy

60. Poza konkretnymi metodami dokonywania poprawek i uzupełnień należy przestrzegać pewnych zasad ogólnych poprzez:

Stosowanie wszystkich podanych pomiarów jednocześnie

61. Metody ekstrapolacyjne wykazują niewielkie możliwości w przewidywaniu: punktów zwrotnych, w których tempo wzrostu

Lub spadku gwałtownie się zmienia

62. Wzory i kopie użytych w badaniu instrumentów pomiarowych (konwencjonalnych) najlepiej jest zaprezentować słuchaczom z wykorzystaniem: konspektu

63. Co jest jednocześnie źródłem pierwotnym i wtórnym: folder

64. W skali przedziałowej miary przyjęte są jako: arbitralne

65. Jaka skala stosowana jest do pomiaru preferencji: skala semantyczna

66. O czym decyduje wybrana metoda doboru próby: o reprezentatywności

67. Do jakiego rodzaju instrumentów pomiarowych zalicza się skaner: konwencjonalne

68. Kwestionariusz testowany jest najczęściej za pomocą: wywiadu osobistego lub telefonicznego

69. International Trade Forum wydaje: UNCTAD - GATI

70. Marketing Sales Management wydaje: indeks siły nabywczej

71. Trafność daje: błędy statystyczne

72. Tachistoskop służy do pomiaru: ruchu gałek ocznych

73. Najlepszy poziom kontroli jest w ankiecie: audytoryjnej

74. Manipulowanie modelami eksperymentalnymi w celu uzyskania informacji to: symulacja

75. Która z wymienionych firm badawczych ma swoją siedzibę w Gdańsku: Eurotest

76. Jaka firma nie należy do zrzeszenia CASRO: Gallup

77. Czego dotyczy krzywa poligraficzna: pomiary fizjologiczne

78. Skomputeryzowane badanie telefoniczne wywiadów to: CATI

79. Czego nie obejmuje pomiar kwotowy: metod statystycznych

80. Która metoda jest najbardziej pogłębiona: wywiad grupowy

81. Które z badań wychodzi od decydenta: sporadyczne

82. Jak przejść od problemu decyzyjnego do badawczego:

83. Który z modeli zastosowałbyś w celu identyfikacji wpływu zmiennej eksperymentalnej na tendencję spadku:

Model dwugrupowy z serią pomiarów

84. Czego dotyczy ekstrapolacja:

85. Instytucja w USA zrzeszająca tylko firmy badawcze to: CASRO

86. Kto wydaje Industry Image Study: Walker Research

87. Kto napisał pierwszą książkę o badaniach marketingowych: Duncan

88. Badanie, w którym poddaje się pomiarowi wszystkie składniki próby to: badanie wyczerpujące

89. Kto prowadzi wywiad grupowy: moderator

90. Jaka metoda losowania jest najbardziej adekwatna do doboru dużych prób z dużych wyborów:

Losowanie systematyczne

91. Metody wątpliwe etycznie to: bezpośrednie obserwacje z ukrycia lub w tajemnicy

92. Która z firm w Polsce była największa w 1999r: GFK

93. Która z metod BBO zakłada, że im grupa jest mniej chętna na udzielenie odpowiedzi tym większego błędu należy oczekiwać:

Ekstrapolacji

94. Co zostało uznane za najbardziej nieetyczne w stosunku do badań Akaah: lustro weneckie

95. Która ze skal może wyrażać temperatury i daty: przedziałowa

96. Które pytanie daje respondentowi możliwość odpowiedzi: otwarte

97. Podstawowym kryterium podziału metod postępowania w badaniach marketingowych jest: zakres

98. Z czego korzysta przedsiębiorstwo by uzyskać dane o udziale klientów, produktów: zew. źródła wtórne

99. Do jakiej grupy zalicza się metodę wejścia - wyjścia: przyczynowo - skutkowa

100. W którym roku Europa prześcignęła USA w wydatkach na badania marketingowe: 1987

101. Która firma badawcza miała największe obroty w Polsce w 1999r: SMG/KRC

102. Jaki wykres przedstawia rozkłady jakiegoś zjawiska i w sumie daje 100%: kołowy

103. Przy której ankiecie ankieter ma bezpośredni udział: audytoryjna

104. Jaki rodzaj błędów powstaje w wyniku zbierania złych danych: błąd problemu badawczego

105. Jak nazywa się najdroższe kompleksowe zabezpieczenie: audyt bezpieczeństwa

106. Do jakiej grupy skal zaliczamy skalę semantyczną: porządkowych

107. Jak w Internecie nazywa się coś co ma bazy danych: wyszukiwarka

108. Jaki test stosujemy dla pomiarów porządkowych z wieloma zmiennymi: K - S lub ANOVA

109. Jaka technika wykorzystuje wycinki z gazet: kolażowa

110. Ile liczb może mieć nazwa zmiennej w programie SPSS: 60

111. Jak nazywa się pytanie pomocnicze związane ze zdolnością respondenta do odpowiedzi: filtrujące

112. Da jakiego rodzaju badań zaliczamy gdy dyrektor ds. marketingu otrzymuje informacje o elastyczności popytu, o wielkości kosztów działalności marketingowych:

a) sporadyczne, b) ciągłe, c) opisowe

113. Które z pytań zaliczyłbyś do problemu decyzyjnego:

a) gdzie należy wybudować sklep, b) W jakiej miejscowości jest nasza konkurencja, c) Jakie koszty ponosi konkurencja.

114. Jaka nieamerykańska firma w 1998r. Przeprowadziła najwięcej badań: GTR group

115. Jaką nazwę nosi nowa wyszukiwarka wynaleziona przez IBM:

a) Clever b) HotBot c) Mami d) Intsee

116. Kto nadaje numer czterocyfrowy z trzynastocyfrowego kodu klasyfikacji produktu: CKK

117. Przy pomocy jakiego testu dokonujemy weryfikacji pomiaru porządkowego: K - S

118. W roku kalendarzowym wartość zero jest wartością: umowną

119. Gdy zatrudniamy pracowników konkurencji to z jaką sytuacją mamy do czynienia: wątpliwie moralną

120. Jak nazywa się złożona skala składająca się z kilkunastu siedmiostopnoiwych skal: semantyczna

121. Największa firma badawcza w Polsce z poza Warszawy w 1999r. To: Pracownia Badań społecznych

SERIA 2

1. Dane o rynkach zbierano już w średniowiecznej Europie, czego dowodem było m.in. : to, że każdy z domów bankowych dysponował własną służbą informacyjną. Działalność tych służb dała początek : b) Pierwszym gazetom.

2. W ramach definiowania problemu badawczego najważniejszą wstępną czynnością badacza jest ścisłe określenie:

3. W praktyce istnieje pewna maksymalna ilość metod doboru losowego i nielosowego prób. Ta maksymalna liczba metod wynosi : c) 32 .

4. Czynność odwzorowania mierzonej cechy przy pomocy wybranej skali nazywa się: d) Skalowaniem.

5. Układając pytania kwestionariuszowe należy dążyć do ich jednoznaczności. Jednoznaczność oznacza, że: d) Wszyscy respondenci rozumieją pytanie jednakowo.

6. Wynikiem analizy danych zebranych przy pomocy skali semantycznej jest zwykle obraz graficzny przedstawiający porównawczy zestaw linii nazywany: c) profilem polaryzacji.

7. Problem porównywalności dostępnych danych występuje w statystykach międzynarodowych wówczas gdy mamy do czynienia z różnymi: b) klasyfikacjami towarowymi.

8. Za najbardziej efektywną metodę oszacowania błędu wynikającego z braku odpowiedzi (BWBO) uważa się: b) metodę próbki z próby.

9. Oto przykład trzynastopozycyjnego kodu kreskowego EAX : 7 3 10040 013186. W podkreślonych linią ciągłą 5 cyfrach zakodowano: b) numer produktu.

10. Jeżeli po upływie pewnego czasu część respondentów odmawia udziału w eksperymencie lub następują inne nieprzewidziane zmiany naturalne, to mówimy, że błąd spowodowany został: a) zmianą składu prób.

11. Poza konkretnymi metodami dokonywania poprawek i uzupełnień należy przestrzegać pewnych zasad ogólnych poprzez: e) Stosowanie wszystkich podanych sposobów jednocześnie.

12. Średnia arytmetyczna, mediana i dominanta różnią się między sobą w przypadku: b) Asymetrycznego rozkładu częstości wyników pomiarów .

13. Metody ekstrapolacyjne wykazują niewielkie możliwości w przewidywaniu: c) punktów zwrotnych, w których tempo wzrostu lub spadku gwałtownie się zmienia.

14. Wzory i kopie użytych w badaniu instrumentów pomiarowych (konwencjonalnych) najlepiej jest zaprezentować słuchaczom z wykorzystaniem: b) handoutu (KONSPEKT) .

15. Usługi badawcze polegające na zbieraniu regularnie danych na określony temat, przetwarzanie ich i sprzedawanie zainteresowanym klientom w formie raportów lub okresowych opracowań, zwykle na zasadzie subskrybcji (nie zlecenia) nazywane są w Stanach Zjednoczonych i Wielkiej Brytanii usługami typu: b) Syndicated research (services).

SERAI 3

1. Jedna z definicji mówi, że „funkcją badań marketingowych” jest dostarczanie informacji, która mogłaby wesprzeć przedsiębiorstwo w podejmowaniu decyzji. Autorami tej definicji są: d) Tull i Hawkins.

2. Trafne zdefiniowanie ( określenie ) zarówno problemu decyzyjnego jak i badawczego jest zdeterminowane zrozumieniem przez badacza istniejącego stanu rzeczy. W związku z tym zaczyna on swoje postępowanie badawcze od: b) analizy sytuacji.

3. Dobrane przy pomocy określonej metody jednostki próby mogą być poddane pomiarom pod warunkiem, że jednostki te zostały: c) operacyjnie zdefiniowane.

4. Typem skali pomiarowej pozwalającej na stwierdzeniu równości lub różności między mierzonymi cechami jest skala: c) nominalna.

5. Jeżeli badacz chce ukryć rzeczywisty cel pomiaru przed respondentem to powinien on zastosować pytania : b) pośrednie.

6. Skala Stapela jest przykładem skalowania wymuszającego ponieważ: c) nie ma przedziałów neutralnych.

7. Symbol statystyczny konkretnego wyrobu ( 2454 - 411 ) zawarty w ................. oznacza, że produkt ten został wytworzony przez : a) przemysł spożywczy.

8. Kryterium podziału paneli na statystyczną i dynamiczną jest: c) skład uczestników panelu.

9. Która z niżej wymienionych form pomiaru bezpośredniego charakteryzuje się największym poziomem głębokości : b) metody projekcyjne i c) wywiad grupowy.

10. Następujący schemat eksperymentu A/EM/ : P1 x P2 jest eksperymentem : a) jednogrupowy z dwoma pomiarami .

11. Najłatwiejsze do zliczenia są dane uzyskane z odpowiedzi : d) wyskalowanych.

12. Obliczanie średniego /standardowego/ błędu szacunku średniej arytmetycznej koniecznie jest gdy : a) liczebność próby jest mniejsza niż 30.

13. Jednym z podstawowych warunków zastosowań metod ekstrapolacyjnych w prognozowaniu jest możliwość : a) określenie sposobu kształtowania się danego zjawiska w przyszłości .

14. Jeżeli wyniki badania nie przyczyniają się do całkowitego rozwiązania określonego problemu lub decyzji to badanie określa się jako: a) źle zaprojektowane /niedostosowane/.

15. Główne czasopismo teoretyczne traktujące o badaniach marketingowych w Stanach Zjednoczonych zatytułowane jest „Journal of Marketing Research„ wydawane jest kwartalnie przez : a) AMA .

Seria 4

1. Wiadomo że proces badań marketingowych jest procesem cyklicznym. Takim samym procesem cyklicznym jest również: c)badania konkurencji

2. Wszystkie formy pomiaru wyodrębnia się zgodnie z kryterium drogi przepływu danych od ich źródła do badania. Wszystkie ankiety zalicza się do pomiarów: c)pierwotnych sondażowych pośrednich

3. Wraz z rosnącą wielkością próby i rosnącą ilością prób dobranych metodą losowania prostego: d) prawdziwe jest zarówno twierdzenie A jak i C

4. Pomiar porządkowany nie daje informacji o wielkości kolejnych różnic między przedziałami. Przyczyną tego stanu rzeczy jest: b) brak jednostki miary

5. Pytanie otwarte charakteryzuje się tym, że odpowiedź na nie jest odpowiedzią: c) całkowicie swobodną

6. Zastosowanie jednolitych skal intensywności (skal porządkowych) opisanych werbalnie za pomocą pięciu kategorii jednakowych dla każdego badanego przypadku jest charakterystyczne dla skal: d) Likerta

7. Z której nomenklatury towarowej stosowanej w handlu międzynarodowym pochodzi nr statystyczny o symbolu 735.91: d)SITC

8. Która z niżej wymienionych form pomiaru pośredniego zapewnia respondentowi osobistą anonimowość: d) ankieta prasowa

9. Decyzję o wyborze wywiadu prostego standaryzowanego podejmuje badacz wówczas, gdy: d) wymienione wyżej czynniki są spełnione jednocześnie

10. Eksperyment jednogrupowy z serią pomiarów ma największe zastosowanie do oceny wpływu: e)dotychczasowej tendencji w zakupach na politykę reklamową firmy

11 .Najbardziej poprawna logicznie i najłatwiejsza do interpretacji jest tablica dwudzielna obejmująca dane pochodzące: a) tylko z odpowiedzi rozłącznych

12. Średnia liczba pracowników zatrudnionych w firmach zagranicznych(w tym polonijnych) w Polsce w roku 1986 oszacowana na podstawie pomiaru 400 elementowej próby, z której średnio 300 zatrudnionych, a odchylenie standardowe s 200 przy poziomie ufności 93.445 dla którego t=2: c) 280-320

13. Przy współrzędnych (t₁,y₁), (t₂, y₂),...,(t_n, y_n) w układzie równań w metodzie najmniejszych kwadratów określają: c) poszczególne pomiary

14. W najpewniejszy sposób badacz bierze udział w zastosowaniu wyników badania w praktyce, gdy występuje w roli: d)członka kadry kierowniczej

15. Badanie ankietowe przeprowadzone w wielkiej Brytanii w 1984 r wykazało, że procent przedsiębiorstw prowadzących badania we własnym zakresie ..... zalecają je agencją badawczym wynosi: c)62

SERIA 5

1. Klasyfikacja badań marketingowych przeprowadza się według różnych kryteriów. Najbardziej rozbudowana jest klasyfikacja według zasady: a) przedmiotu badania.

2. Plan badania opinii klientów sklepów wolnocłowych „Baltony” został opracowany przy zastosowaniu: e) metody PERT

3.Wzrost liczebności próby polepsza precyzję estymatora, ale wielkość próby: a) nie zależy od wielkości populacji.

4. Budowa skali jednobiegunowej polega na tym, że przy danym jednym biegunie drugi jest jego: a) negacją

5. Pytanie zamknięte charakteryzuje się tym, że odpowiedź na nie jest odpowiedzą: e) wyskalowana

6. Pomiar wieloczynnikowy ma największe zastosowanie do:

a) testowania nowego produktu

7. Przedmiotem pomiaru wtórnego są:

e) wyniki pomiarów pierwotnych lub wtórnych

8. Która z niżej wymienionych form pomiaru pośredniego zapewnia ankieterowi największą kontrolę: c) ankieta audytoryjna

9. Testy obrazkowe są instrumentami pomiarowymi w ramach metod: a) konstrukcji

10. Podstawowym zadaniem grupy kontrolnej w eksperymencie jest: b) wyodrębnienie i określenie niektórych źródeł błędów

11. O poprawności logicznej każdej klasyfikacji decyduje przede wszystkim: d) zasada zupełności i rozłączności jednocześnie

12. Standardowy błąd proporcji dla p=0,50 szacowanej z próby n=26 wynosi: b) 0,10

13. Metoda średnich ruchomych /absolutna/ jest stosowana do celów prognozowania wówczas gdy zebrane dane charakteryzuje trend liniowy a wahania sezonowe są: e) addytywne i o stałej amplitudzie

14. Ochroną prawną w zakresie badań marketingowych objęto:

c) klientów, respondentów i firmy badawcze

15. Największą firmą badawczą w Wielkiej Brytanii jest: d) AGB

SERIA 6

1. Największa organizacja na świecie zrzeszająca członków badaczy indywidualnych: AMSO

2. Najstarsze czasopismo w Europie: JMRS

3. W skali nominalnej zmienne z jednej lub dwóch prób niezależnych, szacowana jest za pomocą testu: b) γ²

4. Kiedy można stosować eksperyment w formie kwadratów Tacińskiego: Każda z dwóch zmiennych ograniczających podzieloną na jednakową liczbę grup

5. Wczesnym symptomem wzrostu popytu w gospodarce jest: zwiększona liczba kupowanych dóbr komplementarnych

6. Co jest jednocześnie źródłem pierwotnym i wtórnym: folder

7. W skali przedziałowej miary przejęte są jako: arbitralne

8. Jaka skala stosowana jest do pomiaru preferencji: skala somatyczna

9. O czym decyduje wybrana metoda pomiaru preferencji: o reprezentywności

10. Do jakiego rodzaju instrumentów pomiarowych zalicza się skaner: mechaniczne

11. Co musi uzyskać badacz od uczestników wywiadu grupowego, aby badanie mogło być przeprowadzone: niewymuszona zgoda

13. Jakie cechy świadczą że jest to test rysunkowy: chmurki i dymki; czym się różni: lepiej wykorzystuje metody projekcyjne

14. Kwestionariusz testowany jest za pomocą: wywiad osobisty lub telefoniczny

15. Pojemność rynku: pojemności wtórne

SERIA 7

1. International Trade Forum. - wydaje UNCTAD - GATT.

2. Marketing Sales Management - wydaje Index Siły Nabywczej

3. Informacja odebrana przez człowieka i interpretowana - kiedy dane zamieniają się w informacje.

4. Zadanaie na wzór -

5. Trafność daje - błędy systematyczne.

6. Metody projekcyjne - Instrument Test.

7. Jaki program komputerowy ma mój odział (firma bad.) w Krakowie - SPSS

8. Porządkowa skala - Test K-S

9. Jakiego rodzaju skalowanie zosyało zastosowane: 1-entuzjastyczne, 2-b. pozytywne,3-pozytywne, 4-obojętne,5-negatywne Odp: Skala niezrównowazona.

10. Przed rozpoczęciem pomiaru wybiera się metody analizy danych, użyteczną metodą umożliwiającą dobór sposobów analizy jest: Pomiar imitacyjny z użyciem wstępnie zaprojektowanych instrumentów.

11. Eksperyment z grupą .. Eksperyment rzeczywisty.

SERIA 8

1. Elastyczność sprzedaży, udział w - jakie badanie: A - okresowe

2. Poziomy pomiaru - Stevens

3. Tachioskop służy do pomiaru - Ruchu gałek ocznych.

4. 7 cech - 0,5(n(n-1))= 0,5*7*6=21

5. Zadanie na wartość D (015)

6. Wydawnictwo Intligent Unit - Quartal Economic Review

7. Najlepszy poziom kontroli w ankiecie - Audytoryjnej.

8. Tabulacja - wielodzielne

9. Efekt febry - wszystkie.

10. Wywiad internetowy - CAWI

11. Warunki prowadzenia dalszych czynności badawczych jest .. w tym stadium twierdzenia - wartość wytworzonej informacji będzie większa od kosztu jej wytworzenia.

12. Manipulowanie modelami eksperymentalnymi w celu .. - Symulacja

13. Netoda wejść - wyjść - Bilans przepływów miedzygałęziowych

14. Suma 100% - D kołowy

15. Połączenie scentralizowanych i zdecentralizowanych - Zintegrowane lub mieszane.

SERIA 9

1. Rodzaj badań marketingowych… - Okresowe

2. Zadanie: 25%

3. Która z podanych poniżej organizacji .. - International Yellow Pages.

4. Jaka jest różnica pomiędzy skalami złożonymi nad skalami proztymi - wszystkie pozytywne.

5. Badania w 1984 wykazały, że udział wydatków w rocznej sprzedaży .. - Mniej niż 0,5%.

6. Tablice są łatwiejsze do zapamiętania kiedy ich.. - od 15% - 20%.

7. Z czym mamy do czynienia, gdy warunki próby uogólniamy dla całej populacji - wnioskowanie statystyczne.

8. W jakiej formie zbiera się dane w komputerze, aby je można było zliczyć

9. Jaki test stosuję się w celu weryfikacji .. wielkościami empirycznymi .. a wielkościami szacowanego skala interwałowa i stosowana gdy liczebność<30 - Test T-Studenta.

10. Kiedy mamy do czynienia z obserwacją uczestniczącą - wejście do określonej grupy.

11. W jakiej metodzie prognozowania mamy do czynienia z indeksem siły - Metoda symptomów.

12. W analizie przyczyny odmowy udziału w .. było - Nieodpowiedni czas.

13. W programie sieciowym badania o najdłuższym czasie - ścieżka krytyczna.

14. Przedmiotem pomiaru jest - cecha.

SERIA 10

1. Do jakiego rodzaju badań zalicza się badania konkurencji wg kryterium przedmiotowego - d) otoczenia krajowego i zagranicznego.

2. Do jakiego rodzaju błędów zalicza się różnicę między danymi niezbędnymi do rozwiązania określonego problemu decyzyjnego, a danymi poszukiwanymi przez badacza - c) problemu badawczego.

3. Jednostka próby może być jednocześnie elementem populacji badanej. Element populacji jest zwykle jednostką naturalną, np. - e) produkt.

4. Która z niżej podanych, skróconych definicji popytu jest najbardziej zbliżona do operacyjnej definicji popytu - a) popyt jako ilość towaru.

5. W ramach stosowanej metody odpowiedzi losowych zadano respondentowi 2 pytania A - czy dokonał kradzieży , B - Czy urodził sięw maju. Zakładając że mechanizm losowania to rzut monetą … odp -e) 10%

5. Która skaal jest głównym elementem złożonej skali pozycyjnej - b) nominalna.

7. Która z niżej wymienionych ksiąg adresowych jest wydawana przez GUS -a) REGON

8. Co zalicza się do głównych zalet ankiety pocztowej - d) to, co w punktach B i C

9. Jakim skrótem oznaczono w europie system zunifikowanego kodu produktu - e) EAN

10. Jakimi wymiarami charakteryzuje się eksperyment w postaci modelu czynnikowego - e) wszystkimi wymienionymi

11. Jakim skrótem okresla się skomputer. Przeprowadzania wywiadów - e) CAPI

12. W roku 1995 sprzedano towarów za 50 mln, a w roku za 95 mln. Ile wynosiło średnioroczne tempo wzrostu sprzedaży tych towrów w latach 95 - 99 ? - c) 18%

13. Odmiana jakiej metosy jest metoda analogii historycznej jako jakościowej metody prognozowania? - b) przypadków

14. Kiedy stosuje się wykresy liniowe? - e) gdy wystapi jakakolwiek wyżej wymieniona sytuacja

15. która z wymienionych firm amerykańskich ma największe dochody spoza granic USA? - E A.C. Nielsen

SERIA 11

1. W Europie pierwszym czasopismem na temat badań rynkowych wydawanym od 1958 było - d) Jurnal of Buisness Research.

2. Do której z niżej wymienionej grup metod zbierania danych należy ankieta internetowa - d) sondaży pośrednich.

3. Jak nazywają się składowe ilości jednostek próby podzielone proporcjonalnie do udziałów poszczególnych warstw w badanej populacjii - b) kwotami

4. Jak nazywa się definicja zawierająca zalecenia służące pomiarowi definiowanej cechy - e) operacyjna.

5. Czym charakteryzują się pytania, które wszyscy respondenci rozumieją i interpretują jednakowo - e) jednoznacznością.

6. Jak nazywa się pomiar dotyczących wielu powiązanych ze sobą cech jednego produktu preferencji respondentów - b) pomiarem wieloczynnikowym.

7. Do której nomenklatury towarowej należy kod statystyczny 1053-122 - SVW

8. W której z niżej wymienionych ankiet ankieter bierze bezpośredni udział - a) audytoryjna.

9. Do jakich pomiarów używa się tachioskopu oraz wideo kamery sprzężonej z komputerem - C pomiarów fizjologicznych.

10. Który z niżej wymienionych modeli eksperymentów zastosowałbyś w celu zidentyfikowania wpływu zmiennej eksperymentalnej na tendencję w sprzedaży - d) dwugrupowy z 4 pomiarami

11. Jakim symbolem oznacza się skomputeryzowane wywiady osobiste - c) CAPI

12. Który z niżej wymienionych testów służy do weryfikacji wyników z pomiaru porzadkowego -e) test K - S

13. Jak nazywa się ranking oceny metod zbierania danych ze względu na etykę związaną z tym postępownaiem - d) system Wade'a

14. Kto jest włąścicielem największej na świecie firmy badawczej A.C. Nielsen - c) Dun&Broadstreet.

15. Jak nazywaja się badania polegajace na regularnym zbieraniu danych, analizie i udostepnianiu ich - d) sydykatowe.

SERIA 12

1. Przez kogo został założony pierwszy dział marketingowy w 1911 w firmie The Curtis publishing Company - b) Parlinba

2. W przypadku planowania planowania bardzo skomplikowanych i długotrwałych badań mark. Stosowąc należy metodę plan. Sieciowego. Która z metod pozwala na planowanie i określanie kosztów - a) PERT

3. która z poniżej wymienionych skal pomiarowych ma umowny ponkt zerowy - b) jednostkowa

4. Który rodzaj pytań pozwala na ograniczenie błędu związanego ze zdolnością respondenta do odpowiedzi - c) pytania filtrujące

5. Jak nazywa się założona skala postaw składajaca się z kilku lub kilkunastu siedmiostopniowych skal porządkowych, z których każda jest na biegunach antanonimami - a) skala semantyczna.

6. Do jakiego rodzaju źródeł informacji zaliczamy opakowania produktów konkurencyjnych - a) zewnętrznych źródeł pierwotynych.

7. W której z niżej wymienionych pośrednich metod zbierania danych może mieć zastosowanie w pełni reprezentatywna próba losowa - d) ankieta pocztowa.

8. Z badań prowadzonych systematycznie przez firmę Walker Research w usa wynika … - d) wywiad grupowy.

9. Do której grupy eksperymentów zalicza się ekspeyment w postaci modelu czynnikowego - d) statystycznych.

10. jaką literą oznacza się największą różnicę między warościami skumulowanymi … w teście K - S - b) wartość H

11. Do której grupy metod, prognozowania zalicza się metody wczesnych symptomów - b) przyczynowo - skutkowych

12. Jaką metodę graficzną należy zastosować w raporcie gdy dane odzwiercedlają kilka zjawisk jednocześnie … - c) wykres liniowy.

13. jakiemu problemowi przeciwstawiane jest prawo do poszukiwania obiektywnej prawdy w zakresie etyki badań marketingowych-c) wymuszonej zgody respondent

14. Kto jest właścicielem najwirekszych na świecie firm badawczych A.C Nielsen i IMS International - c) Dun&Bradstreet

15. która z niżej wymienionych polskich firm badawczych ma swoją siedzibe w Gdańsku - c) Eurotest.

Seria 13

1.Jaka firma nie należy do zrzeszenia CASRO - Gallup

2.Weryfikacja porządkowa - test K-S

3.Czego dotyczy krzywa poligraficzna - pomiary fizjologiczne

4.Co to jest ruch gałek ocznych, pomiary fal mózgowych - pomiary fizjologiczne

5.Badania cykliczne - badania konkurencji

6.Skomputeryzowane badania telefonicznych wywiadów - CATI

7.Zadanie na wzór: - 40

8. Czego nie obejmuje pomiar kwotowy - metod statystycznych

9.Która metoda jest najbardziej pogłębiona - wywiad grupowy

10.Co zastosować gdy wykres jest nieczytelny -

11. Które z badań wychodzi do decydenta - sporadyczne

12. Jak przejść od problemu decyzyjnego do badawczego -

13. Który z modeli zastosowałbyś w celu identyfikacji wpływu zmiennej eksperymentalnej na tendencję spadku - model dwugrupowy z serią pomiarów

14. Ekstrapolacja czego dotyczy, na co wpływa - punkt zwrotny

15. Problem z towarem, co jest powodem - różnica kwalifikacji towaru

Seria 14

1. Zadanie na obliczenie wartości D w teście K-S

2. Instytucja w USA zrzeszająca tylko firmy badawcze - CASRO

3. Kto wydaje Industry Image Study - Walker Reasearch

4. Ze znajomości metod prognozowania, metod ekstrapolacji (tab. Str. 370)

6. Kto napisał pierwszą książkę o badaniach marketingowych „ Principels” - Dunkan

7. Badanie w którym poddaje się pomiarowi wszystkie składniki jednostki to - badanie wyczerpujące

8. Próbka do pomiaru próbnego dotycząca kwestionariusza ... waha się - od 12 do 30 jedn.

9. Jaką skalę przed. stosuje się najczęściej wg badań Genterga Goldstechera - somatyczna

10. Proporcje i odsetki to wskaźniki struktury

12. Kto prowadzi badania grupowe - moderator

13. Jaka metoda losowa jest najbardziej adekwatna do doboru dużych prób z dużych wyrobów - losowanie systematyczne

14. Metody wątpliwe etycznie - bezpośrednie obserwacje z ukrycia lub w tajemnicy

15. Gdzie można ekstrapolować -

Seria 15

1. Która z firm w Polsce w 1999 była największa - GFK

2. Czego dotyczy krzywa poligraficzna - fizjologia

3. Która z metod BBO zakłada < im grupa jest mniej chętna na udzielanie odp., tym większego błędu należy oczekiwać - ekstrapolacji

4. Co zostało uznane za najbardziej nieetyczne w stosunku do badań AkAAh - lustro weneckie

5. Która ze skal może wyrażać temperatury i daty - przedziałowa? Interwałowa

6. Zadanie próba n=26, p=0,5 - 0,1

7. Które pytanie daje respondentowi możliwość odpowiedzi - zamknięte, otwarte???

8. Coś o nomenklaturze

9. Podstawowym kryterium podziału metod postępowania w badaniach marker. -

10. Zadanie 100 przedsiębiorstw 60 przeprowadza badania - błąd 4,9

11. Z czego korzysta przedsiębiorstwo by uzyskać dane o udziale klientów, produktów -

12. Do jakiej grupy zalicza się metodę wejścia - wyjścia - przyczynowo skutkowa

13. Coś o analizie porównywalności

SERIA 16

1. W którym roku Europa prześcigneła USA w wydatkach na badania marketingowe? - 1987

2. Która firma badawcza ma najwieksze obroty w Polsce w 1999 ? - SMG/KRC Poland

3. Jaki wykres przedstaewia rozkłady jakiegoś zjawiska w sumie daje 100%? - kołowy

4. Przy jakiej ankiecie ankieter ma bezposredni udział ? - Audytoryjna

5. jaki rodzaj błędów powstaje w wyniku zbierania złych danych/ - Błąd problemu badawczego

6. Jak nazywa się kompleksowe zabezpieczenie, które kosztuje 90 tys do 2 mln 250 tys? - audyt bezpieczeństwa.

7. minimalna liczeboność próby dla poziomu ufności 0,95 i jeszcze jedna dana ? - 100

8. Grupą jakich skal jest skala semantyczna? - porządkowych

9. W internecie jak się nazywa coś co ma bazy danych? - wyszukiwarka

10. jaki test stosujemy dla pomiarów porządkowych z wieloma zmiennymi? K-S abo ANOVA

11. Jaka technika wykorzystuje wycinki z gazet, urywki ? - kolażowa

12. Ile liczb może mieć nazwa zmiennej w programie SPSS - 256

13. Jak to definicja popytu „Ilość towaru …” - operacyjna

14. Jak nazywa się pytanie pomocnicze związane ze zdolnością trespondenta do odpowiedzi ? - filtrujące

15. Pomiar Salomona - 4 grupy z 6 pomiarami.

SERIA 17


1. Jaki jest test do zmiennych podziałowych? - t-Sudenta.

2. Ile przedsiębiorstw stosuje badania marketingowe (przykład)? - <0,5

3. Do Jakich badań zaliczamy badania rynku i badania konkurencji dystrybucji? - Ciągłych

4. Która z ksiąg ma charakter ogólny? - Yellow Book(Pages).

5. Wzór na kobiety w ciąży (25%)

6. W jakich netodach, gdy zapas jest równy zero to tworzą ścieżkę krytyczną? - metody PERT

7. odp. - wczesnych symptomów.

8. w którym roku Europa dogoniła stany w kosztach przeznaczonych na badania marketingowe? - 1987

9. odp. - 88 - 90

10. Do uogólnienia wyników z badań próby na całą populację? - wnioskowanie statystyczne

11. Co trzeba zrobić by lepiej zapamiętac tabelę w tekście? - zmniejszyć ja o 15 - 20 %

12. odp. - cecha (pierwotne), wtórne (dane)

13. odp. - wyeliminować

14. Jak nazywamy dane programu zakodowane i gotowe do analizy ? - plik

15. Dlaczego powstają badania kontrolne rynku?

SERIA 18

1. Pośrednikiem między badaniem marketingowym a użytkownikiem w MSI jest? - informatyczny system zarządania.

2. Wyniki rzetelne są pozbawione? - błędów przypadków

3. Jaki to rodzaj instrukcji w kwestionariuszu „Jeżeli nie proszę przejść do następnego pytania” - instrukcje kierujacego procesem pomiaru.

4. Jakie pytanie nie jest pytaniem decyzyjnym ? - o konkurencji.

5. MDS do czego służy? - dotyczy preferencji w percepcji nabywców (skalowanie wielowymiarowe)

6. Najtańszy nośnik - czy najmniejszy do przechowywania danych - najtańszy CD-ROM najmniejszy dysk optyczny.

7. Badacz zwraca się do respondenta z prośba aby ten wyobraził sobie drzwi produktu? - test zwirciadła.

8. Stała grupa respondentów ? - panel

9. Test K-S oblicz ??- 0,1

10. Test ufność 99,9 odchylenie stnd. 2,72 bład c=1 odp -

11. Badanie kontrolne w warunkach naturalnych służą do ? - do eksperymentu

12. Nośnik infometri telemetrii - terminale stacjonarne.

13. Jaki wykres najlepiej przedstawi - rozwój kilku wielkości w czasie we wzajemnych zmieniających się z okresu na okres relacjach? warstwowy

14. Problem wymuszonej zgody respondenta prawo do zachowania tajemnicy jest przeciwstawiane - prawo do poszukiwańia obiektywnej prawdy.

15. Największa firma badawcza w Polsce w 1999r - Pracownia Badań Społecznych.

SERIA 19

1. O gazecie

2. Ile wynosi grupa interwałowa, produkcja 5100,próba 170

4. Jakie badania przeprowadza poligraf - pomiar wrażliwości skóry

5. Coś o korelacji - metoda diagnostyczna

6. Jakieś pytanie, że coś cię dzieje wg. Czegoś - m. Scenariusza

8. Jakie największe badania przeprowadza się w Polsce

9. Jakie najnowsze w USA

11. Ile grup kontrolnych ma badania symulacyjne - 0?

12. Co stosuje się na sympozjach - ankieta audytoryjna

13. Jak nazywa się czynność wprowadzania do komputera?

SERIA 20

1. Co spowodowało rozwój bad. Marketingowych w latach 1970-1980 - d) teoria konsumenta

2. Załóżmy, że wylosowano próbę 100 przedsiębiorstw związanych z handlem zagranicznym, z których 20 prowadzi jakieś badania marketingowe. Z jakim błędem należy się liczyć - a) 4

3. Czy inflacja jest spowodowana rosnącym popytem, czy wysokimi kosztami. Dane są odpowiedzi: inflacja, jednym i drugim, kosztami. - trudna terminologia

4. Firma, której siedziba mieści się we Francji, znajdująca się na liście 25 największych firm badawczych na świecie - b) IPSOS Group S.A.

5. Wewnętrzna zgodność instrumentu pomiarowego można uzyskać dzięki metodzie - b) połówkowej

6. Ankieta, która jest powszechnie dostępna to - c) ogólna

7. kto wprowadził test plam atramentowych - b) Rorschach

8. Oprogramowanie służące jako okno na internet i punkt startu do wszystkich rozpoczynających się w nim operacji - b) przeglądarka

9. Gdzie występuje równocześnie skala rangowa i porządkowa - swobodnych ocen?

10. Dzięki jakiej skali można porównać dane jakościowe i ilościowe

11. Coś o zliczaniu danych a)wyskalowane

12. jaki bład można popełnić, gdy przedłuża się zbieranie danych - a)zmiana składu danych

13. Jeśli zadane pytanie ma związek z postawą wcześniej hipotezą - opisowe

14 Coś o raporcie, gdzie znajduje się opis metod - a)w treści głównej

S©. Pytania otwarte są pytaniami: nie vy skalowanymi

51. Cykliczność badań polega na tym, że: użytkownik informacji (decydent) jest zarówno
punktem wyjścia jak i etapem końcowym badania

52. Skala pięciostopniowa i opisana werbalnie to: pięć przedziałów i opis werbalny np.
Bardzo duży - duży - średni - mały - bardzo mały

53. Badania ankietowe. W.Brytania 1984r. wykazały, że jaki % przedsiębiorstw prowadzi
badania we własnym zakresie lub zleca agencjom badawczym: 62%

54. W miarę wzrostu liczebności próby: polepsza się precyzję estymatora przy wzroście

kosztów badania
56. Eksperymant jednogrupowy z serią pomiarów stosuje się: do eksperymentów z

udziałem paneli konsumentów

56. O poprawności logicznej w klasyfikacji świadczy: zasada zupełności i rozłączności

57. Metody wprowadzania poprawek i uzupełnień:

nie należy wymazywać danych orginalnych

sprzeczne lub niezgodnedane należy zmienić lub odrzucić

w niektórych przypadkach redaktor może określić odpowiedz

tam gdzie jest to konieczne, redaktor może wstawić dane szacunkowe

w przypadkach szczególnie ważnych podejmuje się próby ponownego kontaktu z

respondentem

dodatkowe uwagi lub komentarze

pytania pozostawia się bez odpowiedzi jeżeli zawiodą podane metody

58. Średnia ruchoma stosowana jest: w programowaniu trendu liniowego wahań
sezonowych o stałej amplitudzie

59. Plan badania opinii publicznej to: demoskopia
6Q. Skala jednowymiarowa: wynik można ująć w postaci jednej liczby lub prostego
jednowymiarowego wykresu

61. Skala wielowymiarowa: kompleksowa, składająca się z wielu skomplikowanych
matematycznych technik:

metoda skalowania wielowymiarowego (MDS)
metoda pomiaru wieloczynnikowego

62. Analiza tabulacyj na:

tabu lacja prosta (jedna zmienna)
tabulacja złożona (dwie i więcej zmiennych, {.dwudzielna, t.n-dzielna)

63. Odpowiedz na pytanie otwarte, to odpowiedz: niewyskalowana

64. Eksperyment z jednej grupy dotyczący wielu pomiarów to: panel konsumencki

65. Metody pomiaru sondażowego różnią się: anonimowością i stopniem kontroli pomiaru
(na poczucie anonimowości ma wpływ stopień kontroli pomiaru)

66. Ekstrapolacja to: ilościowe przedłużanie dotychczasowych tendencji na pewien okres
w przyszłości

67. Potencjalne błędy pomiaru:

wpływ pierwszego pomiaru

wpływ czynników nie kontrolowanych

reakcja respondentów

wpływ instrumentu pomiarowego

zmiany składu prób

niewystarczający czas pomiaru

68. Jaka organizaja wydała IMR? (loumal of Marketing Rescarch) AMA - American
Marketing Associacion

69. Kto stworzył definicję badań marketingowych:

„funkcją badań marketingowych jest dostarczanie informacji w celu wsparcia kierownictwa

przedsiębiorstw trafnych decyzji"? defwg D.I. Hawkins i D.S .Tuli
" systematyczne projektowanie, zbieranie, analizowanie i prezentowanie danych i wyników
badań związanych istotnie ze specyficzną sytuacją marketingową przedsiębiorstwa" def. P.

Kotler

„Badania marketingowe wiążą daną organizację z jej rynkowym otoczeniem. Organizacja
projektu/obadania, gromadzi, analizuje i interpreyuje dane, aby pomóc kierownictwu w
zrozumieniu otoczenia, zdefiniowaniu problemów i sprzyjających sytuacji oraz rozwoju i
przeprowadzeniu badań na określonych rynkach " def. D.Acker i G.Day

70. Ile wynosi kombinacja możliwości wyboru metod losowych i melasowych doboru prób?

*J6=32)

71. Za pomocą jakich środków prezentuje się użytkownikom wyniki badania zawierającego
instrukcje definiujące użyte instrumenty? Za pomocą konspektu

72. Jak nazywają się usługi polegające na regularnym zbieraniu danych, naokreslonym
analizowaniu ich? Syndteateehresearch

73. Która z metod szacowania BBOjest najbardziej efektywna? Metoda próbki z próby

74. Jaka gałąź gospodarki oznacza kod 2809 - ITMZ? Przemysł spożywczy

75. Co oznaczają liczby w kodzie kreskowym: 73100400113186? Numer produktu

76. Czynności odwzorowania mierzonej cechy za pomocą wybranej skali nazywa się:

skalowaniem.

76. Co to jest dobór próby? Jest to sposób w jaki elementy populacji badanej są wybierane z
tej próby

77. Co to jest problem decyzyjny? Jest on wówczas zidentyfikowany, gdy są ustalone cele, a z
aktualnego stanu rzeczy wynika, że cele te nie są jeszcze osiągnięte

78. Jaki jest pierwszy etap realizacji projektu? Jest tozbieranie danych ze źródeł
wtórnych.pozostała częśćdanych pochodzi ze źródeł pierwotnych.

79. Co się dzieje gdy badanie nie daje oczekiwanego rezultatu? Jest źle sformułowana
ankieta.
—&0. Cowplywa na zmianę wyników badania?

81. Kiedy oblicza się średnihłąd z hróby? Kiedy n > 30.

82. Co to jest pomiar? Pomiar polega na przyporządkowaniu określonych symboli do
mierzonychobiektów. Poziomy pomiaru są wyznaczone przez zastosowane skale naturalną,
porządkową, przedziałową i stosunkową.

83. Kiedy się stosuje skale nominalne? Stwierdzenie różności i równości, klasyfikacja
_?j^???.dzielna numeracja nie uporządkowanych decyzji.

84. Jakie pytania zawarte w kwestionariuszu najlepiej się zadaje? Zamknięte i wyskalowane

85. Jak wygląda skala semantyczna? Jest ona zestawem kilku lub kilkunastu skal
porządkowych. Umożliwia pomiar postaw, zbieranie oraz analizę danych.

86. Nomenklatura ITHZ? Przemysł spożywczy. ^c

87. Co to jest, gdy problem porównywalności dostępnych cech występuje wówczas, gdy
badacz ma do czynienia z wywiadem bezpośrednim, klasyfikacjami towarów w statystykach

międzynarodowych oraz w statystykachJ^ZzagranicznegoposzczegółnycHkrajów^
KLASYFIKACJA TOWARÓW ^~^^c * ^, ./

89. Podział paneli ze względu na skład uczestników:

statyczne

dynamiczne

89. Dane o rysunkach zbierano już w średniowiecznej Europie, czego dowodem było m.łn. to,
ze każdy z domów dysponował własną służbą informacyjną. Działalność tych służb dała
początek PIERWSZYM GAZETOM.

90. W warunkach definiowania problemu badawczego najważniejszą w.s f ępną czynnością

badacza jest ścisłe określenie: problemu decyzyjnego.

91. W praktyce isnieje pewna maksymalna ilość metod doboru losowego i melasowego prób.

Ta max. liczba wynosi: 32.

92. Czynność odwzorowania mierznej cechy przy pomocy wybranej skali to: skalowanie

92. Układając pytania kwestionariuszowe należy dążyć do ich jednoznaczności.

Jednoznaczność oznacza, że: wszyscy respondenci rozumieją pytania jednakowo.

94. Wynikiemanalizy danych zebranych przy pomocy skali semantycznej jest zwykle obraz

graficzny. Zestaw lini nazywa się: profilem polaryzacji.

9.5-. Problem porównywalności dostępnych danych występuje w statystykach

międzynarodowych wówczas, gdy mamy do czynienia z różnymi klasyfikacjami towarowymi.

96. Jeżeli po upływie pewnego czasu część respondentów odmawia udziału w eksperymencie

lub następują inne nieprzewidziane zmiany naturalne, to mówimy że błąd spowodowany

został: zmianą składu prób.

97: Poza konkretnymi metodami dokonywania poprawek i uzupełnień należy przestrzegać

pewnych zasad ogólnych poprzez: stosowani wszystkich podanych pomiarów jednocześni e.

98. Metody ekstrapolacyjne wykazują niewielkie możliwości w przewidywaniu: punktów
zwrotnych, w których tempo wzrostu lub spadku, gwałtownie się zmienia

99. Wzory i kopie użytych w badaniu instrumentów pomiarowych (konwencjonalnych)
najlepiej jest zaprezentować słuchaczom z wykorzystaniem: konspektu.

100. Która metoda ankiety daje największą kontrolę? Ankieta bezpośrednia.

707. Jaki jest wpływ grupy kontrolnej w eksperymencie?

102. Do jakich metod należą testy obrazkowe? Metod konstrukcji.

J ffi3'. Co jest przedmiotem pomiaru wtórnego?

Przedmiotem pomiaru nie jest osoba, rzecz, stan czy zdarzenie lecz cechy wymienionych

kategorii. Cecha danej rzeczy jest ?to co orzeka się o przedmiocie, odpowiadając napytanie

jaki on jest. "ⁿ -1 Y).

104. O poprawności logicznej w klasyfikacji świadczy:

Przy klasyfikacji odpowiadzi napytania otware stosuje się te same zasady logiczne jak w
przypadku skalowania odpowiedzi na pytania zamknięte . W przypadku pytań otwartych zasdy
te jest trudniej zastosować. Są to zasady zupełności i rozłączności.

105. Najobszerniejszym kryterium przy klasyfikacji rodzajów badań marketingowych jest:

kryterium przedmiotowe.

106. Do czego służy pomiar wieloczynnikowy? Polega na pomiarze preferencji respondentów

względem kilku powiązanych ze sobą czynników (cech) jego produktów. Ma on główne

zastosowanie do testowania nowych roduktów i środków reklamy. Rezultatem pomiaru i

analizy są dane tworzące skale przedziałowe.

107'. Do czego służy średnia ruchoma? <7

Do programowania trendu liniowego o wahaniu... ,

108. Kto ma ochronę prawną?

Respondenci, klijenci, grupy społeczne, firmy badawcze.

109. Na jakiej ulicy mieści się w Warszawie GUS? Aleja Niepodległości

77tt Jakie metody są najbardziej pogłębione? Metody projektowe.

777. Która z metod jest najgłębsza? Ankieta osobista

11-2. Kiedy stosujemy metodę ekstrapolacji? Istotą tej metody jest ilościowe przedłużenie

dotychczasowych tendencji na pewien okres w przyszłości. Metody te są efektywne w

programowaniu krótkookresowym.

113. Do której nomenklatury towarowej należy kod statystyczny o symbolu 1053-122? Do

SWW.

114 W której z niżej wymienionych ankiet ankieter bierze bezpośredni udział?

Andy tory jna

115. Do jakich pomiarów używa się tachistoskopu oraz wideokamery sprzężonej z
komputerm pomiarów fizjologicznych

116. Który z niżej wymienionych modeli eksperymentnów zostosowałbyś w celu
zidetyfikowania wpływu zmiennej eksperymentalnej na (endencję w sprzedaży)
dwugrupowy z serią pomiarów

117. Jakim symbolem oznacza się skomputeryzowane wymiary osobiste? CAPI

118. Który z niżej wymienionych testów służy do weryfikacji wyników z pomiaru
porządkowego? TestK-S

119. Jak nazywa się ranking oceny metod zbierania danych ze względu na etykę
związaną z tym postępowaniem? System Wadę 'a

120. Kto jest właścicielem największej na świecie firmy badawczej A.C.Nielsen? Dwi &
Bradstreet

121. Jak nazywają się badania polegające na regularnym zbieraniu danych, analizie i
udostępnianiu ich zainteresowanym klikantom? Panelowe / Sydykatowe

122. Decyzje o wyborze wywiadu ???? wówczas gdy: -? p^e^o , ^0^^^^^ '2-
d)wymierzonewyżej czynniki muszą być spełnione jednocześnie
- 1Z3J? jednogrupową z( serią) ? za największe zastosowanie do ? wpływef
f e) dotychczasowej tendencji w ?na polityką reklamową firmy, ^^j
'^pc - 124. Najbardziej poprawna logicznie i najłatwiejsza do interpretacji jest ..zbalacja dwud,. Z
''•yW objaśniająca dane pochodzące : '^ł&1

a) tylko z odpowiedzi rozłącznych

125. średnia liczba pracownikówJZ.w firmach zagranicznych / tzw. Polonijnych/ w Polsce w
roku 1985 oszacowana na podstawie pomiaru 100 elementowej próby, w której średnia 300
zatrudnionych, odchylenie standardowe s = 200 (przy poziomie ufności 95,445 ) dla którego
Z(alfa) == 2, wyniosła:

b) 280 - 320 str. 89

126. Pary współżędych ........... układa również w metodzie najmniejszych kwadratów

określają:

^B c) poszczególne po...

127. W najpełniejszy sposób badacz bierze udział w zastosowaniu wyników badania w

praktyce, gdy występuje w roli:

d) członka kadry kierowniczej

HlL-Badanie ? przeprowadzone w Wielkiej Brytani w roku 1984, wykazało że procent

przedsiębiorstw prowadzących badania we własnym zakresie lub zlecających je agencjom

badawczym wynosi:

c) 62%

129.Informacja jest stanem niematerialnym, nie jest ani energią ani materią. Jej przeniesienie

może się odbywać pod warunkiem że:

a) zostanie użyty zmysł wzroku

b) przybierze ona określoną postać fizyczną w formie nośnika

c) określi się dokładnie jej granice występowania

d) zostanie przekazana przez nadawcę do adresata

e) wystąpi w czystej postaci poza systemem nerwowym człowiek

130, Jeżeli nastąpi różnica między wynikami przekazanymi przez badacza a informacją
odebraną przez użytkownika to jest to błąd:

a) prezentacji wyników analizy

b) problemu badawczego

c) pomiaru

d) wytypowania niewłaściwej populacji generalnej

e) analizy danych

131. Lista odwzorowująca wszystkie elementy badane populacji nazywa się:

a) wykazem

b) operatem losowania

c) zarówno wykazem jak i operatem

d) książką adresową

e) zupełnie inaczej

132. Podstawowym warunkiem konstrukcji instrumentu, zwłaszcza konwencjonalnego jest
dostosowanie odpowiednich skal do instrumentu oraz instrumentu do tych skal. Czynność ta
nazywa się:

a) przyporządkowaniem symboli cechom obiektu

b) cechowaniem instrumentu

c) wyznaczeniem poziomu pomiaru

d) skalowaniem instrumentu

e) zarówno skalowaniem jak i wyznaczeniem poziomu pomiaru

133. W ramach stosowanej metody odpowiedzi losowych zadano respondentowi dwa pytania
„Czy ukradłeś cokolwiek w tym sklepie w ostatnim miesiącu?" oraz „Czy urodziłeś się w
maju?". Zakładając że mechaniz losowania jekim jest rzut monetą daje równe sznse wyboru
pytania A i B, proporcja odpowiedzi łącznej na dwa pytania A i B wyniosła 0,2 a ze statystyk
spisu powszechnego wynika że 20 % mieszkańców urodziło się w maju - proporcja
twierdzącej odpowiedzi na pytanie pierwsze wyniosła:

.a) 20%

b) 25%

c) 30%

d) 35%

e) 40%

134. Każda składowa skali semantycznej jest zazwyczaj skalą dwubiegunową ograniczoną z
dwu stron parą:

a) rzeczowników
' b) anonimów

c) przymiotników

d) synonimów

e) wyróżników

135. Który z wymienionych niżej czynników decyduje o wiarygodności pomiaru wtórnego?

* a) trafność

b) rzetelność

c) solidarność

d) jakość

e) rządna z powyższych

136. Za najbardziej efektywną szacowania błędu wynikającego z braku odpowiedzi uważa
się:

a) metodę ekspoacji

b) metod

• c) próbki z próby

d) metoda szacowania subiektywnego

e) metoda porównywania ze znanymi parametrami

137. Jeżeli po upływie pewnego czasu część respondentów odmawia udziału w
eksperymencie lub następują inne nieprzewidziane zmiany naturalne, to mówimy że błąd
spowodowany został:

145. Załóżmy że respondent odpowiedział iż nigdy nie słyszał o danym produkcie podczas
gdy z odpowiedzi na inne pytania tego samego kwestionariusza wynika że używa on tego
produktu. Błąd tego rodzaju redaktor powinien zaliczyć do:

a) odpowiedzi nieadekwatnych

b) sprzeczności i niezgodności

c) odpowiedzi niekompletnych lub niejednoznacznych

d) pomiarów fikcyjnych

e) żadnego spośród wymienionych

146. Średnia arytmetyczna może być obliczona tylko z danych uzyskanych z pomiaru:

d) jednostkowego i proporcjonalnego(przedziałowe i stosunkowe)

147. Grupa specjalistów będących respondentami w pomiarze metodą delficką nazywana jest:

b) grupą ekspertów

148. Jak zapisałbyś liczbę 50,89 w raporcie?

a) 50,9b) 50,89c) 50,8 d) 51e) 51,0

149. Które spośród niżej wymienionych grup przedsiębiorstw są jednocześnie wykonawcami
badań marketingowych na zlecenie oraz zleceniodawcami tych badań?

a) firmy badawcze

b) przedsiębiorstwa wytwarzające dobra konsumpcyjne

c) przedsiębiorstwa handlowe i usługowe

d) firmy świadczące usługi finansowe
> e) agencje reklamowe

150. Problem porównywalności pewnych danych występuje w statystykach
międzynarodowych wówczas gdy mamy do czynienia z różnymi :

b) klasyfikacjami towarowymi

29

---