Badanie obwodów RLC
Celem ćwiczenia jest poznanie właściwości obwodu elektrycznego zawierającego elementy R, L i C oraz sprawdzenie podstawowych praw obwodów elektrycznych dla obwodów zasilanych prądem sinusoidalnie zmiennym.
Najprostszym jest obwód zawierający źródło napięcia sinusoidalnie zmiennego i idealny rezystor. (Rys.1)
Rys.1. Obwód R
Zgodnie z prawem Ohma mamy:
![]()
Dla rezystancji idealnej funkcje prądu i napięcia są zgodne w fazie czyli przesunięcie wynosi:
Δϕ=0
Drugim z tych obwodów jest obwód RL przedstawiony na rys.2 powstały poprzez szeregowe połączenie idealnego rezystora i cewki.
Rys.2. Obwód RL
Na podstawie II prawa Kirchhoffa zastosowanego do tego obwodu, otrzymujemy równanie:
![]()
na podstawie teorii równań różniczkowych otrzymujemy rozwiązanie, którym jest funkcja:
i(t) = Im sin(ωt+ϕ)
gdzie: 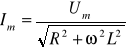
oraz
Można zauważyć, że jeśli R→0 wówczas ϕ→ zatem dla idealnej cewki napięcie wyprzedza funkcje prądu o kąt czyli:
![]()
Rys.3. Prąd i napięcie w obwodzie RL
Kolejnym elementarnym obwodem elektrycznym jest obwód RC przedstawiony na Rys.4.
Rys.4. Obwód RC
Równanie dla tego obwodu ma postać:
u(t)= ![]()
Rozwiązaniem równania jest funkcja
i(t) = Imsin(ωt+ϕ)
gdzie I m =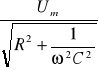
oraz
Zauważamy, że dla kondensatora idealnego R→0 oraz ϕ→.
Wynika stąd, że napięcie na okładkach kondensatora jest opóźnione względem funkcji prądu o kąt
czyli: ![]()
Rys.5. Prąd i napięcie w obwodzie RC
Rysunek 6 przedstawia szeregowe połączenie elementów RLC
Rys.6. Obwód szeregowy RLC
Z II prawa Kirchoffa wynika, że jeżeli w obwodzie płynie prąd sinusoidalnie zmienny, wówczas:
i(t)=Imsinωt
u(t)= uR(t) + uC(t) + uL(t)
gdzie: uR(t)= RImsinωt
uc(t)=Imsin(ωt-900)
uL(t)= ωLImsin(ωt+900)
po podstawieniu otrzymujemy:
u(t)=Im[R sinωt+(ωL-)cosωt]
u(t)=Umsin(ωt+ϕ)
gdzie ϕ = arctg
Um=Im
Podobnie możemy rozpatrzyć połączenie równoległe elementów R, L, C.
3
4
~
U(t)
R
I(t)
~
U(t)
R
I(t)
L
t
U(t)
i(t)
i(t)
U(t)
I
U
UR
UL
~
U(t)
R
I(t)
C
t
U(t)
i(t)
i(t)
U(t)
I
U
UR
UC
ϕ
~
U(t)
R
I(t)
C
L
U
IC
ϕ
UC
UR
UL
Wyszukiwarka