2) Stan wymuszony (c_o=0)

3) Stan mieszany (
)

4) Stan ustalony (t ∞)

C(∞) = c*

Rozmnażanie się kolonii bakterii (biomasa)

Przyrost biomasy dm(t)/dt = β t

β - współczynnik efektywnego przyrostu naturalnego

m(0) = m_o

m(t) = m_o e ^{( β t )}

β > 0 - więcej się rodzi niż umiera

β = 0 - tyle samo się rodzi co umiera

β < 0 - więcej umiera niż się rodzi

m (k + 1) = α m(k) pierwszy model dynamiczny w czasie dyskretnym

m (0) = m_o

k=0 m(1) = α m(0) = α¹ m_o

k=1 m(2) = α m(1) = α² m_o

m(n) = αⁿ m_o (* dyskretne)

dla t = m ∆t

(*) ciągła = (*) dyskretna

m_o e^{β ∆t n} = m_o αⁿ /

e^{β ∆t} = α

β = 1/∆t lnα

Model demograficzny

Rozkład wieku w populacji

Liczba ludzi w populacji w roku + liczba wieku

K lat N_t(k)

Jest to model KOHORT

N_{t + 1} (k+1) = β_k N_t (k)

(co roku stajemy się coraz starsi i przechodzimy do następnej kohorty)

0 < β < 1

N_t(0) = α₁ N_t (1) + α₂ N_t (2)+ … + α₂₃ N_t (23)+…

Systemy dynamiczne z czasem dyskretnym (tj. automaty)

Def. System dynamiczny z czasem dyskretnym n-tego rzędu

Y(n+k) = f[y(n-1 + k), y(n-2 + k), …, y(k)]

Gdzie k=0,1,2

Swoją następną wartość czasie wyliczy, jeżeli ma n poprzednich wartości.n-1, n-2 itd.

Aby zacząć symulację (automat n-tego rzędu) trzeba znać n-poprzednich wartości to jest y(0), y(1),…, y(n-1)

Ciąg Fibonacciego

y(k+2) = y(k+1) + y(k) - równanie różnicowe

y(0) = 1 k=1, 2, 3…

y(1) = 1

po rozwiązaniu powyższego równania różnicowego otrzymuje się:

y(k) = A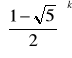
+B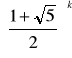

Stałe A i B wyliczamy z wartości początkowych

System dynamiczny - równanie liniowe

y(k+1) = ay(k)+b

y(0)=c

k=0, 1, 2, …

y(k) = a^k c + [a^k-1 + a^k-2 + … + 1] AK = c a^k + (1-a^k) b /(1+a^k)

Model pajęczyny

s=s_o + b p

d=d_o - a p

d(k+1) = d_o - ap(k+1)

s(k+1) = s_o + bp(k)

d(k+1)=s(k+1) - popyt dopasowuje się do podaży

p(k+1) = (d_o-s_o)/a + (- b/a) p(k) - równanie kształtowania się ceny

Czy istnieje cena równowagi ?

Cena równowagi p* musi spełniać w granicy (k ∞) równanie:

p*=(d_o-s_o)/a+b

p(k) = p(0) [ (-b/a)^k + (1-(b/a)^k )/( 1+(b/a)) * (d_o-s_o)/a]

dwa przypadki:

b<a b/a > 1 cena dąży do ceny równowagi (p*)

b>a b/a < 1 deregulacja rynku (rozregulowanie)

Genetyka

p(k) - frakcja cech A w generacji k-tej

q(k) - 1-p(k) - frakcja cech a w generacji k-tej

p(k+1) = ?

q(k+1) = ?

	p	q
p	p^2	pq
q=1-p	pq	q^2

Przestrzeń prawdopodobieństwa

Równianie Hardy-Heiberg'a - system dynamiczny

p(k+1) = (p²w₁₁ + pqw₁₂) / ( p²w₁₁ + 2pqw₁₂ + q²w₂₂) k = 0,1,2,…

q(k+1) = (q²w₂₂ + pqw₁₂) / ( p²w₁₁ + 2pqw₁₂ + q²w₂₂)

w_xy - współczynniki efektywności (prawdopodobieństwa efektywności skojarzenia)

Czy nie rozwiązując tych równań można znaleźć punkt stabilny ?

Punkty stabilności powyższego systemu:

1) p(0) = 0 p(k) =0 oraz q(k) = 1

2) q(0) = 0 q(k) =0 oraz p(k) = 1

Warunek największej efektywności (zbieżności Weinberg'a)

w_{12 >} w₂₂

w_{22 >} w₁₁

Przypadek specjalny doboru w_{11 ,} w_{12 ,} w₂₂ :

w₁₁ = w₁₂ = 1

w₂₂ = 0 (cecha regresyjna) takie dziecko się nie rodzi (?)

Wtedy otrzymujemy:

q(k) = (0 + (1-0)q) / ( (1-q)²*1 + 2(1-q)q + 0) = q / (1+q)

q(k+1) = q(k) / (1+q(k)) ,rozwiązaniem tego równania jest q(k) = 1/k

Systemy dynamiczne z czasem ciągłym

a) segment

b) 2 segmenty (koło siebie) - sklejanie segmentów

Definicja systemu dynamicznego

Definiuje się k zmienne dla każdego systemu. System jest dynamiczny jeśli:

Istnieje wektor stanu, istnieje operator F, istnieje operator G. Funkcje stanu dla czasu t dają się wyliczyć z G i F.

Dla takich t0 i t, że t>t0 :

z(t) = F [z(t) ; x_t0..t ] równanie dynamiki stanu

y(t) = G [z _t0 ; x_t0..t] równanie wyjścia

x_t0..t y

• Należy określić stan z(t).

• Za pomocą operatorów F,G znajdujemy stan wyjścia.

- Jeżeli operatory F i G są zwykłymi operatorami i pozwalają obliczyć wyjście to jest to system deterministyczny.

- System deterministyczny - tak samo przygotowany (czyli taki sam stan początkowy), jeśli dostaje takie samo wymuszenie, to daje zawsze taką samą odpowiedź. Np. nie jest to Totolotek, bo zawsze jest tak samo przygotowany, ale daje różne odpowiedzi.

- System dynamiczny jest stochastyczny gdy F lub G są operatorami stochastycznymi.

Własność, po której systemy dynamiczne można nazwać deterministycznymi (system deterministyczny nie zależy od sposobu jego opisania):

Dla każdych t₀ , t' , t takich, że t₀ < t' < t mamy:

F[ F[z(t₀) ; x_t0..t' ] ; x_t'..t ] = F [ z(t₀) ; x_t0..t, x_t'..t ]

Systemy dynamiczne stacjonarne

System statyczny - to system bez pamięci , system w którym zależność wyjścia od wejścia jest funkcyjna (brak pamięci poprzednich stanów)

y(t) = f(x(t))

Operator przesunięcia:

( x_t0..t ) = x_{t0 + τ .. t + τ}

Niestacjonarność systemu - sposób, w jaki system reaguje w zmiennym czasie. Dynamika w czasie jest niezależna od stanu początkowego.

Stan ustalony systemu dynamicznego - Jest to stan systemu, gdy t oo

System dynamiczny ciągły - system jest ciągły gdy stany początkowe dążą to t₀. Stany dążą do wymuszenia, to również reakcje systemu są zbieżne do stanu odpowiadającemu granicznym wartościom.

C(t)

locus

aminokwasy

t

C*

a

a

t

C_o

C(t)

C*''

C*'

t

1 2 3 4 5 6 7 8…

N_t (k)

β < 0

β = 0

β > 0

t

m_o

A

A

Podaż s_o

Popyt d_o

ds

p(k)

p(k+1)

P - cena

a

A

t₀

x_to-t = x(.) | _{[t0; t]}

x_t'..t . x_t0..t' = x_t0..t

t

Regresja urodzeń

q(k)

k

dzielność

w

w

0

punkt stabliny

1

punkt stabliny

p

punkt największej dzielności

t₁

x(.)

segment

t₀

x(.)

t'

t

x_t0..t'(.)

x_t'..t(.)

F, G, z(t)

---