Kaczor Łukasz 2005-11-13

Sprawozdanie z ćwiczenia nr 8

Pomiar momentu bezwładności za pomocą
wahadła Maxwella

1. Zagadnienia teoretyczne

Dynamika zajmuje się opisem ruchu ciał, objaśniają jednocześnie warunki oraz przyczyny, na skutek których ciął poruszają się lub pozostają w spoczynku. Prawa dynamiki ruchu obrotowego podaje się dla bryły sztywnej. Dowolne przesunięcie bryły sztywnej (tj. ciała, w którym odległość między punktami jest stałą, niezależnie od siły działającej na ciało; czyli ciała, którego kształt i wymiary pozostają niezmienne) można traktować jako jeden z dwu podstawowych rodzajów ruchu: postępowego i obrotowego lub ich złożenia. W ruchu obrotowym poszczególne punkty ciała zakreślają okręgi współśrodkowe, których środki leżą na linii prostej nie biorącej udziału w ruchu, zwanej osią obrotu. Drogi przebywane jednocześnie przez punkty położone w różnych odległościach od osi obrotu nie są równe, a więc punkty te mają różne prędkości liniowe.

Do opisu bryły sztywnej nie wystarczą pojęcia siły, pędu, czy masy. Należało wprowadzić takie wielkości, które połączą wyżej wymienione wielkości z odległością od osi obrotu. Takimi wielkościami są moment siły, moment pędu i moment bezwładności.

U podstaw dynamiki leżą zasady sformułowane przez Newtona. Poniżej podam zasady dynamiki dla ruchu obrotowego, z racji tego iż taki właśnie ruch jest badany w tym ćwiczeniu:

Pierwsza zasada dynamiki. Jeśli moment siły działającej na bryłę sztywną wynosi zero, to bryła sztywna pozostaje w spoczynku lub wykonuje ruch obrotowy jednostajny

Druga zasada dynamiki. Moment siły działającej na bryłę sztywną jest równy pochodnej momentu pędu względem czasu.

Trzecia zasada dynamiki. Jeśli na bryłę sztywną A działa bryła sztywna B pewnym momentem siły to bryła B działa na bryłę A momentem BA odwrotnym do momentu AB.

Zasada zachowania energii

Energia spełnia prawo, zwane zasadą zachowania energii, dotyczące całkowitej energii
E układu. Energia całkowita jest to suma energii mechanicznej układu, jako energii termicznej oraz wszystkich rodzajów jego energii wewnętrznej, innych niż energia termiczna. Zasada zachowania energii mówi, że zmiana całkowitej energii E układu jest równa energii dostarczonej do układu lub od niego odebranej.

Zasady zachowania energii nie wyprowadzono z podstawowych praw fizyki. Jest to prawo wynikające z niezliczonych doświadczeń.

Jeśli układ jest izolowany od otoczenia, to energia nie może być do niego dostarczona, ani od niego odebrana. Wiele zmian energii może natomiast zachodzić w obrębie układu izolowanego, na przykład energia kinetyczna może zamieniać się na energię potencjalną lub energię termiczną. Jednakże suma wszystkich rodzajów energii w układzie nie może ulegać zmianie.

Wyliczanie momentu bezwładności

Jeśli ciało sztywne składa się z kilku cząstek, to jego moment bezwładności względem pewnej osi obrotu można obliczyć ze wzoru

wyznaczając iloczyn mr² dla każdej cząstki, a następnie dodając te iloczyny do siebie. Jeśli ciało sztywne składa się z wielu blisko siebie położonych cząstek to do obliczenia momentu bezwładności może nam posłużyć wzór, który sumę w podanym równaniu zastępuje całką:

Jeżeli chcemy wyznaczyć moment bezwładności I ciała o masie m względem pewnej osi możemy skorzystać z twierdzenia Steinerali. Jeśli znany jest moment bezwładności I_SM tego ciała względem osi równoległej przechodzącej przez środek masy ciała. Oznaczając przez h odległość tych osi, moment bezwładności względem osi danej jest równy

2. Wykonanie ćwiczenia

1. Przyrząd podłączono do sieci i uruchomiono poprzez wciśnięcie W3.

2. Na krążek wahadła nałożono pierścień, poprzez dociśnięcie go do oporu.

3. Skręcono na osi wahadła nić zawieszenia i unieruchomiono ją za pomocą elektromagnesu ( poprzez wciśnięcie przycisku W2)

4. Po uregulowaniu wysokości wspornika dolna krawędź pierścienia pokrywała się
   z zerem skali naniesionym na kolumnę.

5. Przyrząd wyzerowano poprzez wciśnięcie przycisku W1, po czym wciśnięto przełącznik W2.

6. Odczytano zmierzoną wartość czasu spadania wahadła i wpisano ją do tabeli pomiarowej.

7. Pomiar powtórzono 10 razy w celu wyznaczenia wartości średniej, po czym wyżej wymienione czynności zostały powtórzone dla drugiego pierścienia.

m0 [kg]	mk [kg]	mp [kg]	d [m]	r0 [m]	rk [m]	rp [m]	h [m]	t [s]	Idoś [kg ∙ m^2]	Iteor [kg ∙ m^2]	∆ [%]
0,0325	0,124	0,389	0,00105	0,00495	0,043	0,0525	0,41	2,283	0,00082	0,00102	19,5
																			2,288
																			2,289
																			2,272
																			2,281
																			2,284
																			2,271
																			2,283
																			2,281
																			2,276
													0,259						2,195	0,00059	0,00072	17,9
																			2,198
																			2,226
																			2,202
																			2,227
																			2,196
																			2,230
																			2,196
																			2,205
																			2,205

3. Obliczenia

Dla pierwszego pierścienia masa m jest sumą masy wahadła m₀, masy krążka m_k i masy pierścienia nałożonego na krążek m_p. Zatem

m = m₀ + m_k + m_{p =} 0,0325 + 0,124 + 0,389 = 0,546 kg

Moment bezwładności wahadła Maxwella został obliczony z zależności:

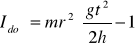
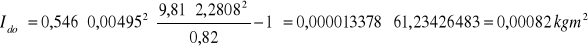
Wyliczam teoretyczny moment bezwładności

I_teor = 0,0000004 + 0,00011656 + 0,0008966 = 0,001017 kgm²

Dokładność pomiaru sprawdzam poprzez wyliczenie następującego wyrażenia

Dla drugiego pierścienia masa m jest sumą masy wahadła m₀, masy krążka m_k i masy pierścienia nałożonego na krążek m_p. Zatem

m = m₀ + m_k + m_p = 0,0325 + 0,124 + 0,259 = 0,417 kg

Moment bezwładności wahadła Maxwella został obliczony z zależności:

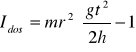
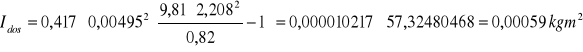
Wyliczam teoretyczny moment bezwładności

I_teor = 0,0000004 + 0,00011656 + 0,0005969 = 0,00071386 kgm²

Dokładność pomiaru sprawdzam poprzez wyliczenie następującego wyrażenia

I_doś1 = (0,00082 ± 19,5%) kg ∙ m²

I_doś2 = (0,00059 ± 17,9%) kg ∙ m²

4. Wnioski

Na podstawie przeprowadzonego ćwiczenia można zauważyć, że moment bezwładności wahadła Maxwella zależy od masy pierścienia nałożonego na wahadło. Podczas przeprowadzania ćwiczenia zaobserwowano, że im pierścień miał większą masę tym większy był czas jego opadania.

---