LICZBY ZESPOLONE
Definicja liczby zespolonej:
Liczbą zespoloną nazywamy uporządkowaną parę z=(x,y) liczb rzeczywistych, tj. x,y![]()
R.
Definicja równości, sumy i iloczynu liczb zespolonych:
Niech z1=(x1,y1) i z2=(x2,y2) będą liczbami zespolonymi. Definiujemy:
równość liczb zespolonych z1 i z2: z1=z2

x1=x2 ^ y1=y2dodawanie liczb zespolonych z1 + z2: (x1,y1)+(x2,y2)=(x1+x2,y1,y2)
iloczyn liczb zespolonych z1∙z2: (x1,y1)∙(x2,y2)=(x1+x2-y1,y2,x1y2+x2y1)
Definicja liczby przeciwnej:
Liczbę zespoloną postaci (-x,-y) nazywamy liczbą przeciwną do (x,y).
Definicja odejmowania liczb zespolonych:
Odejmowanie liczb zespolonych określamy wzorem: (x1,y1)-(x2,y2)=(x1,y1)+(-x2,-y2)=(x1-x2,y1-y2)
FAKT: Liczby zespolone postaci (x,0), gdzie x

R, mają następujące własności:
(x1,0)+(x2,0)=(x1+x2,0)
(x1,0)∙(x2,0)=(x1∙x2,0)
(x1,0)-(x2,0)=(x1-x2,0)
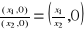
, gdzie x2
0
Z własności tych wynika, że zbiór ![]()
można utożsamiać ze zbiorem liczb rzeczywistych R. Stąd będziemy pisali x zamiast (x,0).
Definicja liczby odwrotnej:
Liczbą odwrotną do liczby zespolonej z=(x,y), z![]()
0, nazywamy liczbę postaci:
![]()
przy czym spełniony jest warunek: ![]()
.
Sprawdzenie:
z=(x,y)
![]()
Sprawdzamy, czy ![]()
![]()
c.n.d.
Definicja dzielenia liczb zespolonych:
Dzielenie liczb zespolonych z1 i z2 określamy wzorem:
![]()
Definicja jednostki urojonej:
Liczbę zespoloną postaci (0,1), ozn. symbolem i, nazywamy jednostką urojoną.
UWAGA: Jednostka urojona i ma tę własność, że i2=-1!!!
Sprawdzenie: i2=(0,1)∙(0,1)=(0∙0-1∙1,0∙1-1∙0)=(-1,0)=-1
UWAGA: postać algebraiczna liczby zespolonej:
Każdą liczbę zespoloną z=(x,y) można zapisać w postaci:
z=x+iy
nazywaną postacią algebraiczną liczby zespolonej.
Sprawdzenie: z=(x,y) (x,y)=(x,0)+(0,y)=(x,0)+(y,0)∙(0,1)=x+yi c.n.d.
Definicja części rzeczywistej i części urojonej:
Niech z będzie liczbą zespoloną postaci z=x+iy. Wówczas:
liczbę x nazywamy częścią rzeczywistą liczby zespolonej z, co zapisujemy: Rez=x
liczbę y nazywamy częścią urojoną liczby zespolonej z, co zapisujemy: Imz=y
Liczbę zespoloną postaci z=iy, gdzie y![]()
R\{0}, nazywamy czysto urojoną.
Definicja płaszczyzny zespolonej:
Każdej liczbie zespolonej z=x+yi odpowiada dokładnie jeden punkt o współrzędnych (x,y) na płaszczyźnie. Płaszczyznę, której punktom przyporządkowano liczby zespolone nazywamy płaszczyzną zespoloną, ozn. przez C, jej punkty nazywamy punktami płaszczyzny zespolonej.
Liczbom zespolonym postaci z=(x,0) odpowiadają punkty leżące na osi odciętych o współrzędnych z=Rez. Oś tę nazywamy osią rzeczywistą. Liczbom zespolonym postaci z=(0,y) odpowiadają punkty leżące na osi rzędnych o współrzędnych y=Imz. Oś tę nazywamy osią urojoną. Punkt (0,0) nazywamy zerem zespolonym.
oś urojenia
z1+z2
Imz=y
z1
z2
(0,0) Rez=x oś rzeczywista
zero zespolone
FAKT: Równość liczb zespolonych w postaci algebraicznej:
Dwie liczby zespolone z1 i z2 są równe wtedy i tylko wtedy, gdy ich części rzeczywiste są sobie równe, tj.: z1=z2![]()
Rez1=Rez2 ^ Imz1=Imz2.
FAKT: Działania na liczbach zespolonych w postaci algebraicznej:
Niech z1=x1+y1i oraz z2=x2+y2i :
dodawanie z1 + z2: z1+z2=(x1+x2)+(y1+y2)i
odejmowanie z1 - z2: z1-z2=(x1-x2)+(y1-y2)i
iloczyn z1∙z2: z1∙z2=(x1∙x2-y1∙y2)+(x1∙y2+x2∙y2)i -1
Sprawdzenie: z1∙z2=(x1+iy1)∙(x2+iy2)=x1x2+ix1y2+iy1x2+i2y1y2=(x1∙x2-y1∙y2)+(x1∙y2+x2∙y2)i
iloraz
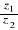
: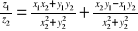
Definicja liczby sprzężonej:
Niech z=x+yi. Liczbę sprzężoną do liczby zespolonej z, oznaczamy symbolem ![]()
, nazywamy liczbę zespoloną postaci:
![]()
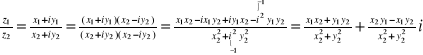
FAKT: Własności sprzężenia liczb zespolonych:
Niech z, z1 i z2![]()
C. Wtedy:
Dowód: z1=x1+iy1, ![]()
=x1-iy1, z2=x2+iy2, ![]()
=x2-iy2
![]()
c.n.d.
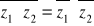
-1
Dowód: z1∙z2=(x1+iy1)∙(x2+iy2)=x1x2+ix1y2+iy1x2+i2y1y2=(x1x2-y1y2)+i(x1y2+y1x2)
L=![]()
=(x1x2-y1y2)+i(x1y2+y1x2) -1
P=![]()
=(x1+iy1)∙(x2+iy2)=x1x2+ix1y2+iy1x2+i2y1y2=(x1x2-y1y2)+i(x1y2+y1x2)
L=P c.n.d.
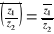
, o ile z2
0z+
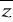
=2Rez
Dowód: z=+iy, ![]()
=x-iy
z+![]()
=x+iy+x-iy-2x=2Rez c.n.d.
z-
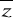
=2iImzz=
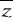

z=x
Rz

0
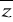

0Im
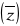
= -Im(z)
WNIOSEK:
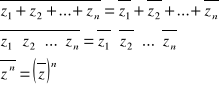
Definicja modułu liczby zespolonej:
Modułem liczby zespolonej postaci z=x+yi nazywamy liczbę rzeczywistą |z| określoną wzorem:
![]()
FAKT: Własności modułu liczby zespolonej:
Niech z, z1 i z2![]()
C. Wtedy:
|z| > 0
|z| = 0

z=0|-z|=|z|

=|z|z ∙
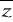
= |z|2
Dowód: z=x+iy, ![]()
=x-iy -1
z ∙ ![]()
=(x+iy)∙(x-iy)=x2-i2y2=x2+y2=![]()
=|z|2
|z1∙z2| = |z1| ∙ |z2|
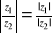
, o ile z2
0|z1+z2| < |z1| + |z2|
moduły
wartość bezwzględna
FAKT:
Dzielenie liczb zespolonych z1 i z2 wyraża się wzorem: ![]()
, o ile z2![]()
0.
Definicja argumentu i argumentu głównego liczby zespolonej:
Argumentem liczby zespolonej z= x+iy, z![]()
0, gdzie x,y![]()
R, nazywamy każdą liczbę φ![]()
R spełniającą układ równań:
Argument liczby zespolonej oznaczamy przez arg(z). Przyjmujemy dodatkowo, że argumentem liczby z=0 jest każda liczba φ![]()
R.
Argumentem głównym liczby zespolonej z![]()
0 nazywamy argument φ tej liczby spełniający nierówności: 0<φ<2π. Argument główny oznaczamy przez Arg(z). Przyjmujemy, że argumentem głównym liczby z=0 jest 0.
WNIOSEK: Każdy argument liczby zespolonej z![]()
0 ma postać arg(z)=Arg(z)+2kπ, gdzie k![]()
Z.
FAKT:
Niech z![]()
0 będzie dowolną liczbą zespoloną. Wtedy:
argument sprzężenia:
Arg![]()
=2π-Arg(z)
argument liczby przeciwnej:
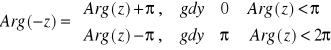
argument liczby odwrotnej:
Arg![]()
=2π-Arg(z)
POSTAĆ TRYGONOMETRYCZNA LICZBY ZESPOLONEJ
FAKT: Postać trygonometryczna liczby zespolonej:
Każdą liczbę zespoloną z=x+iy można przedstawić w postaci:
z = |z|(cosφ+isinφ) (1)
gdzie |z| oznacza moduł liczby zespolonej, a φ jej argument główny.
Wzór (1) nazywamy postacią trygonometryczną liczby zespolonej.
Dowód: z=x+iy
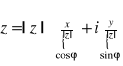
z=|z|(cosφ+isinφ) c.n.d.
Interpretacja geometryczna:
y=Imz
y z=x+iy
φ
x x=Rez
Przykład: Przedstawić w postaci trygonometrycznej liczby zespolone w postaci: z1=![]()
-i, z2=i,
z3=-3, z4=1+i
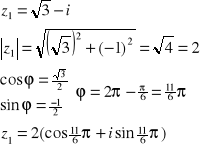

y=Imz y=Imz
1 z2
π
z3
1 x=Rez -3 -2 -1 x=Rez
y=Imz
1 z4
![]()
1 x=Rez
I ćwiartka |
φ0 |
II ćwiartka |
π - φ0 |
III ćwiartka |
π + φ0 |
IV ćwiartka |
2π - φ0 |
FAKT:
Liczby zespolone z1 = |z1|(cosφ1+isinφ1) i z2 = |z2|(cosφ2+isinφ2) są równe wtedy i tylko wtedy, gdy mają równe moduły i ich argumenty różnią się o całkowitą wielokrotność 2π, tj.:
|z1|=|z2| ^ φ1=φ2+2kπ, k![]()
Z
FAKT:
Niech z1 = |z1|(cosφ1+isinφ1) i z2 = |z2|(cosφ2+isinφ2) będą liczbami zespolonymi. Wówczas:
z1∙z2=|z1|∙|z2|∙[cos(φ1+φ2)+isin(φ1+φ2)] (2)
![]()
, o ile z2![]()
0
Dowód:
z1∙z2=|z1|(cosφ1+isinφ1)∙|z2|(cosφ2+isinφ2)= -1
=z1∙z2∙(cosφ1cosφ2+ cosφ1isinφ2+ isinφ1cosφ2+i2sinφ1sinφ2)=
= z1∙z2∙[cosφ1cosφ2- sinφ1sinφ2+i(cosφ1sinφ2+sinφ1cosφ2)]= |z1|∙|z2|∙[cos(φ1+φ2)+isin(φ1+φ2)]
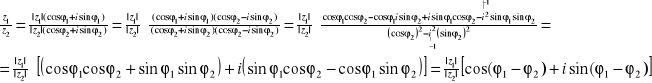
c.n.d.
UWAGA: Wzór (2) można uogólnić na dowolną liczbę czynników, tj.:
z1∙z2∙...∙zn=|z1|∙|z2|∙...∙|zn|∙[cos(φ1+φ2+...+φn)+isin(φ1+φ2+...+φn)]
FAKT: Wzór Moivre'a:
Niech z=|z|(cosφ+isinφ). Wówczas:
zn=|z|n∙(cosφ+isinφ)
Przykład: Obliczyć:
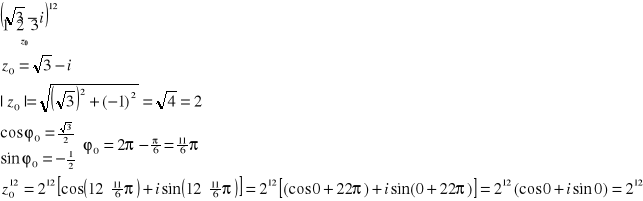
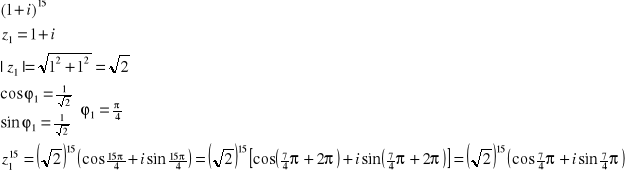
PIERWIASTKOWANIE LICZB ZESPOLONYCH
Definicja pierwiastka liczby zespolonej:
Pierwiastkiem stopnia n![]()
N z liczby zespolonej z nazywamy każdą liczbę zespoloną w spełniającą równość: wn=z.
Zbiór pierwiastków stopnia n z liczby zespolonej oznaczamy przez ![]()
.
FAKT: Wzór na pierwiastki z liczby zespolonej:
Każda liczba zespolona z = |z|(cosφ+isinφ) ma dokładnie n pierwiastków stopnia n. Zbiór tych pierwiastków ma postać:
![]()
gdzie:
![]()
(3)
dla k=0,1,2,...,n-1, przy założeniu, że φ jest dowolnym argumentem liczby zespolonej z.
WNIOSEK: Ze wzoru (3) wynika, że wszystkie pierwiastki z danej liczby zespolonej mają takie same moduły, a więc geometrycznie wszystkie leżą na okręgu o promieniu r=![]()
.
y=Imz
w2 w1 z
w3 w0
x=Rez
wn-1
![]()
Przykład: Wyznaczyć ![]()
z=-i
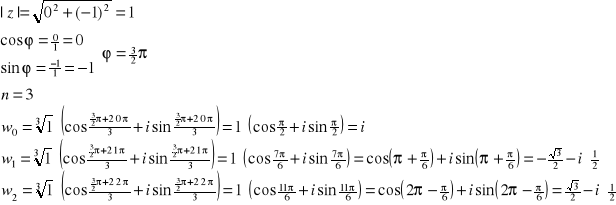
y=Imz
wo
α=β=γ
α β
γ x=Rez
w1 w2
Przykład: Wyznaczyć ![]()
z=-8+8![]()
i
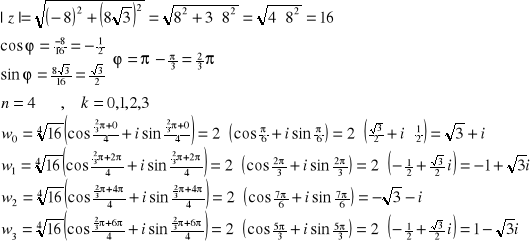
y=Imz
w1
w0
x=Rez
w2
w3
UWAGA: Jeżeli dla danej liczby zespolonej trudno jest wyznaczyć jej argument, wtedy jej
pierwiastek możemy wyznaczyć w sposób bezpośredni.
Metoda ta jest efektywna szczególnie w przypadku pierwiastka stopnia drugiego.
Przykład: Wyznaczyć ![]()
.
z=-6+8i
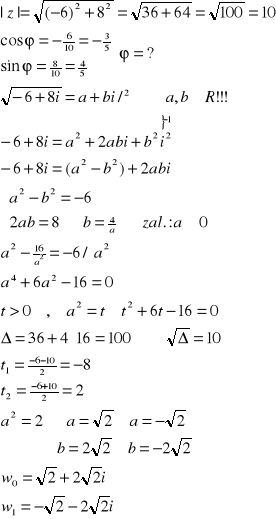
POSTAĆ WYKŁADNICZA LICZBY ZESPOLONEJ
Definicja symbolu eiφ:
Dla φ![]()
R liczbę zespoloną cosφ+isinφ oznaczamy krótko przez eiφ, tj. eiφ![]()
cosφ+isinφ.
FAKT: Własności symbolu eiφ:
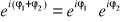
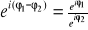
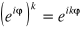
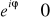
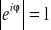
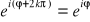
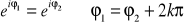
, gdzie k
Z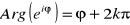
, dla pewnego k
Z
FAKT: Wzory Eulera:
Niech φ![]()
R. Wówczas zachodzą następujące wzory:
![]()
FAKT:
Niech ![]()
i ![]()
. Wówczas: z1=z2![]()
|z1|=|z2| ^ φ1=φ2+2kπ, k![]()
Z.
FAKT: Działania na liczbach zespolonych w postaci wykładniczej:
Niech ![]()
, ![]()
i ![]()
, gdzie φ1, φ2 i φ![]()
R, |z1|, |z2| i |z|>0, k![]()
Z.
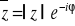
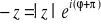
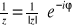
, o ile z
0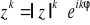
(wzór Moivre'a)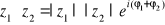
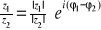
, o ile z
0
Przykład: Wykonać działania: ![]()
, jeśli ![]()
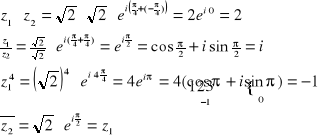
ROZWIĄZYWANIE RÓWNAŃ W ZBIORZE LICZB ZESPOLONYCH
Weźmy równanie:
zn+an-1zn-1+an-2zn-2+...+a1z+a0=0 (4)
o współczynnikach ai![]()
C, i=0,1,...,n-1, którego dziedziną jest zbiór liczb zespolonych.
Własność 1: Równanie (4) ma w zbiorze liczb zespolonych dokładnie n pierwiastków
(nieskończenie różnych)
Własność 2: Jeżeli liczba z0 jest pierwiastkiem równania (4) o współczynnikach rzeczywistych, tj.
ai![]()
R, i=0,1,...,n-1, to liczba zespolona ![]()
jest też pierwiastkiem tego równania.
Własność 3: Równanie (4) stopnia nieparzystego, o współczynnikach rzeczywistych ma, co
najmniej jeden pierwiastek rzeczywisty.
Przykład: Rozwiązać równania w płaszczyźnie zespolonej.
x2-2x+2=0
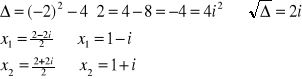
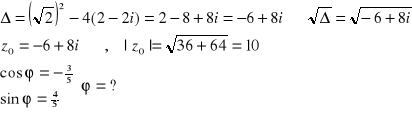
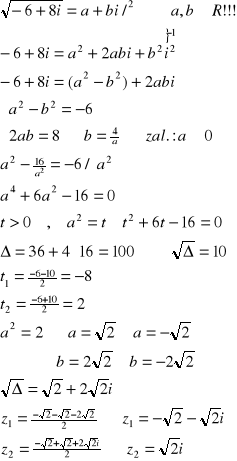
z5-z4+z-1=0
z4(z-1)+z-1=0
(z-1)(z4+1)=0![]()
z5=1
z4+1=0
z4=-1
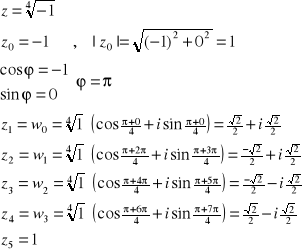
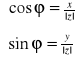
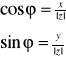
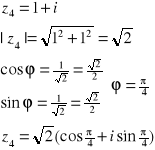
Wyszukiwarka