Ćwiczenie 12. Wyznaczanie napięcia powierzchniowego cieczy.

Wstęp:

Celem ćwiczenia jest wyznaczenie napięcia powierzchniowego cieczy tzn. wody destylowanej metodą rurki włoskowej i metodą wypływu kropel oraz wody destylowanej z detergentem, roztworu wodnego kwasu octowego i denaturatu metodą wypływu kropel.

Wyznaczanie:

Siły spójności to siły działające między cząsteczkami cieczy. Zasięg ich oddziaływań jest rzędu kilkudziesięciu średnic cząstek. W głębi cieczy, ze względu na równomierne rozłożenie cząstek, siły oddziaływań między cząsteczkami znoszą się wzajemnie. Na powierzchni cieczy jest jednak inaczej. Ponieważ gęstość nad cieczą jest mała, na cząsteczki w warstwie powierzchniowej działa wypadkowa siła spójności wywierana przez inne cząsteczki leżące głębiej. Jest ona zwrócona prostopadle do powierzchni cieczy. Przejawia się to tym, że ciecz dąży do zmniejszenia swojej powierzchni. Ciśnienie wywierana przez warstwę powierzchniową nazywa się ciśnieniem wewnętrznym cieczy.

W wyniku ciśnienia molekularnego, skierowanego w głąb cieczy w warstwie powierzchniowej występują siły cząsteczkowe leżące w płaszczyźnie tej warstewki - są to siły napięcia powierzchniowego. Gdy na długości „l” dowolnego konturu na powierzchni cieczy działa całkowita siła F, to napięcie powierzchniowe wynosi:

Napięcie powierzchniowe cieczy nie zależy od wielkości powierzchni, lecz od rodzaju cieczy i od jej temperatury. Dla wody w warunkach pokojowych wynosi ono
. Napięcie powierzchniowe wiąże się z pracą wykonaną wbrew siłom spójności, potrzebna do zwiększenia swobodnej powierzchni cieczy

Praca zużyta na zwiększenie powierzchni cieczy magazynowana jest w postaci energii powierzchniowej cieczy, nazywanej swobodną energią powierzchniową. Można ją ponownie zmienić na pracę:

Stąd mamy drugą definicję napięcia powierzchniowego:

Poza między cząstkowymi siłami przyciągania cieczy, występują też siły przyciągania lub odpychania między cząsteczkami cieczy i innych substancji. W wyniku istnienia tych sił obserwujemy zjawisko menisku, czyli uginania się powierzchni cieczy w pobliżu styku z naczyniem i związane z nim zjawisko włoskowatości - polegające na podnoszeniu się lub obniżaniu powierzchni płynu w wąskiej rurce.

Wykonanie ćwiczenia:

• Obliczamy promień kapilary na podstawie objętościowej podziałki na kapilarze

• Do czystego, szerokiego naczynia nalewamy wodę destylowaną

• Do wody wkładamy czystą kapilarę, którą zanurzamy głęboko, a następnie częściowo wynurzamy ją (pozostawiamy koniec kapilary w wodzie). Przed zanurzeniem należy kapilarę przedmuchać, aby nie było w niej wody.

• Za pomocą linijki mierzymy różnice poziomów wody w naczyniu i kapilarze.

• Pomiar wykonujemy trzykrotnie, średnią wysokość
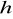
  podstawiamy do wzoru i obliczamy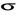
  wody.

Wyznaczanie napięcia powierzchniowego metodą wypływu kropel:

• Warzymy czyste i suche naczynko wagowe z pokrywą - masa
  .

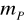
• Do czystej biurety z lejkiem wlewamy wodę destylowaną. Odkręcając kranik, wypuszczamy z biurety powoli 50 kropel wody do naczynka wagowego, przykrywamy je i ważymy wraz z zawartością. Obliczamy masę
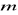
  jednej kropli wody.

• Pomiary opisane powyżej powtarzamy dla trzech cieczy.

• Obliczamy napięcie powierzchniowe badanych cieczy.

Obliczenia:

• Obliczam promień kapilary

• Obliczam średnią
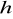
  wysokości słupa cieczy

• Obliczam napięcie powierzchniowe cieczy

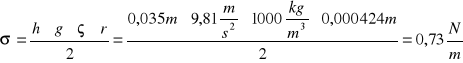
Pomiar metodą kroplową - obliczam masę jednej kropli:

• Woda destylowana

• Woda z detergentem

• Roztwór wodny kwasu octowego

• Denaturat

Obliczam napięcie powierzchniowe cieczy ze wzoru

• Wody destylowanej

• Wody destylowanej z detergentem

• Roztwór wodny kwasu octowego

• Denaturat

Rachunek błędu:

1. Pomiar za pomocą biurety

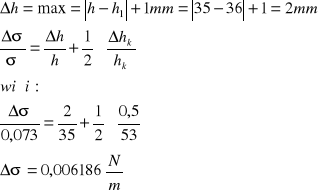
Obliczam błąd względny procentowy:

2. Pomiar metodą kroplową - roztwór wodny kwasu octowego

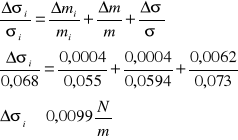
Obliczam błąd względny procentowy

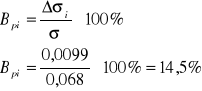
Wnioski:

Stosunkowo duży błąd wynikać może z niedokładności ważenia (niedokładne wytarcie naczynia, ewentualnego brudu na wadze, a także złego odczytania wysokości słupa wody - spowodowanym załamaniem się obrazu w szkle - kapilarze)

Błąd może również wynikać z nie sterylnych przyrządów zarówno mierników oraz naczyń, w których dane doświadczenie wykonywaliśmy.

---