EAIiE/EiT	Piotr Tuczapski	rok I	grupa IV	zespół 12
Pracownia fizyczna I	Drgania harmoniczne sprężyny			ćwiczenie 1
data wykonania 10.03.2005				ocena

Cel ćwiczenia:

Wyznaczanie współczynnika sprężystości i modułu sztywności drutu, z którego są zrobione.

Wprowadzenie:

Ruch harmoniczny zachodzi pod wpływem proporcjonalnej lecz przeciwnie skierowanej do wychylenia układu od stanu równowagi x siły F:

F=-kx

gdzie stała k to współczynnik sprężystości. Zależność wychylenia układu od czasu dla ruchu harmonicznego jest przedstawiona w następujący sposób:

x=Asin

gdzie A to maksymalna wartość wychylenia x - amplituda drgań, a wyrażenie w nawiasie - faza. T jest okresem drgań:

Stała k zależna jest od charakteru sił, pod wpływem których porusza się drgająca masa. Związana jest z ona z własnościami sprężystymi materiału np. modułem sztywności G, zależy również od wymiarów geometrycznych układu ( promień zwoju sprężyny R, promień r drutu, z którego została wykonana sprężyna i liczby zwojów n):

Wyprowadzając wzór
przyjęliśmy dwa założenia upraszczające. Nie uwzględniliśmy sił grawitacji jak również: masy sprężyny (ona również uczestniczy w drganiach). Rozpatrzmy kolejno wpływ obydwu czynników:

1) w przypadku nieważkiej sprężyny, na której zawieszono masę M , oprócz siły sprężystości działa siła ciężkości, tak że całkowita siła wynosi:

F= -kx + Mg

Zgodnie z II zasadą dynamiki otrzymujemy:

Ma= -kx + Mg

Ponieważ
, stąd:

M
+ -kx -Mg=0

Rozwiązanie tego równania różniczkowego ma postać:

gdzie:

zaś

Porównując z równaniem x=Asin
widać , że jest to ruch harmoniczny , zachodzący względem położenia
jakie przybierze masa M statycznie zawieszona na sprężynie.

2) w przypadku realnej sprężyny której masy m nie można zaniedbać wobec masy obciążnika M odpowiednie wyrażenie na T dane jest wzorem:

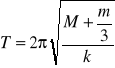
Zależność tę można otrzymać porównując energię kinetyczną ciężarka M: E=
i energię sprężyny m , której koniec ruchomy porusza się z tą samą prędkością v (punkt zaczepienia spoczywa). Rozpatrując element sprężyny o długości dx o masie dm=m
. Jego prędkość wynosi v(x)=v(
) . Zatem energia kinetyczna sprężyny dm wynosi:

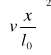
Całkowita energia kinetyczna sprężyny wynosi:

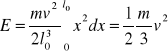
Całkowitą energię kinetyczną układu ciężarka i sprężyny wyraża zatem wzór:

.

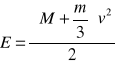
Prawo Hooke`a, Moduł Younga
Odkształcenie ciała stałego pod wpływem sił zewnętrznych polega na przemieszczaniu się cząsteczek (atomów) tego ciała z pierwotnego położenia równowagi w inne. Przemieszczeniu temu przeciwdziałają siły wewnętrzne ciała pochodzące od wzajemnego oddziaływania między cząsteczkami (atomami). Jeżeli przemieszczenie cząsteczek było niewielkie, to po usunięciu sił zewnętrznych, siły wewnętrzne przywracają cząsteczkom pierwotne położenie. Odkształcenie odpowiadające takiemu odwracalnemu przemieszczeniu cząsteczek nazywamy odkształceniem sprężystym. Jeżeli natomiast siła zewnętrzna przemieszcza cząsteczki ciała stałego tak znacznie, że siły wewnętrzne działające między cząsteczkami nie są zdolne do przywrócenia im położenia pierwotnego po usunięciu siły zewnętrznej, to odkształcenie nazywamy plastycznym lub trwałym.
Należy zaznaczyć, że przy długotrwałym działaniu nawet niewielkich sił zewnętrznych odkształcenie sprężyste może się stać odkształceniem plastycznym. Siły wewnętrzne działające między cząsteczkami odkształconego ciała stałego będziemy nazywali siłami sprężystości. Wypadkowa wszystkich sił zewnętrznych działających na ciało odkształcone jest równoważona właśnie przez siły sprężystości.

Wszystkie ciała wykazują charakterystyczny zakres odkształcenia, zwany elastycznością. Jeśli rozciągamy pręt (w kierunku osi x1), to relację miedzy przyłożonym naprężeniem σ11 i uzyskanym względnym wydłużeniem ciała ε11 opisuje słynne prawo Hooke'a:
	Prawo Hooke'a w jednym wymiarze (klasyczny test rozciągania)

Gdzie: E jest modułem Younga,
	(S - przekrój poprzeczny próbki),

Wyniki pomiarów i ich opracowanie:

1. Metoda statyczna wyznaczenia współczynnika sprężystości:

Po zważeniu poszczególnych obciążników wyznaczyłem statyczne wydłużenie sprężyny

Wyniki pomiarów zamieszczam w poniższej tabeli

Masa obciążnika [g]	Siła ciężkości [N]	Wychylenie sprężyny 1 [m]	Wychylenie sprężyny 2 [cm]
0	0	0	0
80,6	0,806	0,16	0,026
90,6	0,906	0,185	0,028
110,8	1,108	0,226	0,036
158,8	1,588	0,321	0,052
232,2	2,322	0,481	0,082
347,8	3,478	-	0,118
464	4,64	-	0,164
515,8	5,158	-	0,175

Po wykonaniu stosownych obliczeń otrzymałem

Współczynnik sprężystości k wynosi:
dla S1:	4,83
dla S2:	28,64

Błąd wartości k wynosi:
dla S1:
dla S2:

2. Metoda dynamiczna wyznaczenia współczynnika sprężystości:

1. Ważę obie sprężyny

Masa spręzyny wynosi:
dla S1:	88g
dla S2:	35,4g

2. Wprawiam sprężynę w ruch drgający o małej amplitudzie i dokonuję pomiarów

Masa obciążnika [g]	Masa układu drgającego z S1 [g]	Masa układu drgającego z S2 [g]	Okres drgań układu z S1 [s]	Okres drgań układu z S2 [s]	Kwadrat okresu drgań układu z S1 [s^2]	Kwadrat okresu drgań układu z S2 [s^2]
80,6	109,93	92,3	0,92	0,36	0,8464	0,1296
90,6	119,93	102,3	0,99	0,38	0,9801	0,1444
110,8	140,13	122,5	1,07	0,43	1,1449	0,1849
158,8	188,13	170,5	1,26	0,48	1,5876	0,2304
232,2	261,53	243,9	1,45	0,57	2,1025	0,3249
347,8	377,13	359,5	-	0,68	-	0,4624
464	493,33	475,7	-	0,82	-	0,6724
515,8	545,13	527,5	-	0,85	-	0,7225

Współczynnik kierunkowy prostej z wykresów (dany wzorem 4^2/k):
dla S1:	0,0082
dla S2:	0,0014
Odpowiednio współczynnik sprężystości k wynosi :
dla S1:	4,804878049
dla S2:	28,14285714

Błąd wartości k wynosi:
dla S1:
dla S2:

Porównując współczynniki sprężystości otrzymane metodą statyczną i dynamiczną można powiedzieć, iż mają one zbliżona wartość.

3. Wyznaczam moduł sztywności badanych sprężyn

Promień zwoju sprężyny [m]	Promień drutu [m]	Liczba zwojów sprężyny	Współczynnik sprężystości [N/m]	Moduł sztywności [N/m*m]
0,0014	0,00027	128	4,83	4,94685E-13	dla S1 w metodzie statycznej
0,0014	0,00027	128	4,8	4,91612E-13	dla S1 w metodzie dynamicznej
0,0005	0,00018	159	28,64	7,37709E-14	dla S2 w metodzie statycznej
0,0005	0,00018	159	28,14	7,2483E-14	dla S2 w metodzie dynamicznej

Błąd wartości G wynosi:
dla S1 w metodzie statycznej:
dla S1 w metodzie dynamicznej:
dla S2 w metodzie statycznej:
dla S2 w metodzie dynamicznej:

5

---