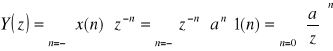
LABORATORIUM TEORII SYGNAŁÓW

Ćw. nr 6

TRANSFORMATA „Z” i TRANSMITANCJA

Tomasz GRZYŚKA

Gr. E1, sem. V

Sekcja 30

17.01.2001

1. Zadania do wykonania przed laboratorium.

1. Znajdź transformatę Z sekwencji:

y(n) = aⁿ 1(n)

gdzie: 1(n) jest dyskretnym skokiem jednostkowym.

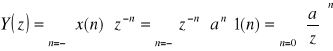
suma będzie zbieżna gdy:

stąd:

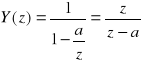
2. Znaleźć transformatę „Z” funkcji:

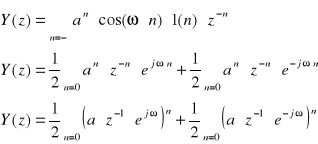
suma będzie zbieżna gdy:

i

tzn. wtedy gdy

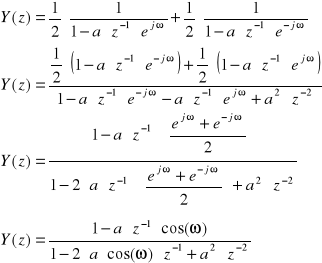
3. wyznaczyć transmitancję Z funkcji

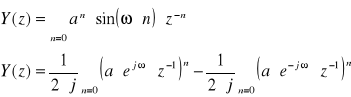
podany szereg będzie zbieżny gdy

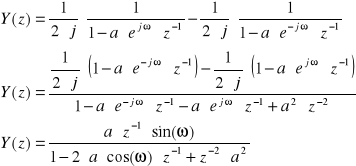
PROGRAM ĆWICZEŃ:

1. Splatanie eksponent.

1. Używając bloczka Convolve należy znaleźć splot dwóch sygnałów

y(n)=h(n)*x(n)

h(n) = aⁿ 1(n)

x(n) = bⁿ 1(n)

gdzie: a = 0,9

b = 0,5

Po wykonaniu operacji splotu otrzymujemy:

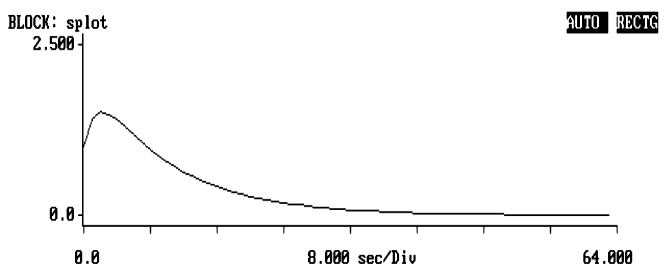
Maksimum dla 1,509.

2. Wyznaczamy splot sygnałów y(n) bez użycia bloczka Convolve.

W tym celu łączymy ze sobą bloczki IIR realizujące transmitancję H(z) i X(z).

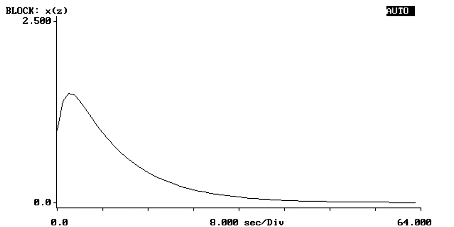
W wyniku takiej operacji otrzymujemy następujące widmo sygnału:

Maximum wynosi 1,51.

Z porównania obydwu widm można zauważyć że są identyczne. Można więc wywnioskować, że operacje splotu są równoważne (zamienne).

2. Odwrotna transformata „Z”

Dana jest transmitancja w postaci:

Należy znaleźć odpowiedź impulsową h(n).

Otrzymujemy poniższą odpowiedź na skok jednostkowy:

Przebieg z wykresu jest cosinusoidą. Wynika to z tego, że transmitancja filtru IIR H(z) jest transformatą „Z” sygnału
.

3. Tworzenie złożonych sygnałów.

Znaleźć szczytową wartość ciągów:

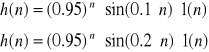
Transformata „Z” tych ciągów została wyliczona w przygotowaniu do ćwiczenia, należy teraz wyliczyć odpowiednie współczynniki a i b.

Dla pierwszego ciągu otrzymujemy :

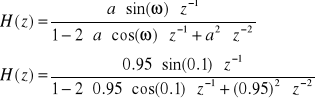
Odpowiedź na skok jednostkowy:

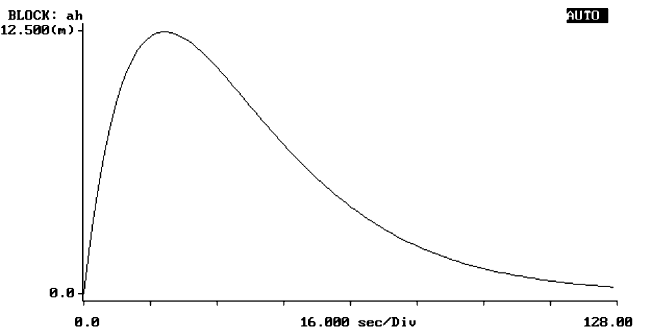
Dla drugiego ciągu otrzymujemy:

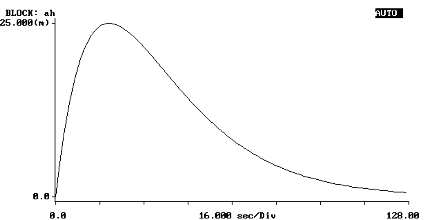
Odpowiedź na skok jednostkowy wynosi:

Szczytowa wartość pierwszego ciągu wynosi 1,244e-03

W drugim przypadku wartość szczytowa wynosi 2,500e-02

4. Równanie różnicowe.

Dla podanego równania różnicowego w postaci:

1. oblicz transmitancję
   

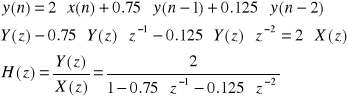
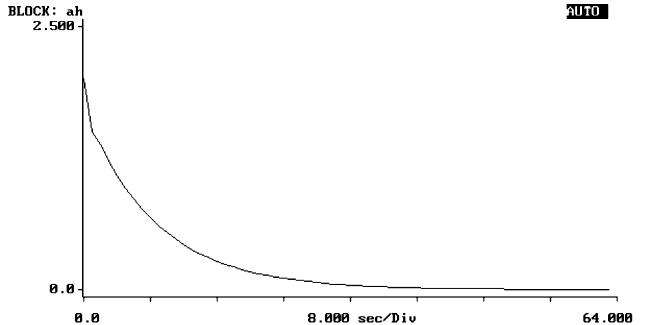
2. wyznaczyć odpowiedź impulsową h(n)

1

str. 7

---