Wykład 3
Przestrzeń Rn
Punkt przestrzeni n-wymiarowej będziemy oznaczać jedną literą ![]()
lub ![]()
.
Dla odróżnienia punktów używamy dodatkowego górnego wskaźnika ![]()
, ![]()
.
Odległość punktów ![]()
![]()
,![]()
określamy wzorem
![]()
.
Otoczenie i Sąsiedztwo w Rn
Niech r oznacza dowolną liczbę dodatnią, ![]()
ustalony punkt z ![]()
.
Otoczenie U(P0, r) punktu P0 o promieniu r jest zbiorem wszystkich punktów P, których odległość od punktu P0 jest mniejsza od r.
Inaczej zbiór ten nazywamy kulą o środku w punkcie P0 i promieniu r.
Sąsiedztwo S(P0, r) punktu P0 o promieniu r jest to zbiór wszystkich punktów P, dla których
![]()
.
Zatem
![]()
.
W ![]()
otoczenie U(P0, r) jest wnętrzem koła o środku w P0 i promieniu r.
W ![]()
otoczenie U(P0, r) jest wnętrzem kuli o środku w P0 i promieniu r.
Niech ![]()
Punkt PZ nazywamy punktem wewnętrznym zbioru Z, jeśli pewne otoczenie punktu P zawiera się w Z.
Zbiór punktów wewnętrznych zbioru Z nazywamy wnętrzem zbioru Z i oznaczamy intZ.
Punkt P nazywamy punktem brzegowym zbioru Z, jeśli w każdym otoczeniu punktu P znajduje się co najmniej jeden punkt należący do Z i co najmniej jeden punkt nie należący do Z.
Punkt P może należeć do Z lub nie. Zbiór punktów brzegowych zbioru Z nazywamy brzegiem zbioru Z.
Punkt P∈Z nazywamy punktem odosobnionym ( izolowanym ) zbioru Z, jeśli pewne sąsiedztwo punktu P jest rozłączne z Z.
Punkt P nazywamy punktem skupienia zbioru Z, jeśli w każdym sąsiedztwie punktu P znajduje się punkt należący do zbioru Z.
Zbiór Z nazywamy
- Otwartym, jeśli każdy punkt zbioru Z jest punktem wewnętrznym zbioru.
- Domkniętym, jeśli każdy punkt brzegowy zbioru Z należy do zbioru Z.
- Ograniczonym, jeżeli istnieje kula, w której zawiera się zbiór Z.
- Spójnym, jeśli dowolne dwa punkty zbioru Z można połączyć krzywą zawartą w zbiorze Z.
Zbiór otwarty i spójny nazywamy obszarem.
Obszar ze swoim brzegiem nazywamy obszarem domkniętym.
Def.
Ciąg punktów ![]()
![]()
przestrzeni ![]()
jest zbieżny do punktu x0 wtedy i tylko wtedy, gdy
![]()
.
Piszemy ![]()
lub ![]()
.
Tw.
Jeśli ![]()
![]()
, ![]()
to ![]()
![]()
.
Przykład 1
Naszkicować na płaszczyźnie kilka początkowych wyrazów ciągu ![]()
![]()
i wyznaczyć granice tych ciągów.
a) ![]()
, b) ![]()
.
Wskazać krzywe na których leżą wyrazy tych ciągów.
FUNKCJE WIELU ZMIENNYCH
Def:
Funkcją f n zmiennych ![]()
określoną w zbiorze ![]()
o wartościach w zbiorze R nazywamy przyporządkowanie każdemu punktowi ![]()
dokładnie jednej liczby rzeczywistej ![]()
.
Oznaczamy ![]()
lub ![]()
dla ![]()
Granica funkcji
Niech f będzie funkcją określoną w zbiorze ![]()
, niech x0 będzie punktem skupienia zbioru D.
Def:
Liczba g jest granicą funkcji f w punkcie x0,
co zapisujemy ![]()
jeżeli
według Heinego
dla każdego ciągu punktów 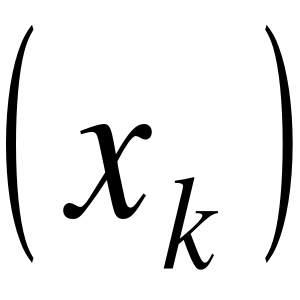
, ![]()
, ![]()
, zbieżnego do x0, ciąg ![]()
jest zbieżny do g.
według Cauchy'ego
![]()
.
Def:
Granicą funkcji f w punkcie x0 jest plus nieskończoność (minus nieskończoność),
co zapisujemy ![]()
jeżeli
według Heinego
dla każdego ciągu punktów 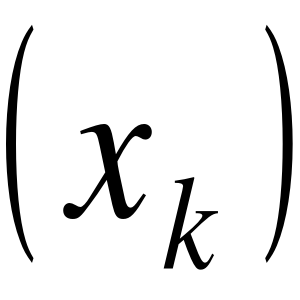
, ![]()
, ![]()
, zbieżnego do x0, ciąg ![]()
jest rozbieżny do ![]()
![]()
.zbieżny do g.
według Cauchy'ego
![]()
.
Przykład 2
Obliczyć granice
a) ![]()
, ![]()
b) 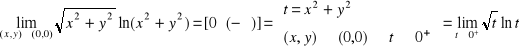
Wykazać, że nie istnieje granica funkcji ![]()
w punkcie ![]()
.
Wyszukiwarka