Opis układu pomiarowego
W ćwiczeniu wyznaczamy momenty bezwładności okrągłej tarczy metalowej o promieniu R=15 cm. Wzdłuż jednego z jej promieni rozmieszczonych jest 5 otworów, każdy w odległości 3 cm od poprzedniego. Umożliwia to równoległe przesuwanie osi obrotu tarczy o znaną wartość d. Tarczę mocuje się na balansowym sprężynowym mechanizmie obrotowym. Tarcza odchylona jest z położenia równowagi o kąt do 90° i puszczona swobodnie wykonuje drgania harmoniczne jak wahadło torsyjne.
Okres drgań tarczy wyraża się wzorem:
![]()
(42.11)
gdzie:
J - moment bezwładności tarczy względem zadanej osi obrotu,
D - stała zwana modułem skręcenia lub momentem kierującym zależna od budowy mechanizmu torsyjnego, w ćwiczeniu dla badanego układu D= 0,0255 Nm.
W ten sposób z pomiaru okresu drgań T można wyznaczyć moment bezwładności J. Stanowisko wyposażone jest w fotokomórkę, za pomocą której można automatycznie zmierzyć połowę okresu drgań, czyli T/2.
Wyniki pomiarów oraz ich średnie arytmetyczne
|
|
T/2 [s] |
|
|
|
STRONA: |
PRAWA |
LEWA |
|
PRZESUNIĘCIE OSI Z [CM] |
0 |
1,395 |
1,375 |
|
|
|
1,395 |
1,375 |
|
|
|
1,395 |
1,374 |
|
|
|
1,394 |
1,374 |
|
|
|
1,395 |
1,374 |
|
|
średnia: |
1,3948 |
1,3744 |
→1,3846 |
|
3 |
1,410 |
1,389 |
|
|
|
1,410 |
1,388 |
|
|
|
1,410 |
1,388 |
|
|
|
1,410 |
1,388 |
|
|
|
1,411 |
1,388 |
|
|
średnia: |
1,4102 |
1,3882 |
→1,3992 |
|
6 |
1,517 |
1,502 |
|
|
|
1,517 |
1,502 |
|
|
|
1,517 |
1,502 |
|
|
|
1,516 |
1,502 |
|
|
|
1,517 |
1,503 |
|
|
średnia: |
1,5168 |
1,5022 |
→1,5095 |
|
9 |
1,696 |
1,660 |
|
|
|
1,696 |
1,661 |
|
|
|
1,697 |
1,660 |
|
|
|
1,698 |
1,660 |
|
|
|
1,694 |
1,660 |
|
|
średnia: |
1,6962 |
1,6602 |
→1,6782 |
|
12 |
1,914 |
1,876 |
|
|
|
1,913 |
1,874 |
|
|
|
1,913 |
1,879 |
|
|
|
1,912 |
1,875 |
|
|
|
1,912 |
1,875 |
|
|
średnia: |
1,9128 |
1,8758 |
→1,8943 |
Niepewności standardowe
Wartość niepewności standardowej wyraża się wzorem:
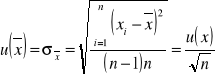
Obliczenia niepewności standardowych zostaną obliczone z dokładnością do 4 miejsc po przecinku. Działania rachunkowe zostaną wykonane na liczbach zaokrąglonych do 8 miejsc po przecinku.
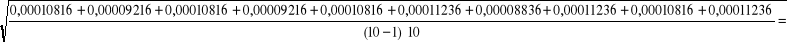
Dla d=0 cm
![]()
więc ![]()
0,0034
Analogicznie dla pozostałych d:
Dla d=3 cm
a) ![]()
b) ![]()
więc ![]()
0,0037
Dla d=6 cm
a) ![]()
b) ![]()
więc ![]()
00,24
Dla d=9 cm
a) ![]()
b) ![]()
więc ![]()
0,0060
Dla d=12 cm
a) ![]()
b) ![]()
więc ![]()
0,0062
Momenty bezwładności
Wychodząc z założenia 42.11: ![]()
i po przekształceniu wzoru otrzymujemy: ![]()
gdzie:
J - moment bezwładności tarczy względem zadanej osi obrotu,
D - stała zwana modułem skręcenia lub momentem kierującym zależna od budowy mechanizmu torsyjnego, w ćwiczeniu dla badanego układu D= 0,0255 Nm,
T - podwójna wartość zmierzonej średniej okresu drgań.
Moment bezwładności dla d=0 cm
![]()
Analogicznie dla wyznaczonej niepewności standardowej:
![]()
więc:
![]()
Moment bezwładności dla d=3 cm
![]()
Analogicznie dla wyznaczonej niepewności standardowej:
![]()
więc:
![]()
Moment bezwładności dla d=6 cm
![]()
Analogicznie dla wyznaczonej niepewności standardowej:
![]()
więc:
![]()
Moment bezwładności dla d=9 cm
![]()
Analogicznie dla wyznaczonej niepewności standardowej:
![]()
więc:
![]()
Moment bezwładności dla d=12 cm
![]()
Analogicznie dla wyznaczonej niepewności standardowej:
![]()
więc:
![]()
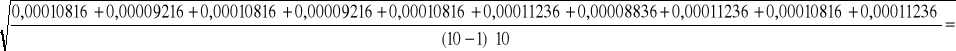
![]()
Wyszukiwarka