Ruch harmoniczny
W poprzednich rozdziałach poznaliśmy dwa rodzaje ruchu wynikające ze stałości (ruch postępowy) lub zmienności (ruch obrotowy) orientacji ciała w przestrzeni. Teraz zajmiemy się ruchem drgającym (drganiami) charakteryzującym się powtarzalnością położenia ciała w czasie. Szczególnym przypadkiem ruchu drgającego są drgania periodyczne charakteryzujące się powtarzalnością położenia w równych odstępach czasu (okres T).
S(t) = s(t+T)
kinematyka ruchu harmonicznego
Bardziej szczególnym przypadkiem jest z kolei ruch harmoniczny (drgania harmoniczne), w którym położenie ciała opisane jest przy pomocy funkcji sinus lub cosinus.
![]()
![]()
W równaniach tych x oznacza wychylenie z położenia równowagi trwałej, A amplitudę czyli maksymalne wychylenie z położenia równowagi trwałej, nawias nazywamy fazą Φ=ωt+ϕ, a prędkość kątowa ω=2π/T=2πf.
Rys. 21 Drgania harmoniczne
Rysunek 21 przedstawia koralik z masą m zamocowany dwoma sprężynami i wykonujący poziome drgania harmoniczne.
Podstawową własnością ruchu harmonicznego jest fakt, że na ciało wychylone z położenia równowagi trwałej działa siła o wartości proporcjonalnej do wartości wychylenia w tym samym kierunku i o przeciwnym zwrocie.
![]()
Zapisanie tego równania w postaci równania różniczkowego:
![]()
,
prowadzi do rozwiązania w postaci równania ![]()
. Obliczenie drugiej pochodnej tego równania i wstawienie jej do równania różniczkowego umożliwia powiązanie współczynnika „k” z masą i prędkością kątową.
![]()
![]()
![]()
![]()
Wykorzystując wzór na ω otrzymujemy:
![]()
,
lub:
![]()
![]()
.
Ostatni wzór jest godny zapamiętania gdyż wiele problemów z zakresu tej tematyki sprowadza się do wyznaczenia współczynnika „k” co umożliwia wyliczenie okresu drgań takiego ruchu. Z ostatniego wzoru wynika też, że ciało o większej masie charakteryzuje się większa wartością okresu drgań.
przemiany energii w ruchu harmonicznym
Powyżej wyliczono wzór na prędkość ciała w ruchu harmonicznym. Po wstawieniu go do wzoru na energię kinetyczną otrzymujemy:
![]()
.
Obliczmy teraz energię potencjalną powstałą wskutek pracy wykonanej przez siłę zewnętrzną równoważącą siłę harmoniczną [jako pole powierzchni pod wykresem F(x)].
Rys. 22 Energia potencjalna w ruchu harmonicznym
Wartość energii potencjalnej będzie równa wartości pola powierzchni zaznaczonego trójkąta:
![]()
.
Wstawiając podany wyżej wzór na wychylenie x otrzymujemy:
![]()
.
Całkowita energia mechaniczna w ruchu harmonicznym nie tłumionym (bez oporów) będzie równa:
![]()
.
W ostatniej linijce wykorzystaliśmy jedynkę trygonometryczną i uzyskaliśmy związek, z którego wynika, że energia mechaniczna w tym ruchu jest stała i równa maksymalnej energii kinetycznej lub maksymalnej energii potencjalnej. W ruchu tym mamy więc, podobnie jak w rzucie pionowym do góry zamiany energii kinetycznej w potencjalną i odwrotnie (rysunek 23).
Rys. 23 Przemiany energii w ruchu harmonicznym
składanie drgań harmonicznych
Ruch harmoniczny w wybranym kierunku możemy zastąpić ruchem rzutu końca wirującego wektora o długości równej amplitudzie na ten kierunek (rysunek 24).
Rys. 24 Konstrukcja wykresu wychylenia w funkcji czasu dla ruchu harmonicznego
Przyjmując do opisu ruchów harmonicznych wirujące wektory można w prosty sposób dokonywać składania takich ruchów odbywających się w jednym kierunku. Rysunek 25 przedstawia dwa takie drgania odbywające się odpowiednio fazami początkowymi: ![]()
i ![]()
oraz amplitudami: A1 i A2. Symbolicznie wirujące wektory odpowiadające poszczególnym drganiom oznaczono daszkami nad odpowiednimi symbolami.
Rys. 25 Składanie drgań harmonicznych odbywających się w tym samym kierunku
Z rysunku tego wynikają następujące zależności:
![]()
,
![]()
.
Z ostatniego równania można wyliczyć moduł (długość) wektora wypadkowego czyli amplitudę drgania wypadkowego lub cosinus różnicy kątów między nimi. Składowe amplitudy drgania wypadkowego i jej wartość bezwzględną można wyliczyć rzutując wektory wyjściowe na kierunki osi x i y oraz wykorzystując wzór na cosinus różnicy kątów.
![]()
![]()
![]()
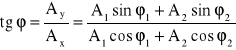
Innym szczególnym przypadkiem superpozycji (dodawania wektorowego) drgań jest składanie dwóch drgań wzajemnie prostopadłych. Jeśli w tym samym punkcie odbywają się drgania opisane równaniami:
![]()
,
![]()
,
to po podzieleniu tych równań stronami otrzymamy:
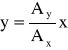
.
Jest to równanie prostej, a właściwie po uwzględnieniu maksymalnych wychyleń równych amplitudzie, równanie odcinka z dodatnim nachyleniem do osi ox. Gdyby przesunięcia fazowe różniły się o π to ze względu na własność funkcji sinus otrzymalibyśmy odcinek o ujemnym nachyleniu do osi x.
Jeśli dwa prostopadłe drgania różnią się amplitudami i fazą o nieparzystą wielokrotność ![]()
to otrzymamy zależności:
![]()
,
![]()
,
a stąd po wyliczeniu sinusa i cosinusa oraz wykorzystaniu jedynki trygonometrycznej:
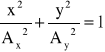
.
Ostatnie równanie jest równaniem elipsy o półosiach Ax i Ay. Jeśli przyjmiemy równość obu amplitud to otrzymamy równanie okręgu o promieniu równym wartości wspólnej amplitudy. Gdy stosunek częstości drgania pionowego do częstości drgania poziomego jest liczbą wymierną to jako drganie wypadkowe otrzymujemy tzw. krzywe Lissajous (patrz rozdział dotyczący prądów zmiennych).
drgania tłumione i wymuszone
Tłumienie jest zjawiskiem uważanym często za szkodliwy efekt oporów występujących w przyrodzie. Jednak są przypadki jego zbawiennego wpływu na maszyny używane przez człowieka. Jednym z bardziej znanych przykładów jest amortyzator samochodowy. Jakże zabawny widok przedstawiałaby „Syrenka” (albo 126p) po przejechaniu kilkuset metrów po polskiej drodze międzynarodowej. Jak trudno byłoby nie nabawić się „morskiej choroby”. Aby temu zapobiec stosuje się amortyzatory mające za zadanie wytłumić powstające drgania. Przykład charakterystyki czasowej takiego amortyzatora przedstawia górny wykres na rysunku.
Wynika z niego, że silne odkształcenie (przesunięcie koła w pionie) jest szybko kompensowane do wartości równej 0 nie przenosząc się w stronę przeciwną. Dolny wykres przedstawia przypadek słabego tłumienia, w którym drgania odbywają się z malejącą amplitudą.
Rys. 26. Drgania silnie i słabo tłumione
W przyrodzie bardzo ważnym zjawiskiem są drgania wymuszone a szczególny przypadek maksymalnego wzbudzenia nazywany rezonansem mechanicznym. W ogólności rezonans polega na uzyskaniu ekstremalnej wartości parametru związanego z przekazem energii drgań od czynnika wymuszającego (generator) do czynnika wymuszanego (odbiornika, rezonatora). W przypadku rezonansu mechanicznego uzyskuje się maksimum wzbudzenia objawiające się maksymalną wartością amplitudy drgań. Sytuację tą obrazuje poniższy rysunek, na którym oś pozioma jest osią częstotliwości ![]()
, ![]()
oznacza częstotliwość rezonansową odbiornika a A uzyskiwaną amplitudę drgań.
Rys. 27 Maksymalne wzbudzenie w rezonansie mechanicznym
Przykład rezonansu mechanicznego przedstawia kolejny rysunek. Wzbudzenie lewego wahadła matematycznego prowadzi do maksymalnego wzbudzenia wahadła o tej samej długości (z zatrzymaniem pierwszego) a potem do przeciwnego przekazu energii do wahadła pierwszego (itd.). Obserwuje się również drgania trzeciego wahadła o innej częstości własnej lecz ich amplituda jest niewielka.
Rys. 28. Rezonans mechaniczny wahadeł
Rezonans (mechaniczny i elektromagnetyczny) jest jednym z najważniejszych zjawisk fizycznych występujących w przyrodzie i wykorzystywanych w technice do przekazywania informacji (energii) w sposób selektywny.
Wyszukiwarka